
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Опорные инженерно-геодезические сети.Содержание книги
Поиск на нашем сайте
§1. РАСЧЕТ ТОЧНОСТИ СЕТЕЙ В ЗАВИСИМОСТИ ОТ КОЛИЧЕСТВА СТУПЕНЕЙ ИХ РАЗВИТИЯ.
На точность положения граничной точки земельного участка влияет не только выполнение геодезических измерений по ее координированию, но и точность геодезической опоры. Введем следующие предположения. Первое. Будем полагать, что исходной геодезической сетью для всех видов геодезических работ является государственная геодезическая сеть первого класса. На ее основе развивается сеть второго класса, третьего, четвертого. Сгущение государственной геодезической сети осуществляется сетями 1 и 2 разрядов. Координирование границ осуществляется теодолитными ходами, опирающимися на пункты опорных геодезических сетей (1 класс – 2 разряд). Все классы и разряды назовем общим термином – степени. Второе. При развитии геодезической сети последующего класса точности предусматривается привязка ее с обоих сторон (в начале и в конце) к пунктам сети высшего класса точности. Если обозначить через mi – среднюю квадратическую ошибку в положении наиболее слабоопределяемого пункта ступени i, mi-1 – ступени i – 1, а mизм. – среднюю квадратическую ошибку в положениях наиболее слабо определяемого пункта в ступени v, то можно записать, что m где k – коэффициент влияния ошибок положения пунктов ступени i – 1 на точность положения пунктов ступени i. В соответствии с результатом последних исследований k > 0,5. Если принять m1 – среднее квадратическое положение пункта 1 класса, то для средней квадратической ошибки второго класса будет: m Очевидно, что далее m m m m m6 соответствует средней квадратической ошибке положения наиболее слабо определяемого пункта второго (последнего) разряда, то есть последней седьмой ступени точности. Очевидно, что для нее выражение (6) в развернутом виде будет таким m Значение k находится в интервале [0.5; 1.0]. При этом нижний предел интервала соответствует наиболее благоприятному случаю влияния ошибок исходных положений пунктов, а верхний – наименее благоприятному. Если k принять равным для всей ступеней, что на этапе проектирования можно допустить, то формулу (7) для n-ступеней можно записать так m Если положить, что k=1, то m В наиболее благоприятном случае (k = 0.5) m При n=6 будет m Поскольку 0.54 = 0,06, то более высокими степенями можно пренебречь и записать: m а в общем случае m Если принять средний случай, то есть k = 0.75, то m Следуя инструкции о построении государственной геодезической сети СССР (М.: Недра, 1966) и инструкции по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500 (М.: Недра, 1985), mu можно принять одинаковым для каждого вида построения. Тогда для самого неблагоприятного случая в соответствии с (19). m2n = nm2u, (14) Для R = 0.5 по (12) m а для k = 0.7 по (13) m Обобщим теперь формулу (8). Расчет точности и числа ступеней развития опорных геодезических Сетей.
Введем следующие обозначения: mi – ср.кв. ошибка ступени с номером i; mi-1 – ср.кв. ошибка в положении наиболее слабого пункта в ступени i-1; mизм – ср.кв. ошибка пункта i-той ступени, вызванная ошибками выполняемых в ней измерений. Справедливым будет выражение m2i = k2m2i-1+m2изм. mu i = mизм. k – некоторый коэф., который устанавливается на основе научных исследований. m22 = k2m21+m2u2 mu2 – ср.кв. ошибка положения пункта, вызванная измерениями во второй ступени. m23 = k2m22+m2u3 = k2(k2m21+m2u2)+m2u3 = k4m21+k2m2u2+m2u3 m24 = k2m23+m2u4 = k2(k4m21+k2m2u2+m2u3) + m2u4 = k6m21+k4m2u2+k2m2u3+m2u4 Настоящие выражение можно обобщить для n – ступеней: m2n = k2n – 2m21 + k2n – 4m2u2 + k2n – 6m2u3 + k2n – 8m2u4 + … + m2un Приведем подобные в данном выражении, сделав следующие допущения m2u1 = m2u2 = … = m2un = m2u m2n = k2n – 2m21 + m2u(k2n – 4 + k2n – 6 + … + 1) В скобках – сумма членов геометрической прогрессии, в которой a1 = 1 – числитель q = k2 – знаменатель. В общем сумма членов геометрической прогрессии равна S = a1(qn– 1)/(q-1) S = 1(k2(n-1) – 1)/(k2 – 1) И, соответственно, получим m2n = k2n – 2m21 + m2u (k2(n - 1) – 1)/(k2 – 1) Исходя из этого выражения можно, задаваясь mn, m1, k, mu, рассчитать значения n, т.е. число ступеней и наоборот при известном числе ступеней, задаваясь другими значениями, можно определить k, mu
Рассмотрим частный случай Пусть опорная сеть развивается так
Мы имеем случай односторонней привязки, в этом случае К=1. Это самый неблагоприятный случай, но расчеты при нем будут гарантированны для всех случаев практики. При К стремящемуся к 1 найдем предел дроби:
(К^2(n-1) – 1)/(k²– 1); lim(k^2(n-1) – 1)/(k^2-1)
Мы получим неопределенность 0/0, для решения такой неопределенности применим правило Лопиталя, для этого продифференцируем числитель и знаменатель по К и найдем предел производных числителя и знаменателя, тогда будем иметь: lim(2(n-1)*k^(2(n-1)-1)/2k=n-1. То есть в самом неблагоприятном случае имеем простое выражение Mn^2= k^2(n-1) * m1^2 + mu^2 * (n-1) Однако мы имеем двустороннюю привязку всегда, при этом значение К, будучи меньше единицы, меньше 0,5 не бывает. Исследуем при каком значении n можно пренебречь ошибками исходных пунктов Mn^2=0.5^2(n-1) * m1^2 + mu^2 * (n-1) При n=2 0.5^2(n-1) =0.25, при n=3 0.5^2(n-1) =0.0625, при n=4 0.5^2(n-1) =0.0156 В технике принято, если одна из составляющих меньше другой в 10 раз, то ею можно пренебречь, Из этого следует, что ошибки исходных пунктов имеют существенное влияние лишь на 3-ю ступень развития опорной межевой сети. Другими словами при расчете точности геодезической сети следует учитывать ошибку лишь 2-х предыдущих ступеней.
§2. РАСЧЕТ ЧИСЛА И ТОЧНОСТИ СТУПЕНЕЙ ГЕОДЕЗИЧЕСКОЙ ОПОРЫ.
Для расчета числа и точности ступеней геодезической опоры воспользуемся формулой (9) самого неблагоприятного случая влияния исходных данных. В соответствии с ней средняя квадратическая ошибка наиболее слабоопределяемой точки в последней ступени определяется выражением: m где mi = mn. В предположении равенства между собой всех составляющих этого выражения получается формула (14). Однако если принять, что
для всех i, то можно записать что
Полагая, что m2 = km, То Соответственно В соответствии с (18) – (21) выражение (17) можно переписать так: m или m Находя в (23) общий знаменатель перепишем его так: m или m Исходя из этого выражения можно находить mo, n, mn и k в отдельности при заданных других величинах. Например, при определенном k, mn и mo можно вычислить n. Если задано mo, k, n, то можно вычислить mi. Действительно исходя из (17) m Очевидно, что в соответствии с (21)
Тогда m Полагая в (27) общий знаменатель k m Следовательно m или m В заключении отметим следующее. Во всех предыдущих выводах оценивалось лишь влияние ошибок положения исходных пунктов. Однако кроме этого влияние имеет место еще влияние ошибок исходных дирекционных углов. В наиболее неблагоприятном случае ошибки исходных дирекционных углов увеличивают дисперсии определяемых пунктов в последующей ступени в 2 раза. Следовательно, формулы (14), (12) и (13) можно записать так: m
§3. МЕТОДИКА РАСЧЕТА ТОЧНОСТИ ПРОЕКТА ГЕОДЕЗИЧЕСКОЙ СЕТИ.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.7.53 (0.011 с.) |

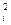 = k
= k  m
m  + m
+ m  , (1)
, (1) = k
= k 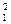 m
m  , (2)
, (2)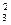 = k
= k 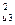 = k
= k  = k
= k  = k
= k  = k
= k  = k
= k  = k
= k 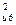 , (6)
, (6) = k
= k  m
m 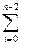 m
m  k2i, (8)
k2i, (8) , (9)
, (9)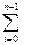 m
m  m
m 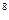 m
m 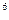 m
m  m
m  , (11)
, (11) + 0.25m
+ 0.25m  , (12)
, (12) + 0.31m
+ 0.31m  , (15)
, (15) Наиболее слабый пункт будет находится в последней ступени. Наивысшая точность измерения в первой ступени.
Наиболее слабый пункт будет находится в последней ступени. Наивысшая точность измерения в первой ступени.
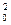 = m
= m  (18)
(18) (19)
(19)
 (20)
(20)
 (21)
(21) +
+  + … + m
+ … + m 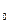 = m
= m 
 (23)
(23)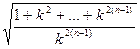 (24)
(24) (25)
(25)

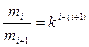

 +
+  + … + m
+ … + m 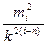 (27)
(27) запишем
запишем (28)
(28) (29)
(29)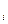 =
=  (30)
(30) + 2
+ 2  + … + 1).
+ … + 1).


