Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим теперь вынос проектных точек в натуру.Содержание книги
Поиск на нашем сайте
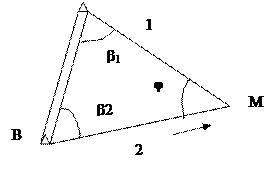
Существуют различные способы выноса проектных точек в плане. Наиболее распространенные среди них следующие: угловой засечки, линейной, способ полярных координат, прямоугольных координат, обхода, редуцирования Угловая засечка. Для выноса в натуру точки и в опорной точке А (рис. 30) откладывается проектный угол β1 и вдоль полученного направления фиксируется точка 1.
Рис. 30
В точке В откладывается угол β2 и фиксируется точка 2. Наблюдатель передвигается в створе линии В2 до тех пор пока не станет в створе линии А1. В пересечении створов фиксируется точка М. Линейная засечка.
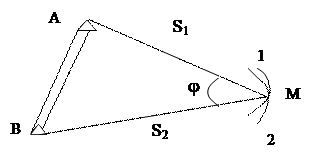
Рис. 31
В способе линейной засечки из точки А радиусом S1 прочерчивается на местности кривая 1. Из точки В радиусом S2 – кривая 2. При пересечении этих двух кривых фиксируется точка М.
Способ полярных координат. В точке А (рис 32) откладывается угол b1. Вдоль полученного направления откладывается расстояние S1 и фиксируется точка М.
Рис. 32 Способ прямоугольных координат.
В створе AA’ здания на расстоянии y ставят точку K1, В створе BB’ ставят точку K2 на расстоянии y. В створе K1 K2 ,на расстоянии x фиксируют точку K Контроль: если здание длиной l, то измеряется расстояние (l-x): (l-x) – (l-x)изм. ≤ 2mt y – yизм. ≤ 2mt
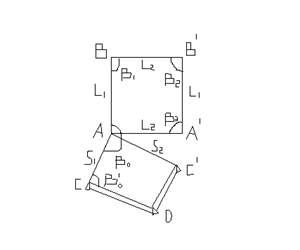
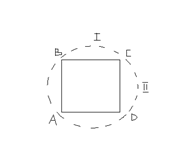
Способ обхода Этим способом выносятся главные проектные оси. Относительно опорных точек СDС ׳ выносится в натуру начальная точка А оси здания.
В точке A откладывается угол β0 и проектное расстояние L1. В точке B откладывается угол β1и проектное расстояние L2 В точке B’ откладывается угол β2 и проектное расстояние L1. В точке A’ откладывается. угол β3 и проектное расстояние L2. Мы должны замкнуться в точке А. Допуск незамыкания определяется СНИПом по монтажу конструкции. Средняя квадратическая ошибка монтажа не должна превышать 1 см, предельная ошибка не превышает 2см. Замечание В способе обхода вынос в натуру по полному контуру делать нельзя. Здесь вынос делают к средней точке объекта, по ходовой линии 1 и по ходовой линии 2. Средней в данном примере является точка С относительно точки А. Нестыковка осей не должна превышать допуска СНиП. Для здания это ± 2 см. Для границ городских земельных участков ± 20см.
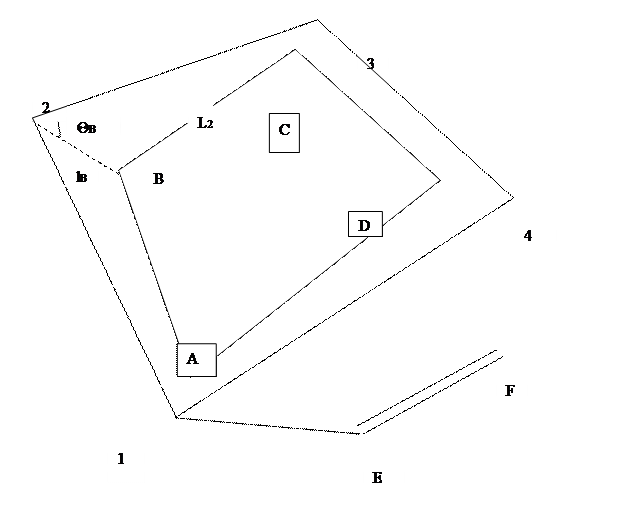
Частным случаем способа обхода является способ редуцирования. В этом случае вокруг объекта прокладывается теодолитный ход. Вычисляются координаты опорного теодолитного хода:. x1y1, x2y2 … xnyn, задаются проектными координатами объекта:xAyA, xByB … xA’yA’ Проектные точки выносятся в натуру относительно опорных (1,2,3,4) по элементам редукции. Элементами редукции точки В являются: lB и θB lB=√((X2-XB)2+(Y2-YB)2) θB = α2B – α23 α23 = arctg (y3-y2)/(x3-x2) α2B = arctg (yB-y2)/(xB-x2)
выноса в натуру являются промеры расстояний по осям объекта. Их сравнивают с вычисленными по проектным данным.Должно выполняться следующее условие: | l2 – l2выч | < 2mt
Для расчета точности отложения углов и линий при выносе точек в натуру используется следующие формулы. Точность определения положения пунктов прямой угловой засечки выражается следующей зависимостью:
где mb - средняя квадратическая ошибка измерения углов b1 и b2. r=3438¢ Из формулы можно найти точность отложения углов mb при выносе проектной точки в натуру.
В случае линейной засечки
Полагая mS1=mS2=mS можно найти
Если положить, что
то принимая
получим
и
В случае полярных координат
полагая
находят
и соответственно
§4. ВЫНОС В НАТУРУ ПРОЕКТНЫХ УГЛОВ И РАССТОЯНИЙ.
Рис. 33
Для выноса в натуру проектного угла β теодолит устанавливается в точке А. Наводят его на точку В и снимают отсчет а. Прибавив к этому отсчету значение проектного угла β и получится отсчет b = a + β, Теодолит поворачивают до тех пор, пока в отчетном приспособлении не появится отсчет b. После этого в перекрестии сетки нитей на местность фиксируется точка Nл. Индекс л обозначает, что все действия выполнялись при круге лево. Труба переводится через зенит и при другом круге, например, круге право, повторяются все описанные выше действия (наведение на точку В, снятие отсчета а, вычисление b). Фиксируется на местности вторая точка – Nn. В идеальном случае она должна совпадать с точкой Nл. В противном случае середина отрезка Nл, Nn фиксируется точка N, соответствующего направлению проектного угла β. При выносе в натуру проектного расстояния на местности откладывают наклонную длину D (рис. 34), соответствующую проектному горизонтальному расстоянию S.
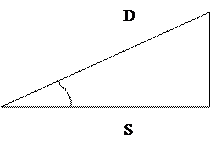 Рис. 34 Рис. 34
При этом наклонная длина определяется по формуле
где угол наклона υ определяется на местности. Значение наклонной длины определяется еще и по формуле D = S + ∆S, где
Вынос в натуру проектной точки по высоте. Вынос в натуру проектной точки по высоте включает две задачи: 1. Вынос в натуру проектной отметки. 2. Вынос в натуру проектного уклона.
Пусть необходимо вынести в натуру Н проектную, соответствующую насыпи дорожного полотна. Даны: НRp, Нпр. Найти: bпр. Необходимо найти отсчет bпр, установить его на местности движением рейки и на уровне пятки рейки зафиксировать точку. В строительстве эти точки закрепляются столбами. Наводим на репер и снимаем отсчет а по рейке, вычисляем Гп(горизонт прибора) ГП = НRp + а откуда следует, что bпр = ГП - Нпр . Движением рейки вверх – вниз добиваемся отсчета bпр и на уровне пятки рейки фиксируем точку. Иногда ставят рейку на землю, снимают отсчет b. r = b - bпр . И в данном месте закапывают столб высотой r.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1062; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.38.137 (0.007 с.) |


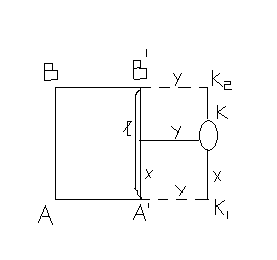
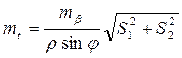
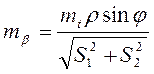
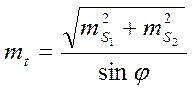
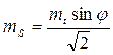
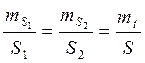
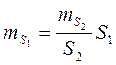
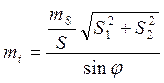
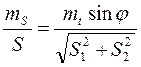
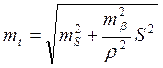
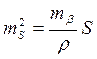
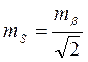
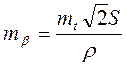
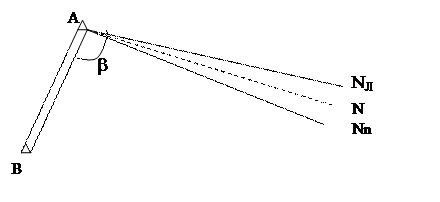
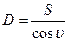
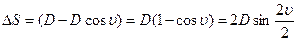 .
.