
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические характеристики поперечныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
А.Н. Дудченко
Практикум по сопротивлению материалов
Новочеркасск 2005 УДК 539.3/4 (076.5) ББК 30.121 я73 Д81 Рецензенты: д–р техн. наук, проф. П.Д. Кравченко, канд. техн. наук, доц. А.И. Резниченко
Дудченко А.Н.
Д 81 Практикум по сопротивлению / Юж.-Рос. гос. тех. ун-т. – Новочеркасск: ЮРГТУ, 2005. – 114 с. Рассмотрены шесть тем сопротивления материалов, по которым разработаны варианты домашних заданий и приведены примеры расчётов с подробными методическими указаниями. Предложены тестовые экзаменационные вопросы по 10 главам теоретического курса. Пособие предназначено для студентов 2 – 3-х курсов дневной и вечерней форм обучения специальностей “Технология машиностроения”, “Оборудование и технология сварочного производства”, “Котло- и реакторостроение”, “Промышленное и гражданское строительство” и др. Оно может быть также полезно студентам заочной формы обучения, испытывающим определённые трудности при освоении теоретического курса сопротивления материалов.
УДК 539.3/4 (076.5)
© Волгодонский институт ЮРГТУ, 2005 © Дудченко А.Н., 2005 ПРЕДИСЛОВИЕ Я слышу – я забываю. Я вижу – я запоминаю. Я делаю – я понимаю! Китайская пословица Учебные планы технических специальностей претерпели в последние годы значительные изменения, при этом существенно сократилось число аудиторных часов, выделяемых на изучение курса “Сопротивление материалов” на лекциях, практических и лабораторных занятиях, и сделан акцент на самостоятельную работу студентов при освоении учебного материала. С другой стороны, важность качественной подготовки инженеров в области прочностных расчётов несомненна, на что указывают продолжающиеся в стране техногенные аварии и катастрофы, вызванные ошибками проектирования, строительства и эксплуатации машин, зданий и сооружений. В этой связи возникает настоятельная необходимость в разработке учебно-методических материалов, способствующих развитию навыков самостоятельной работы студентов с целью ознакомления с проблемами прочности и методами их решения, а также закреплению теоретических знаний путём выполнения домашних заданий. Наряду с вышеизложенным наметилась тенденция к изменению методов проверки знаний студентов от традиционной формы контроля с выводами теоретических формул и углублённым пониманием всего комплекса осваиваемой дисциплины к принятой в большинстве стран рейтинговой, кредитно-модульной, тестовой форме контроля, облегчающей получение квалификационной оценки и формализующей ознакомительный подход студентов к прорабатываемому материалу.
В предлагаемом практикуме рассмотрены отдельные разделы сопротивления материалов, по которым согласно рабочим программам предусмотрены индивидуальные домашние задания на следующие темы: геометрические характеристики поперечных сечений стержней; статически неопределимые стержневые системы при растяжении-сжатии; плоский изгиб балок; расчёт балок методом начальных параметров; расчёт статически неопределимых рам методом сил; внецентренное сжатие неоднородных составных стержней. Все задания предваряются теоретическим материалом, необходимым и достаточным для осознанного решения предлагаемых задач. Рассмотренные примеры расчёта сопровождаются подробными методическими указаниями по их выполнению, при этом особое внимание уделено поэтапному контролю правильности решения и путям поиска возможных ошибок и их исправлению. Имея на руках практикум, каждый студент способен самостоятельно выполнить в домашних условиях индивидуальные задания и только в редких случаях ему потребуется дополнительная консультация и помощь преподавателя. Защита заданий также не вызовет больших затруднений, поскольку контрольные вопросы не выходят за рамки изложенного материала. Для облегчения подготовки к экзамену в практикуме публикуются 355 контрольных вопросов, на которые необходимо обратить внимание при проработке конспекта лекций и на основе которых составлены проверочные тесты, включающие в себя 10 выборочно взятых вопросов с пятью ответами (из них только один правильный). В зависимости от числа правильных ответов (0 – 10) уровень теоретической подготовки оценивается по десятибалльной шкале от отсутствующих знаний (0 баллов) до исключительных знаний (10 баллов).
Геометрические характеристики поперечных Сечений стержней Прочность, жёсткость и устойчивость деталей машин и элементов инженерных сооружений зависит в основном от внешних нагрузок, вида материала и размеров деталей и элементов, называемых в сопротивлении материалов стержнями. Условие прочности стержня можно записать в следующем виде:
где Параметр
где Влияние формы и размеров поперечного сечения на прочность, жёсткость и устойчивость обладает большой нелинейностью и выражается в виде особых геометрических характеристик. На рис. 1.1 показано поперечное сечение стержня, отнесенное первоначально к вспомогательной произвольно выбранной системе координат XOY. Вводятся следующие понятия, связанные с геометрией сечения:
где А и dA – площадь и дифференциал площади поперечного сечения; x, y, ρ – координаты дифференциала площади. В сопротивлении материалов все расчётные формулы получены с использованием главных центральных осей инерции U и V, положение которых определяется следующим образом. Вычисляются координаты центра тяжести сечения во вспомогательной системе координат XOY (рис. 1.1):
Рис. 1.1. Поперечное сечение стержня Находятся моменты инерции относительно центральных осей XC, YC, параллельных исходным осям X, Y (рис. 1.1):
Определяется значение угла
Вычисляются значения главных осевых и центробежного моментов инерции сечения
Для простых фигур (прямоугольника, треугольника, круга и т.д.) и широко используемых в практике составных фигур (двутавров, швеллеров, уголков и т.д.) все геометрические характеристики вычислены и представлены в справочниках в виде формул или таблиц сортамента (приложение). Проектируемые детали машин и элементы инженерных сооружений имеют разнообразные профили, которые можно разбить на составляющие с известными геометрическими характеристиками относительно их собственных центральных осей. В этом случае используются формулы для координат центра тяжести и моментов инерции составных фигур
где Рассмотрим кратко основные свойства геометрических характеристик. Единицы измерений: [ x, y, xC, yC, a, b ] = 1 м (1 см; 1 мм); [ A ]=1 м2 (1 см2; 1 мм2); [ SX, SY ] = 1 м3 (1 см3; 1 мм3); [ JX, JY, JXY, JP ] = 1 м4 (1 см4; 1 мм4). Знаки: площадь А, осевые JX, JY и полярный JP моменты инерции могут быть только положительными. Координаты х, у, хC, уC, а, b, статические моменты площади SX, SY и центробежный момент инерции JXY могут быть положительными, отрицательными и равными нулю.
Статические моменты площади SXC, SYC относительно осей, проходящих через центр тяжести сечения, всегда равны нулю – основное свойство центральных осей. Центробежный момент инерции JUV относительно главных осей всегда равен нулю – основное свойства главных осей. Относительно главных осей моменты инерции JU, JV экстремальны, т.е. один из них принимает максимальное значение, а другой минимальное – определение понятия “главные оси инерции”. При повороте осей координат на любой угол 1.1. Варианты и исходные данные домашнего задания № 1
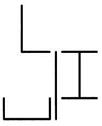
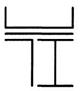
На рис. 1.2 приведены схемы компоновки поперечных сечений стержней из 4 прокатных элементов: листа, двутавра, швеллера, уголка. Зазоры между элементами показаны условно (при изготовлении стержней элементы прикладывают вплотную и соединяют путем сварки). Вариант задания (№ схемы) выбирают согласно списочному номеру студента в журнале преподавателя. Исходные данные, включающие в себя номера прокатных профилей и толщину листа, выбирают из табл. 1.1 согласно шифру – двум последним цифрам зачётной книжки студента.
Рис. 1.2. Компоновочные схемы поперечных сечений стержней
Таблица 1.1 Номенклатура прокатных профилей
а – первая цифра шифра; б – вторая цифра шифра.
Все размеры и собственные геометрические характеристики двутавра, швеллера и уголка выписывают из таблиц сортамента, приведенных в приложении. Ширину листа (больший из 2 размеров прямоугольника) определяют согласно компоновочной схеме сечения. Геометрические характеристики сечения листа вычисляют по формулам для прямоугольника.
1.2. Условие задания Для заданного составного сечения стержня вычислить главные центральные моменты инерции и моменты сопротивления. Сравнить прочность и жёсткость балки с заданным сечением при её плоском изгибе в 2 главных плоскостях инерции.
Пример расчёта и методические указания Подготовка исходных данных и расчетной схемы Решение задачи начинаем с выбора компоновочной схемы по номеру варианта и номенклатурных данных о фигурах прокатных профилей в соответствии с шифром (рис. 1.3). Порядковые номера фигур на схеме сечения задаём в любой последовательности. Ширину листа определяем согласно рис. 1.3:
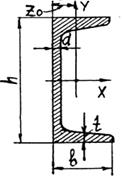
Рис. 1.3. Компоновочная схема сечения Изображаем эскизы “простых” фигур и показываем их основные размеры и центральные оси (рис. 1.4). Эскизы двутавра, швеллера и уголка располагаем согласно сортаменту прокатной стали (табл. 1 – 3), эскиз листа показываем так, как он расположен в компоновочной схеме (рис. 1.3). Выписываем из таблиц сортамента те значения размеров и геометрических характеристик, которые потребуются в дальнейших расчётах (рис. 1.4). Необходимо обратить внимание на вычисление моментов инерции прямоугольника: формулы JX = bh 3/12; JY = b 3 h/ 12 справедливы, если b ‖ х и h ‖ y. Центробежный момент инерции JXY фигуры равен нулю, если хотя бы одна из осей инерции (X или Y) является осью симметрии фигуры. Чертим сечение стержня в масштабе, используя компоновочную схему (рис. 1.3) и размеры “простых” фигур (рис. 1.4). Разрешённый масштаб (1:1; 1:2; 1:2,5; 1:4) выбираем с таким расчётом, чтобы поперечное сечение и вспомогательные построения разместились на листе формата А4 (рис. 1.5). И всего поперечного сечения Выбираем произвольную правовинтовую систему координат XOY и из центра тяжести каждой “простой” фигуры Сi проводим собственные центральные оси XCi, YCi, параллельные осям Х, Y. Показываем координаты центров тяжестей каждой фигуры хCi, yCi относительно вспомогательной системы XOY и вычисляем их значения, используя характерные размеры элементов с учётом их расположения в сечении (рис. 1.5):
Рис. 1.4. Эскизы фигур и их характеристики Определяем координаты центра тяжести поперечного сечения в системе осей XOY по формулам (1.3):
Рис. 1.5. Поперечное сечение стержня (М 1:2) Откладываем в масштабе отрезки хC, уC и проводим центральные оси ХС, YС, на пересечении которых получаем центр тяжести сечения С (рис. 1.5). Вычисляем координаты центров тяжестей “простых” фигур относительно центральных осей всего сечения XC, YC, используя формулы
Проверяем выполнение основного свойства центральных осей, для которых статические моменты площади должны равняться нулю:
Учитывая малую погрешность вычислений, заключаем, что координаты центра тяжести поперечного сечения найдены верно (при условии, что правильно определены координаты xCi, yCi).
Инерции сечения Используем формулу (1.1):
Так как угол получился отрицательным, откладываем его по ходу часовой стрелки и проводим главные оси U и V (рис. 1.5). Вычисляем значения тригонометрических функций
Проверяем основное тригонометрическое тождество
Инерции сечения Используем формулы (1.2):
Проверяем правильность вычислений. А. Условие стационарности суммы осевых моментов инерции при повороте осей: JXC + JYC = 4916+2602 = 7518 Б. Условие экстремальности главных осевых моментов инерции: JU = 5624 > { JXC = 4916 ∩ JYC = 2602} – максимум; JV = 1894 < { JXC = 4916 ∩ JYC = 2602} – минимум. В. Основное свойство главных осей: Выше мы вычислили
Относительно главных осей Осевые моменты сопротивления характеризуют изгибную прочность стержней (балок) с заданными геометрическими параметрами сечения. Вычисляются они как отношения моментов инерции к расстояниям от главных осей до наиболее удаленных от них точек сечения. Чтобы найти опасные точки, проведём по две пары касательных, параллельных главным осям U, V (по разные стороны от осей), и выберем те точки касания, которые наиболее удалены от главных осей (устанавливаем визуально или с помощью линейки). В рассматриваемом примере от оси V наиболее удалена т. А, а от оси U – т. В (рис. 1.5). Вычисляем главные координаты опасных точек, используя формулы аналитической геометрии:
где xA, yA, xB, yB, xC, yC – координаты точек А, В и центра тяжести C во вспомогательной системе координат XOY. Из рис. 1.5 находим
В п. 1.3.2 мы вычислили хC = 8,86 см; уC = 19,33 см. Подставляя в формулы эти значения, получаем
Знаки “минус” показывают, что точки удалены от главных осей в сторону отрицательного направления осей U и V. Определяем осевые моменты сопротивления
Пример расчёта и методические указания Подготовка исходных данных и расчётной схемы Решение задачи начинаем с выбора исходных данных из табл. 2.1 и 2.2 согласно шифру. Рассмотрим следующие параметры: Координаты узлов, мм: xА = 1568; yА = 15806; xВ = 4989; yВ = 17050; xС = 18409; yС = 21935; xD = 8409; yD = 7654. Коэффициенты: v 1 = 2; v 2 = 3; v 3 = 1. Силовое воздействие: F = 400 кН; βF =20о. Монтажное воздействие: δ 1 = –2 мм. Температурное воздействие: ∆t 3 = –20оС. Откладываем в масштабе М 1:100 координаты x, y узлов А, В, С, D в произвольно выбранной системе координат ХОУ и соединяем узел D с узлами А, В и С, в результате чего получаем трёхстержневую четырёхшарнирную конструкцию (рис. 2.2). К общему узлу D прикладываем внешнюю силу F под углом βF к горизонтальной оси Х. Показываем в масштабе М 10:1 неточность изготовления одного из стержней с учётом знака δ. При положительном δ стержень изображаем длиннее проектного, а при отрицательном δ – короче. Для рассматриваемого примера расчётная схема показана на рис. 2.3. Прочностная сторона задачи Здесь используем условия прочности стержней в виде двойных неравенств (2.6) и их решение по формулам (2.7):
i = 1: N 1 = R 2 = 446333 + 46,0431 A; с 1 = + 446333 H; di = 46,0431 МПа; v 1 = 2; Находим требуемый параметр площади
i = 2: N 2 = R 2= – 54650 – 54,2939 A; c 2 = – 54650 H; d 2 = –54,2939 МПа; v 2 =3; Находим требуемый параметр площади
i = 3: N 3 = – R 3 = –187680 + 19,2267 A; c 3 = – 187680 H; d 3 = 19,2267 МПа; v 3 = 1; Находим требуемый параметр площади
Из трёх значений параметра площади в качестве окончательного принимаем наибольшее как удовлетворяющее всем условиям прочности:
Вычисляем требуемые площади всех стержней Аi: А 1 = v 1 A = 2∙1629 = 3258 мм2; А 2 = v 2 А = 3 А = 3∙1629 = 4887 мм2; А 3 = v 3 А = А = 1629 мм2. ПЛОСКИЙ ИЗГИБ БАЛОК Плоский изгиб балок является одним из наиболее опасных случаев нагружения деталей машин и элементов сооружений, когда силовая плоскость проходит через одну из главных центральных осей инерции сечения (см. гл. 1). При плоском поперечном изгибе (в дальнейшем просто “изгибе”) в сечении балки возникают два внутренних усилия: поперечная сила Поперечная сила в произвольном сечении балки равна алгебраической сумме проекций на вертикальную ось Y всех внешних нагрузок, расположенных по одну сторону от рассматриваемого сечения, т. е.
При вычислениях используют следующее правило знаков (рис. 3.1):
Рис. 3.1. Правило знаков для поперечной силы внешняя нагрузка, вращающая отсечённый элемент балки (шарнирно закреплённый в центре тяжести сечения Изгибающий момент в произвольном сечении балки равен алгебраической сумме моментов относительно горизонтальной оси X всех внешних нагрузок, расположенных по одну сторону от рассматриваемого сечения, т. е.
При вычислениях используют следующее правило знаков (рис. 3.2):
Рис. 3.2. Правило знаков для изгибающего момента внешняя нагрузка, искривляющая отсечённый элемент балки (жёстко защемленный в рассматриваемом сечении i–i) выпуклостью вниз, создаёт положительный изгибающий момент, а выпуклостью вверх –отрицательный. С целью определения наиболее опасных сечений строят эпюры поперечных сил и изгибающих моментов по длине балки. Для проверки правильности построения эпюр используют третий закон Ньютона (действие равно противодействию) и дифференциальные зависимости между внутренними усилиями Q, M и интенсивностью распределённой нагрузки q. Ньютоновские проверки выполняют для каждой границы между грузовыми участками, где наблюдается изменение характера нагружения, например приложены сила или момент, начинается или заканчивается распределённая нагрузка и др. Эти проверки заключаются в выполнении условий
где Дифференциальные проверки должны выполняться для всех сечений балки. Обычно они записываются в виде
где d – дифференциал; z – абсцисса сечения (аргумент); Полезно помнить, что геометрический смысл первой производной – это тангенс угла наклона касательной к графику функции, а второй производной – кривизна функции в рассматриваемой точке. Угол наклона положителен, если он образован поворотом оси Z против часовой стрелки; кривизна положительна, если имеет выпуклость внизу; распределённая нагрузка положительна, если направлена вверх. Третий вид проверок – это интегральные зависимости между функциями
Здесь Полезно помнить, что приращение функции – это число, а интегралы в правой части – это площади, ограниченные графиком функции и осью Z в пределах грузового участка. При изгибе балки в точках её поперечных сечений появляются два вида напряжений: нормальные
где “–” в правой части объясняется тем, что при положительных значениях М и y появляются сжимающие напряжения Касательные напряжения имеют второстепенное значение при расчётах балок на прочность, так как сравнительно редко являются причиной разрушения. Эти напряжения зависят от поперечной силы и определяются по формуле Д.И. Журавского:
где С учётом вышесказанного расчёт балок выполняют, исходя из условия прочности по нормальным напряжениям
где При проектировочном расчёте балок на прочность, когда известны внешние нагрузки, типы опор, длина и материал балки, строят эпюру изгибающих моментов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 ,
, – функция прочности;
– функция прочности;  – обобщённый параметр внешних нагрузок;
– обобщённый параметр внешних нагрузок;  – обобщённый параметр формы и размеров стержня;
– обобщённый параметр формы и размеров стержня;  – обобщённый параметр упругих и механических характеристик материала.
– обобщённый параметр упругих и механических характеристик материала. при расчётах распадается на два независимых подпараметра
при расчётах распадается на два независимых подпараметра ,
, – параметр длины стержня;
– параметр длины стержня;  – параметр формы и размеров поперечного сечения стержня.
– параметр формы и размеров поперечного сечения стержня. ;
;  – статические моменты площади;
– статические моменты площади; ;
;  – осевые моменты инерции;
– осевые моменты инерции; – центробежный момент инерции;
– центробежный момент инерции; – полярный момент инерции,
– полярный момент инерции,


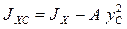 ;
;  ;
;  .
. между центральной осью XС и главной осью U (осью YС и осью V), (рис. 1.1),
между центральной осью XС и главной осью U (осью YС и осью V), (рис. 1.1),
 ;
; ; (1.2)
; (1.2) .
.
 (1.3)
(1.3) ;
;  ;
;  , (1.4)
, (1.4) ,
,  – координаты центра тяжести i -й простой фигуры в любой вспомогательной системе координат; Ai – площадь i -й простой фигуры; JXCi, JYCi, JXYCi – моменты инерции i -й простой фигуры относительно собственных центральных осей, параллельных осям вспомогательной системы;
– координаты центра тяжести i -й простой фигуры в любой вспомогательной системе координат; Ai – площадь i -й простой фигуры; JXCi, JYCi, JXYCi – моменты инерции i -й простой фигуры относительно собственных центральных осей, параллельных осям вспомогательной системы;  ;
;  – координаты центра тяжести i -й простой фигуры относительно центральных осей XC, YC всего поперечного сечения. Отметим, что в качестве “простой” фигуры может рассматриваться любая фигура, если у неё известно положение центра тяжести, площадь и значения моментов инерции.
– координаты центра тяжести i -й простой фигуры относительно центральных осей XC, YC всего поперечного сечения. Отметим, что в качестве “простой” фигуры может рассматриваться любая фигура, если у неё известно положение центра тяжести, площадь и значения моментов инерции. сумма осевых моментов инерции не изменяется, т.е. JX + JY = const – условие стационарности (инвариантности).
сумма осевых моментов инерции не изменяется, т.е. JX + JY = const – условие стационарности (инвариантности).








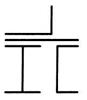


























 где
где 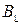 – больший размер уголка №10/6,3;
– больший размер уголка №10/6,3;  – высота швеллера № 10.
– высота швеллера № 10.
 ;
;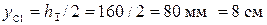 ;
; мм = 3,23 см;
мм = 3,23 см; мм = 17,42 см;
мм = 17,42 см; ;
; ;
; þ
þ  ;
; þ – z 0,þ
þ – z 0,þ 



 b = 200 мм;
h = 20 мм;
А = bh = 20 ∙ 2 = 40 см2;
JX = bh 3/12 = 20 ∙ 23/12 = 13,3 см4;
JY = b 3 h /12 = 203 ∙ 2/12 = 1333см4;
JXY = 0.
b = 200 мм;
h = 20 мм;
А = bh = 20 ∙ 2 = 40 см2;
JX = bh 3/12 = 20 ∙ 23/12 = 13,3 см4;
JY = b 3 h /12 = 203 ∙ 2/12 = 1333см4;
JXY = 0.

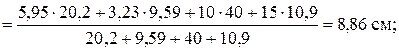



 ;
;  (i = 1 – 4):
(i = 1 – 4): ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
;  .
.
 ; относительная погрешность вычислений
; относительная погрешность вычислений  ⋍ 0,1 %.
⋍ 0,1 %.
 ; относительная погрешность вычислений
; относительная погрешность вычислений  ⋍ 0,2 %.
⋍ 0,2 %. .
. ;
;  ;
;  ;
; ;
; 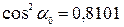 ;
;  .
. ;
;  – верно.
– верно.
 ;
;
 ;
;
 .
. ; JU + JV = 5624+1894 = 7518
; JU + JV = 5624+1894 = 7518  .
. . Относительная погрешность
. Относительная погрешность
 ;
; ,
, ;
;  ;
; ;
;  .
. см;
см; см.
см. ;
;  .
.
 МПа.
МПа.

 МПа.
МПа.
 МПа.
МПа.

 и изгибающий момент
и изгибающий момент  , расположенные в силовой плоскости YOZ.
, расположенные в силовой плоскости YOZ. . Поскольку все нагрузки
. Поскольку все нагрузки  параллельны оси Y и пары сил
параллельны оси Y и пары сил  не дают проекций на оси, определение поперечной силы можно упростить, полагая, что она равна алгебраической сумме нагрузок (кроме пар сил), расположенных по одну сторону от сечения, т. е.
не дают проекций на оси, определение поперечной силы можно упростить, полагая, что она равна алгебраической сумме нагрузок (кроме пар сил), расположенных по одну сторону от сечения, т. е. . (3.1)
. (3.1)
 ) по ходу часовой стрелки, создаёт положительную поперечную силу, а против часовой стрелки –отрицательную.
) по ходу часовой стрелки, создаёт положительную поперечную силу, а против часовой стрелки –отрицательную. . Учитывая расположение нагрузок, определение изгибающего момента можно упростить, полагая, что он равен алгебраической сумме моментов отсечённых нагрузок относительно центра тяжести сечения, т. е.
. Учитывая расположение нагрузок, определение изгибающего момента можно упростить, полагая, что он равен алгебраической сумме моментов отсечённых нагрузок относительно центра тяжести сечения, т. е. . (3.2)
. (3.2)
 ;
;  , (3.3)
, (3.3) – разрыв функции I рода (скачок);
– разрыв функции I рода (скачок);  и
и  – поперечная сила справа и слева от границы k;
– поперечная сила справа и слева от границы k;  и
и  – изгибающий момент справа и слева от границы k;
– изгибающий момент справа и слева от границы k;  – внешняя сосредоточенная сила на k -й границе;
– внешняя сосредоточенная сила на k -й границе;  – внешний сосредоточенный момент на k -й границе.
– внешний сосредоточенный момент на k -й границе.

 (3.4)
(3.4) ,
,  ,
,  – функции, характеризующие изменение по длине балки распределённой нагрузки, поперечной силы и изгибающего момента.
– функции, характеризующие изменение по длине балки распределённой нагрузки, поперечной силы и изгибающего момента.
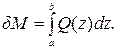 (3.5)
(3.5) – приращение функции; а, b – абсциссы начала и конца грузового участка.
– приращение функции; а, b – абсциссы начала и конца грузового участка. и касательные
и касательные  . Нормальные напряжения, играющие решающую роль при разрушении балок, создаются изгибающим моментом и определяются по формуле
. Нормальные напряжения, играющие решающую роль при разрушении балок, создаются изгибающим моментом и определяются по формуле
 – изгибающий момент в рассматриваемом сечении;
– изгибающий момент в рассматриваемом сечении;  – осевой момент инерции относительно главной центральной оси X; y –расстояние от оси X до точки, в которой определяется напряжение; знак
– осевой момент инерции относительно главной центральной оси X; y –расстояние от оси X до точки, в которой определяется напряжение; знак
 – поперечная сила в рассматриваемом сечении;
– поперечная сила в рассматриваемом сечении;  – статический момент площади сечения, расположенной по одну сторону от исследуемой точки;
– статический момент площади сечения, расположенной по одну сторону от исследуемой точки;  (3.6)
(3.6) – наибольший по модулю изгибающий момент, возникающий в балке;
– наибольший по модулю изгибающий момент, возникающий в балке;  – осевой момент сопротивления поперечного сечения;
– осевой момент сопротивления поперечного сечения;  – допускаемые напряжения при растяжении или сжатии.
– допускаемые напряжения при растяжении или сжатии.


