
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрение единичных состояний основной системыСодержание книги
Поиск на нашем сайте
Переобозначаем дополнительные реакции, соответствующие отброшенным связям
Проверяем выполнение уравнения (5.14):
Далее, по аналогии с грузовым состоянием составляем и исследуем выражения “единичных” изгибающих моментов (рис. 5.5, д). I грузовой участок
II грузовой участок
III грузовой участок
IV грузовой участок
V грузовой участок
По полученным данным строим со стороны сжатых волокон I “единичную” эпюру изгибающих моментов
Рис. 5.7. Статическая проверка эпюры Второе единичное состояние получаем, загружая основную систему единичной силой
Проверяем выполнение уравнения (5.14):
Составляем и исследуем выражения “единичных” изгибающих моментов по всем грузовым участкам (рис. 5.5, ж). I грузовой участок
II грузовой участок
III грузовой участок
IV грузовой участок
V грузовой участок
По полученным данным строим II “единичную” эпюру изгибающих моментов со стороны сжатых волокон (рис. 5.5, з). Проверяем равновесие узлов рамы:
Рис. 5.8. Статическая проверка эпюры
Вычисление коэффициентов канонических уравнений Метода сил Система уравнений (5.3) для случая
Податливости
Проверяем правильность вычисления коэффициентов. С этой целью строим суммарную “единичную” эпюру
Проверяем выполнение тождеств
Относительная погрешность
Решение системы канонических уравнений Подставляем найденные коэффициенты в уравнения (5.3) и решаем полученную систему относительно дополнительных неизвестных
Проверяем правильность решения путём обратной подстановки в систему
Вычисление опорных реакций для заданной схемы Используя принцип суперпозиции, находим по формуле (5.7):
Проверяем правильность реакций путём подстановки в уравнение (5.14):
Построение эпюры изгибающих моментов Для заданной схемы рамы Вначале строим исправленные эпюры моментов для основной системы путём преобразования “единичных” эпюр
т. е. все характерные ординаты эпюры Окончательную эпюру изгибающих моментов в заданной системе получаем, используя формулу (5.8):
Сложение по характерным точкам производим аналогично построению суммарной “единичной” эпюры
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.97 (0.01 с.) |

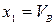 ;
; 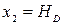 . Первое единичное состояние получаем, загружая основную систему единичной силой
. Первое единичное состояние получаем, загружая основную систему единичной силой 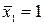 (рис. 5.5, д). Обозначаем основные реакции
(рис. 5.5, д). Обозначаем основные реакции 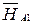 ,
, 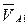 ,
, 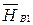 ,
, 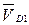 и для их определения обращаемся к уравнениям (5.10) – (5.13). Производим замену переменных и учитываем, что
и для их определения обращаемся к уравнениям (5.10) – (5.13). Производим замену переменных и учитываем, что 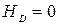 ,
, 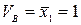 и все внешние нагрузки отсутствуют, т. е.
и все внешние нагрузки отсутствуют, т. е. 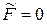 . В результате получаем систему уравнений и её решение
. В результате получаем систему уравнений и её решение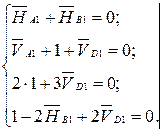
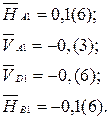
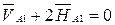 ;
; 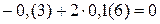 ;
; 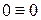 .
.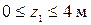
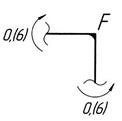
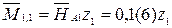 – наклонная прямая (0; 0,(6)) – сжатие волокон слева.
– наклонная прямая (0; 0,(6)) – сжатие волокон слева.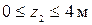
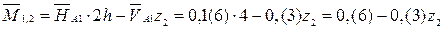 – наклонная прямая (0,(6); –0,(6)) – сжатие волокон сверху переходит в сжатие волокон снизу.
– наклонная прямая (0,(6); –0,(6)) – сжатие волокон сверху переходит в сжатие волокон снизу.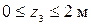
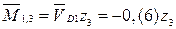 – наклонная прямая (0; –1,(3)) – истинное сжатие волокон снизу (реакция
– наклонная прямая (0; –1,(3)) – истинное сжатие волокон снизу (реакция 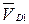 отрицательна и, следовательно, действует вниз).
отрицательна и, следовательно, действует вниз).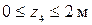
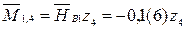 – наклонная прямая (0; – 0,(3)) – истинное сжатие волокон справа.
– наклонная прямая (0; – 0,(3)) – истинное сжатие волокон справа.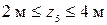
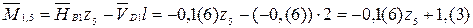 –наклонная прямая (1,0; 0,(6)) – сжатие волокон слева.
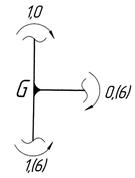
–наклонная прямая (1,0; 0,(6)) – сжатие волокон слева.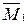 (рис. 5.5, е). Проверяем равновесие узлов рамы (рис. 5.7):
(рис. 5.5, е). Проверяем равновесие узлов рамы (рис. 5.7):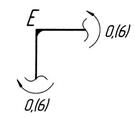
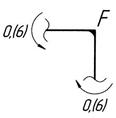
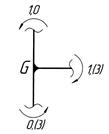
 ;
;
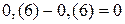 ;
;
 .
.
 ;
;
 ;
;
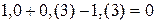 ;
;
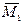
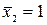 (рис. 5.5, ж). Используя уравнения (5.10) – (5.13) и учитывая, что
(рис. 5.5, ж). Используя уравнения (5.10) – (5.13) и учитывая, что 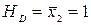 ;
; 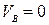 и
и 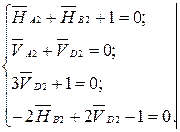
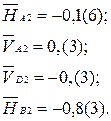
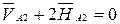 ;
; 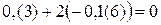 ;
; 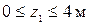
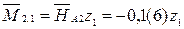 – наклонная прямая (0;– 0,(6)) – сжатие волокон справа.
– наклонная прямая (0;– 0,(6)) – сжатие волокон справа.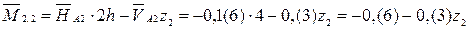 – наклонная прямая (–0,(6); 0,(6)) – сжатие волокон снизу переходит в сжатие волокон сверху.
– наклонная прямая (–0,(6); 0,(6)) – сжатие волокон снизу переходит в сжатие волокон сверху.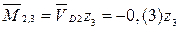 – наклонная прямая (0; –0,(6)) – истинное сжатие волокон снизу.
– наклонная прямая (0; –0,(6)) – истинное сжатие волокон снизу.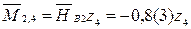 – наклонная прямая (0; – 1,(6)) – истинное сжатие волокон справа.
– наклонная прямая (0; – 1,(6)) – истинное сжатие волокон справа.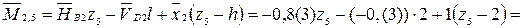
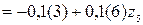 –наклонная прямая (–1; – 0,(6)) – сжатие волокон справа.
–наклонная прямая (–1; – 0,(6)) – сжатие волокон справа.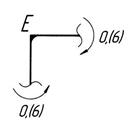
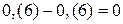 ;
;
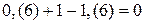 ;
;
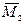
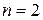 принимает вид
принимает вид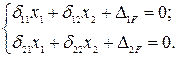
 и перемещения от нагрузки
и перемещения от нагрузки  находим по формулам (5.4) – (5.6). Так как изгибные жёсткости всех стержней рамы одинаковы, принимаем для простоты
находим по формулам (5.4) – (5.6). Так как изгибные жёсткости всех стержней рамы одинаковы, принимаем для простоты 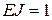 :
: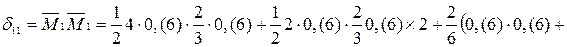
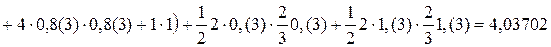 ;
;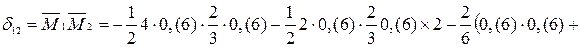
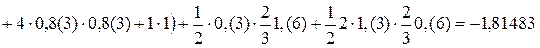 ;
;
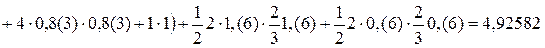 ;
;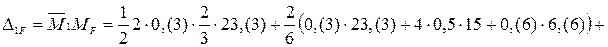
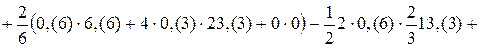
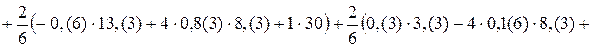
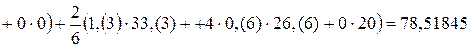 ;
; 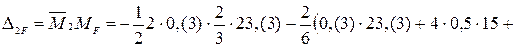
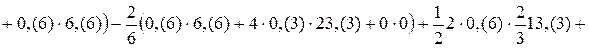
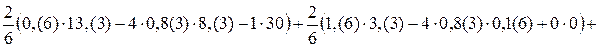
 .
. , складывая алгебраически значения моментов в характерных точках (если ординаты
, складывая алгебраически значения моментов в характерных точках (если ординаты 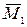 и
и 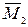 по одну сторону от оси, то складываем их, а если по разные стороны, то вычитаем их и разность откладываем со стороны большей ординаты) (рис. 5.5, л). Умножаем полученную эпюру саму на себя, а также на грузовую эпюру изгибающих моментов
по одну сторону от оси, то складываем их, а если по разные стороны, то вычитаем их и разность откладываем со стороны большей ординаты) (рис. 5.5, л). Умножаем полученную эпюру саму на себя, а также на грузовую эпюру изгибающих моментов  . Находим
. Находим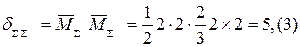 ;
;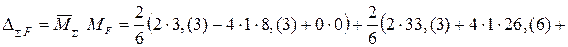
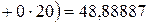 .
.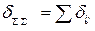 и
и 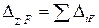 :
: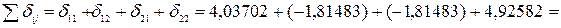
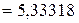 ≃
≃ 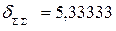 .
.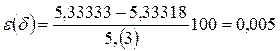 % – высокая точность вычислений.
% – высокая точность вычислений. ;
; 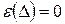 .
.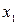 и
и 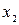 :
: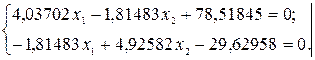
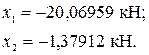
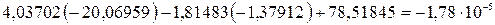 ≃0;
≃0;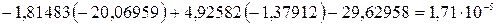 ≃0.
≃0.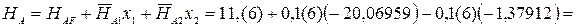
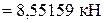 ;
;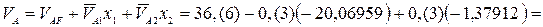
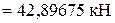 ;
;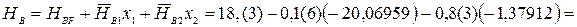
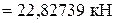 ;
;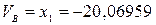
 ;
; 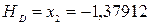
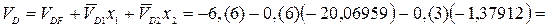
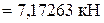 .
.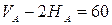 ;
; 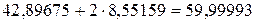 ≃60.
≃60.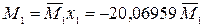 ;
; 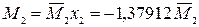 ,
,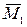 умножаем на значение
умножаем на значение 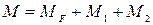 .
. . Результирующая эпюра
. Результирующая эпюра 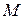 показана на рис. 5.5, л.
показана на рис. 5.5, л.


