
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка правильности решения задачиСодержание книги
Поиск на нашем сайте 1. Статическая проверка. Вычисляем окончательные значения опорных реакций и продольных сил R 1 = 446333 + 46,0431∙1629 = 521337 Н; R 2 = –54650 – 54,2939∙1629 = –143095 Н; R 3 = 187680 – 19,2267∙1629 = 156360 Н. N 1 = R 1 = 521337 Н; N 2 = R 2= – 143095 Н; N 3 = – R 3 = – 156360 Н. Согласно геометрическому условию равновесия для системы сходящихся сил (F, R 1, R 2, R 3) необходимо и достаточно, чтобы силовой многоугольник получился замкнутым. Выбираем масштабный коэффициент из условия, чтобы активная сила F изображалась вектором длиной 100 мм
Тогда реактивные силы будут изображаться векторами, длины которых, соответственно, равны: для R 1: Силовой многоугольник начинаем строить из произвольно выбранного полюса О, проводя последовательно вектора
Рис. 2.5. Статическая проверка. Построение силового многоугольника Абсолютная ошибка ∆F пропорциональна отрезку 4–0. В примере он составляет 0,5 мм, что соответствует ∆F = (4–0)∙ Если ошибка превышает допустимую величину, то необходимо проверить построения, а затем исходные уравнения (2.8). 2. Кинематическая проверка. Она заключается в построении действительной (упрощённой) схемы перемещений т. D, принадлежащей одновременно всем трём стержням системы. После мысленного разъединения стержней, их деформирования на величину ∆li и поворота относительно шарниров А, В, С на некоторые малые углы γi концы стержней должны соединиться в одной точке (т. D 1). Вычисляем абсолютные деформации стержней:
Выбираем произвольно т. D и из неё проводим лучи по направлению трёх стержней, т.е. под углами β 1, β 2, β 3 к горизонтали (оси Х). От концов стержней (с учётом неточности изготовления) откладываем в масштабе М 10:1 (можно М 5:1) отрезки ∆ li с учетом их знаков и восстанавливаем перпендикуляры до их взаимного пересечения (рис. 2.6). Абсолютная ошибка ∆∆ l пропорциональна наибольшей стороне треугольника невязки
Если ошибка превышает допустимую величину, то необходимо проверить построения (рис. 2.6), а затем преобразования уравнения (2.10) в уравнение (2.11).
Рис. 2.6. Кинематическая проверка. Построение схемы перемещений 3. Физическая проверка. Обозначим через При неправильном решении задачи угол получится в пределах 4. Прочностная проверка. Вычисляем действительные напряжения в стержнях σ i и сравниваем их с допускаемыми
Мы видим, что условия прочности выполняются, при этом одно из действительных напряжений Так как в рассматриваемом примере все проверки выполняются, то с большой вероятностью можно считать, что задача решена правильно и окончательно можно принять следующие площади стержней: А 1 = 3258 мм2; А 2 = 4887 мм2; А 3 = 1629 мм2.
ПЛОСКИЙ ИЗГИБ БАЛОК Плоский изгиб балок является одним из наиболее опасных случаев нагружения деталей машин и элементов сооружений, когда силовая плоскость проходит через одну из главных центральных осей инерции сечения (см. гл. 1). При плоском поперечном изгибе (в дальнейшем просто “изгибе”) в сечении балки возникают два внутренних усилия: поперечная сила Поперечная сила в произвольном сечении балки равна алгебраической сумме проекций на вертикальную ось Y всех внешних нагрузок, расположенных по одну сторону от рассматриваемого сечения, т. е.
При вычислениях используют следующее правило знаков (рис. 3.1):
Рис. 3.1. Правило знаков для поперечной силы внешняя нагрузка, вращающая отсечённый элемент балки (шарнирно закреплённый в центре тяжести сечения Изгибающий момент в произвольном сечении балки равен алгебраической сумме моментов относительно горизонтальной оси X всех внешних нагрузок, расположенных по одну сторону от рассматриваемого сечения, т. е.
При вычислениях используют следующее правило знаков (рис. 3.2):
Рис. 3.2. Правило знаков для изгибающего момента внешняя нагрузка, искривляющая отсечённый элемент балки (жёстко защемленный в рассматриваемом сечении i–i) выпуклостью вниз, создаёт положительный изгибающий момент, а выпуклостью вверх –отрицательный. С целью определения наиболее опасных сечений строят эпюры поперечных сил и изгибающих моментов по длине балки. Для проверки правильности построения эпюр используют третий закон Ньютона (действие равно противодействию) и дифференциальные зависимости между внутренними усилиями Q, M и интенсивностью распределённой нагрузки q. Ньютоновские проверки выполняют для каждой границы между грузовыми участками, где наблюдается изменение характера нагружения, например приложены сила или момент, начинается или заканчивается распределённая нагрузка и др. Эти проверки заключаются в выполнении условий
где Дифференциальные проверки должны выполняться для всех сечений балки. Обычно они записываются в виде
где d – дифференциал; z – абсцисса сечения (аргумент); Полезно помнить, что геометрический смысл первой производной – это тангенс угла наклона касательной к графику функции, а второй производной – кривизна функции в рассматриваемой точке. Угол наклона положителен, если он образован поворотом оси Z против часовой стрелки; кривизна положительна, если имеет выпуклость внизу; распределённая нагрузка положительна, если направлена вверх. Третий вид проверок – это интегральные зависимости между функциями
Здесь Полезно помнить, что приращение функции – это число, а интегралы в правой части – это площади, ограниченные графиком функции и осью Z в пределах грузового участка. При изгибе балки в точках её поперечных сечений появляются два вида напряжений: нормальные
где “–” в правой части объясняется тем, что при положительных значениях М и y появляются сжимающие напряжения Касательные напряжения имеют второстепенное значение при расчётах балок на прочность, так как сравнительно редко являются причиной разрушения. Эти напряжения зависят от поперечной силы и определяются по формуле Д.И. Журавского:
где С учётом вышесказанного расчёт балок выполняют, исходя из условия прочности по нормальным напряжениям
где При проектировочном расчёте балок на прочность, когда известны внешние нагрузки, типы опор, длина и материал балки, строят эпюру изгибающих моментов
3.1. Варианты и исходные данные домашнего задания № 3
На рис. 3.3, а изображена ось балки длиной
Рис. 3.3. Геометрическая ось балки, опоры и нагрузки
Таблица 3.1 Точки опирания и приложения нагрузок
а – первая цифра шифра; б – вторая цифра шифра.
Таблица 3.2 Числовые значения внешних нагрузок
Примечание. Знак “–” при числовых значениях нагрузок означает, что их направления необходимо показывать на схеме балки противоположно тем, которые изображены на рис. 3.1, б. В дальнейших расчётах значения нагрузок следует принимать по модулю, т. е. положительными. 3.2. Условие задания Для данной схемы балки необходимо: 1. Определить реакции для трёх случаев опирания: а) в шарнирно опёртой балке согласно исходной предпосылке; б) в консольной балке с жёстким защемлением (глухой заделкой) в т. А при отсутствии опоры в т. В; в) в шарнирно сочленённой балке с глухой заделкой в т. А, подвижной опорой в т. В и внутренним шарниром в т. С Î(А, В). 2. Построить эпюры поперечных сил и изгибающих моментов для шарнирно опёртой балки. 3. Подобрать размеры поперечных сечений различной формы из условия прочности по нормальным напряжениям при 4. Провести анализ экономичности принятых видов сечений. Пример расчёта и методические указания Подготовка исходных данных и расчётной схемы балки Решение задачи начинаем с выбора исходных данных из табл. 3.1 и 3.2. В качестве примера рассмотрим следующие данные. Длина балки Точки опирания и приложения нагрузок: NA = 3; NB = 10;
Числовые значения внешних нагрузок: М = 40
Используя исходные данные, изображаем расчётную схему. Длину балки чертим в масштабе М 1: 50 (в 2 см схемы – 1 мдлины балки). Так как табличные значения
Рис. 3.4. Расчетная схема шарнирно опёртой балки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


 ≃130 мм; для R 2:
≃130 мм; для R 2:  ≃36 мм; для R 3:
≃36 мм; для R 3: 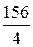 ≃39 мм.
≃39 мм. под углами к оси Х (горизонтали) соответственно равными βF, β 1, β 2, β 3 (рис. 2.5). При положительных значениях реакций Ri направления векторов
под углами к оси Х (горизонтали) соответственно равными βF, β 1, β 2, β 3 (рис. 2.5). При положительных значениях реакций Ri направления векторов  на рис. 2.3 и 2.5 должны совпадать, а при отрицательных значениях реакций эти векторы должны быть противоположны.
на рис. 2.3 и 2.5 должны совпадать, а при отрицательных значениях реакций эти векторы должны быть противоположны.
 = 0,5∙4 = 2 кН. Относительная погрешность по сравнению с активной силой
= 0,5∙4 = 2 кН. Относительная погрешность по сравнению с активной силой 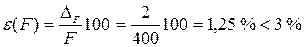 – допустимая величина.
– допустимая величина. мм – удлинение;
мм – удлинение;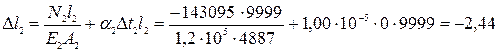 мм – укорочение;
мм – укорочение; мм – укорочение.
мм – укорочение. В рассматриваемом примере ∆∆ l =
В рассматриваемом примере ∆∆ l =  = = 2,5 мм. Относительную погрешность находим по сравнению с наибольшим значением деформации с учётом масштаба по рис. 2.6 (∆ l) max = |∆ l 3|= =112 мм
= = 2,5 мм. Относительную погрешность находим по сравнению с наибольшим значением деформации с учётом масштаба по рис. 2.6 (∆ l) max = |∆ l 3|= =112 мм ≃
≃  – допустимая величина.
– допустимая величина.
 угол, образованный вектором полного действительного перемещения узла
угол, образованный вектором полного действительного перемещения узла  и вектором сосредоточенной силы
и вектором сосредоточенной силы  . Так как в процессе деформирования системы сила F играет активную роль, а перемещение f – пассивную роль, то угол φ должен находиться в пределах
. Так как в процессе деформирования системы сила F играет активную роль, а перемещение f – пассивную роль, то угол φ должен находиться в пределах  . В рассматриваемом примере это условие выполняется: φ ≃ 450.
. В рассматриваемом примере это условие выполняется: φ ≃ 450. . В этом случае необходимо проверить построения (рис. 2.6), а также физическую сторону задачи (п. 2.3.5) и синтез (п. 2.3.6).
. В этом случае необходимо проверить построения (рис. 2.6), а также физическую сторону задачи (п. 2.3.5) и синтез (п. 2.3.6). или
или  :
:
 МПа ≃
МПа ≃  ;
; МПа >
МПа >  ;
; МПа >
МПа >  .
. получилось равным допускаемому, а остальные по модулю меньше допускаемых. Если условия не выполняются, то необходимо проверить подбор параметра площади А и вычисление площадей сечений Аi (п. 2.3.7).
получилось равным допускаемому, а остальные по модулю меньше допускаемых. Если условия не выполняются, то необходимо проверить подбор параметра площади А и вычисление площадей сечений Аi (п. 2.3.7). и изгибающий момент
и изгибающий момент  , расположенные в силовой плоскости YOZ.
, расположенные в силовой плоскости YOZ. . Поскольку все нагрузки
. Поскольку все нагрузки  параллельны оси Y и пары сил
параллельны оси Y и пары сил  не дают проекций на оси, определение поперечной силы можно упростить, полагая, что она равна алгебраической сумме нагрузок (кроме пар сил), расположенных по одну сторону от сечения, т. е.
не дают проекций на оси, определение поперечной силы можно упростить, полагая, что она равна алгебраической сумме нагрузок (кроме пар сил), расположенных по одну сторону от сечения, т. е. . (3.1)
. (3.1)
 ) по ходу часовой стрелки, создаёт положительную поперечную силу, а против часовой стрелки –отрицательную.
) по ходу часовой стрелки, создаёт положительную поперечную силу, а против часовой стрелки –отрицательную. . Учитывая расположение нагрузок, определение изгибающего момента можно упростить, полагая, что он равен алгебраической сумме моментов отсечённых нагрузок относительно центра тяжести сечения, т. е.
. Учитывая расположение нагрузок, определение изгибающего момента можно упростить, полагая, что он равен алгебраической сумме моментов отсечённых нагрузок относительно центра тяжести сечения, т. е. . (3.2)
. (3.2)
 ;
;  , (3.3)
, (3.3) – разрыв функции I рода (скачок);
– разрыв функции I рода (скачок);  и
и  – поперечная сила справа и слева от границы k;
– поперечная сила справа и слева от границы k;  и
и  – изгибающий момент справа и слева от границы k;
– изгибающий момент справа и слева от границы k;  – внешняя сосредоточенная сила на k -й границе;
– внешняя сосредоточенная сила на k -й границе;  – внешний сосредоточенный момент на k -й границе.
– внешний сосредоточенный момент на k -й границе.

 (3.4)
(3.4) ,
,  ,
,  – функции, характеризующие изменение по длине балки распределённой нагрузки, поперечной силы и изгибающего момента.
– функции, характеризующие изменение по длине балки распределённой нагрузки, поперечной силы и изгибающего момента.
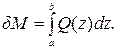 (3.5)
(3.5) – приращение функции; а, b – абсциссы начала и конца грузового участка.
– приращение функции; а, b – абсциссы начала и конца грузового участка. и касательные
и касательные  . Нормальные напряжения, играющие решающую роль при разрушении балок, создаются изгибающим моментом и определяются по формуле
. Нормальные напряжения, играющие решающую роль при разрушении балок, создаются изгибающим моментом и определяются по формуле
 – изгибающий момент в рассматриваемом сечении;
– изгибающий момент в рассматриваемом сечении;  – осевой момент инерции относительно главной центральной оси X; y –расстояние от оси X до точки, в которой определяется напряжение; знак
– осевой момент инерции относительно главной центральной оси X; y –расстояние от оси X до точки, в которой определяется напряжение; знак
 – поперечная сила в рассматриваемом сечении;
– поперечная сила в рассматриваемом сечении;  – статический момент площади сечения, расположенной по одну сторону от исследуемой точки;
– статический момент площади сечения, расположенной по одну сторону от исследуемой точки;  (3.6)
(3.6) – наибольший по модулю изгибающий момент, возникающий в балке;
– наибольший по модулю изгибающий момент, возникающий в балке;  – осевой момент сопротивления поперечного сечения;
– осевой момент сопротивления поперечного сечения;  – допускаемые напряжения при растяжении или сжатии.
– допускаемые напряжения при растяжении или сжатии. и задаются формой поперечного сечения
и задаются формой поперечного сечения  . По эпюре
. По эпюре  , а по форме сечения выражают
, а по форме сечения выражают  через характерный размер сечения а. Используя условие прочности, находят параметр а, решив соответствующее кубическое уравнение
через характерный размер сечения а. Используя условие прочности, находят параметр а, решив соответствующее кубическое уравнение
 , которая разделена на девять равных частей узловыми точками 0, 1, …, 9, а на 3.3, б показаны опоры, внешние нагрузки и номера точек их приложения. Вариант задания, т. е. схему опирания и нагружения балки, определяют по табл. 3.1 согласно шифру – двум последним цифрам зачётной книжки студента. Числовые данные нагрузок принимают по табл. 3.2 согласно второй цифре шифра.
, которая разделена на девять равных частей узловыми точками 0, 1, …, 9, а на 3.3, б показаны опоры, внешние нагрузки и номера точек их приложения. Вариант задания, т. е. схему опирания и нагружения балки, определяют по табл. 3.1 согласно шифру – двум последним цифрам зачётной книжки студента. Числовые данные нагрузок принимают по табл. 3.2 согласно второй цифре шифра.







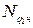



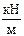

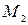





 .
. .
. = 3;
= 3; = 8;
= 8;  = 10.
= 10. ;
;  = –20 кН/м.
= –20 кН/м.



