
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт балок методом начальных параметровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод начальных параметров (МНП) является одним из основных при исследовании напряжённо-деформированного состояния стержневых конструкций, работающих преимущественно на изгиб. Весьма удачным приложением этого метода можно считать его использование при расчёте на прочность и жёсткость статически неопределимых балок, несущих различные виды внешних нагрузок. Метод начальных параметров настолько формализован, что позволяет легко вычислять внутренние усилия и перемещения в любом сечении балки путём подстановки значений нагрузок в канонические выражения, вид которых не зависит от числа грузовых участков. Согласно МНП для балок, нагруженных парами сил, сосредоточенными силами и распределёнными нагрузками, изменяющимися по линейному закону, выражения для поперечной силы
где Разрывы функции I и II рода для распределённой нагрузки на k -й границе определяются по формулам
где В МНП начало координат (0-я граница) всегда располагается на левом конце балки, а положительными нагрузками считаются следующие: пары сил – по часовой стрелке; силы и распределённые нагрузки – направленные вверх (рис. 4.1).
Рис. 4.1. Положительные направления нагрузок в МНП Независимо от способа опирания балки из четырёх начальных параметров При расчёте статически неопределимых балок особых трудностей не возникает, так как для каждой “лишней” связи можно составить дополнительное уравнение, выражающее отсутствие перемещения по направлению наложенной связи. Раскрытие статической неопределимости сводится к совместному решению уравнений, получаемых на основе выражений (4.1) с учетом изложенных выше соображений.
4.1. Варианты и исходные данные домашнего задания № 4
На рис. 4.2, а изображена балка с четырьмя грузовыми участками, которая опирается на жёсткую заделку в т. 0и шарнирно-подвижную опору в т. 3. На рис. 4.2, б показаны типы внешних нагрузок и номера точек или участков их приложения. Вариант задания определяют по табл. 4.1 согласно шифру – двум последним цифрам зачётной книжки студента. Значения нагрузок и длин участков принимают из табл. 4.2 согласно второй цифре шифра.
Рис. 4.2. Схема опирания и нагружения балки
Таблица 4.1 Номера точек и участков приложения нагрузок
а – первая цифра шифра; б – вторая цифра шифра.
Таблица 4.2 Значения нагрузок и длин грузовых участков
Примечание. Знак “–” при числовых значениях нагрузок означает, что их направления необходимо показывать на схеме балки противоположно тем, которые изображены на рис. 4.1. б. В дальнейших расчётах значения нагрузок следует принимать по модулю, то есть положительными.
4.2. Условие задания Для заданной схемы балки необходимо: 1. Определить опорные реакции. 2. Построить эпюры поперечных сил, изгибающих моментов и прогибов. 3. Подобрать сечение балки в виде стального прокатного двутавра из условий прочности и жесткости, если 4. Произвести полную проверку правильности решения задачи.
Пример расчёта и методические указания Подготовка исходных данных и расчётной схемы балки Решение начинаем с выбора исходных данных из табл. 4.1 и 4.2. В качестве примера рассмотрим следующие данные. Номера точек и участков приложения нагрузок: Изображаем расчётную схему балки. Длину балки чертим в масштабе М 1:100 (в 1 см схемы – 1 м длины балки). Нагрузки
Определение опорных реакций Показываем реакции, возникающие в заделке n = R – U = 3 – 2 = 1. Для раскрытия неопределимости используем формулы метода начальных параметров для поперечной силы, изгибающего момента и прогиба (4.1). Учитывая специфику МНП (нумерация границ и правило знаков), выполним переприсвоение интенсивностей распределённых нагрузок, переходя от заданных обозначений к обозначениям МНП на основе расчётной схемы (рис. 4.3, а)
Рис. 4.3. Расчётная схема балки. Эпюры Q, M, Записываем и вычисляем все начальные и граничные параметры для k = 0, 1, 2, 3, используя расчётную схему (рис. 4.3, а) и формулы (4.2). k = 0: k = 1: k = 2: k = 3: k = 4: Подставляем начальные и граничные параметры в формулы (4.1) и разворачиваем суммы по всем грузовым участкам. В результате получаем выражения поперечной силы, изгибающего момента и прогиба для рассматриваемого варианта балки:
Заметим, что действие формул для i -го грузового участка распространяется от знака равенства до вертикальной черты с индексом i Г.У. В полученных функциональных зависимостях остаются неизвестными опорные реакции
где Для рассматриваемого варианта имеем при при Подставляя эти значения в выражения функций
на Объединяем уравнения (4.3) – (4.5) в систему и решаем её
Проверяем правильность решения системы путём обратной подстановки в уравнения
Выполняем статическую проверку правильности определения реакций, записав два уравнения равновесия балки (рис. 4.3, а):
Обратим внимание, что в данном примере трапецеидальная нагрузка
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 998; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

 , изгибающего момента
, изгибающего момента 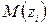 и прогиба
и прогиба  имеют следующий вид:
имеют следующий вид: ;
; ; (4.1)
; (4.1)
 ,
, – прогиб в начале балки;
– прогиб в начале балки;  – угол поворота в начале балки;
– угол поворота в начале балки; 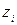 – абсцисса сечения, в котором определяются значения функций
– абсцисса сечения, в котором определяются значения функций 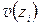 ;
;  – расстояние от начала балки до k -й границы;
– расстояние от начала балки до k -й границы;  – внешний момент на k -й границе;
– внешний момент на k -й границе;  – внешняя сила на k -й границе;
– внешняя сила на k -й границе;  – скачок распределённой нагрузки на k -й границе;
– скачок распределённой нагрузки на k -й границе;  – скачок тангенса угла наклона распределённой нагрузки на k -й границе; i – номер сечения (участка) балки; k – номер границы между грузовыми участками;
– скачок тангенса угла наклона распределённой нагрузки на k -й границе; i – номер сечения (участка) балки; k – номер границы между грузовыми участками;  – изгибная жёсткость.
– изгибная жёсткость. ;
;  ;
;  ;
; 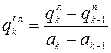 , (4.2)
, (4.2) и
и  – интенсивность нагрузки бесконечно близко справа и бесконечно близко слева от границы.
– интенсивность нагрузки бесконечно близко справа и бесконечно близко слева от границы.
 ,
,  ,
,  ,
,  два всегда известны, а два других параметра неизвестны. Для их вычисления используются конечные статические и (или) кинематические условия, зависящие от способа опирания балки. Например, в глухой заделке известны прогиб и угол поворота, но неизвестны поперечная сила и изгибающий момент; в шарнирной опоре известны прогиб и изгибающий момент, но неизвестны угол поворота и поперечная сила; на свободном крае балки известны поперечная сила и изгибающий момент, но неизвестны прогиб и угол поворота.
два всегда известны, а два других параметра неизвестны. Для их вычисления используются конечные статические и (или) кинематические условия, зависящие от способа опирания балки. Например, в глухой заделке известны прогиб и угол поворота, но неизвестны поперечная сила и изгибающий момент; в шарнирной опоре известны прогиб и изгибающий момент, но неизвестны угол поворота и поперечная сила; на свободном крае балки известны поперечная сила и изгибающий момент, но неизвестны прогиб и угол поворота.




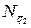

 ,
,

 ,
,

 ,
,

 ,
,
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
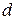 ,
,
 ,
,  .
. ;
;  ;
;  – отсутствует;
– отсутствует;  ;
; 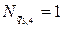 . Значение нагрузок и длин грузовых участков:
. Значение нагрузок и длин грузовых участков: 
 ;
; 
 ;
; 
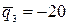



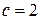

 ,
,  и шарнирно-подвижной опоре
и шарнирно-подвижной опоре  (рис. 4.3, а). Очевидно, что двух уравнений равновесия, которые можно записать для системы параллельных сил (
(рис. 4.3, а). Очевидно, что двух уравнений равновесия, которые можно записать для системы параллельных сил ( ;
;  ), недостаточно для вычисления трёх неизвестных (
), недостаточно для вычисления трёх неизвестных ( – слева от заделки (0-я граница) нагрузка отсутствует;
– слева от заделки (0-я граница) нагрузка отсутствует;

 ;
; 


 – справа от 4-й границы нагрузка отсутствует.
– справа от 4-й границы нагрузка отсутствует.
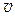
 – на опоре прогиб балки отсутствует;
– на опоре прогиб балки отсутствует;  – в глухой заделке угол поворота балки отсутствует;
– в глухой заделке угол поворота балки отсутствует;  – расстояние от левого края балки до 0-й границы;
– расстояние от левого края балки до 0-й границы;  – внешний момент равен неизвестному реактивному моменту в заделке;
– внешний момент равен неизвестному реактивному моменту в заделке;  – внешняя сила равна неизвестной опорной реакции в заделке;
– внешняя сила равна неизвестной опорной реакции в заделке; 
 – слева от заделки нагрузка отсутствует;
– слева от заделки нагрузка отсутствует; 
 – тангенс угла наклона трапецеидальной нагрузки;
– тангенс угла наклона трапецеидальной нагрузки; 

 ;
;  ;
; 

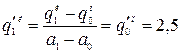


 ;
; 
 –нагрузка не изменяет своей интенсивности;
–нагрузка не изменяет своей интенсивности; 

 – нагрузка не изменяет своего наклона.
– нагрузка не изменяет своего наклона.
 ;
;  ;
;  –нагрузка не изменяет своей интенсивности;
–нагрузка не изменяет своей интенсивности; 

 – нагрузка не изменяет своего наклона.
– нагрузка не изменяет своего наклона.

 . Остальные параметры не рассматриваем, так как справа от 4-й границы участок балки отсутствует.
. Остальные параметры не рассматриваем, так как справа от 4-й границы участок балки отсутствует. ;
;
 ;
;
 .
. ,
, 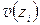 те их значения, которые заведомо известны без вычислений. Согласно методу сечений на конце балки поперечная сила равна приложенной там сосредоточенной силе, взятой с учётом знака, а изгибающий момент равен приложенной там паре сил, также взятой с учётом знака. Кроме того, учтём, что прогиб балки над жёсткой опорой всегда равен нулю. Таким образом, можно записать, что
те их значения, которые заведомо известны без вычислений. Согласно методу сечений на конце балки поперечная сила равна приложенной там сосредоточенной силе, взятой с учётом знака, а изгибающий момент равен приложенной там паре сил, также взятой с учётом знака. Кроме того, учтём, что прогиб балки над жёсткой опорой всегда равен нулю. Таким образом, можно записать, что ;
;  ;
;  ,
, – длина балки;
– длина балки;  – пролёт балки, равный расстоянию между опорами;
– пролёт балки, равный расстоянию между опорами;  – при вращении элемента балки по часовой стрелке;
– при вращении элемента балки по часовой стрелке;  – при изгибе элемента балки выпуклостью вниз.
– при изгибе элемента балки выпуклостью вниз.
 ;
; 
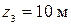
 .
. или
или ; (4.3)
; (4.3)
 или
или ; (4.4)
; (4.4)
 или, умножая
или, умножая ,
,  . (4.5)
. (4.5)



 – верно;
– верно; ≃726,660 – верно;
≃726,660 – верно; ≃120,147 – верно.
≃120,147 – верно.
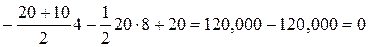 – выполняется;
– выполняется;

 – выполняется.
– выполняется. при вычислении моментов разбилась на прямоугольную с интенсивностью
при вычислении моментов разбилась на прямоугольную с интенсивностью  и треугольную с максимальной интенсивностью
и треугольную с максимальной интенсивностью  . В случае разнозначной трапеции, когда
. В случае разнозначной трапеции, когда  и
и  имеют противоположные знаки, трапеция разбивается на два треугольника, равнодействующие которых направлены в разные стороны. Учитывая, что согласно табл. 4.2 модули интенсивностей нагрузок
имеют противоположные знаки, трапеция разбивается на два треугольника, равнодействующие которых направлены в разные стороны. Учитывая, что согласно табл. 4.2 модули интенсивностей нагрузок  и
и  .
.


