
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статическая задача расчёта огнестойкости железобетонных конструкцийСодержание книги
Поиск на нашем сайте
Существенная неоднородность механических свойств и физическая нелинейность деформирования компонентов сечения железобетонного элемента, обусловленная его неравномерным нагревом, приводит к сложному характеру распределения напряжений по сечению, которое в большинстве случаев не удаётся прогнозировать заранее. Поэтому широко применяемые при нормальных температурных условиях аналитические методы расчёта по предельным усилиям, основанные на предварительном задании вида эпюры напряжений и последующим определением несущей способности из уравнений равновесия, в условиях неравномерного нагрева оказываются пригодными для решения лишь нескольких частных задач. Более широкими возможностями обладают численные методы, основанные на дискретизации расчётной схемы и непосредственном учёте физической нелинейности деформирования. Расчётную оценку огнестойкости стержневых железобетонных конструкций по прогибам или несущей способности нормального сечения достаточно удобно осуществлять на основе деформационной модели нормальных сечений железобетонных элементов [25]. Для расчёта по деформационной модели стержневая железобетонная конструкция представляется в дискретной форме – в виде набора элементов. По длине конструкция разделяется условными плоскостями, нормальными к продольной оси, на характерные объёмы – элементы стержня (далее – просто элементы). Длина элементов назначается так, чтобы принять в её пределах постоянными факторы силового и температурного воздействия, то есть внутренние усилия М, N и условия обогрева наружной поверхности конструкции. Поперечное сечение каждого элемента конструкции представляется в виде набора элементарных участков (компонентов сечения), в пределах которых все характеристики – температура, напряжения, деформации – принимаются постоянными (по значению в центре тяжести элементарного участка). Количество и размеры элементарных участков определяется особенностями напряженно-деформированного состояния, схемой нагрева и градиентом температур. В местах более интенсивного изменения напряжений и температур возможно увеличение числа элементарных участков при уменьшении их площади. Координаты центров тяжести элементарных участков и эксцентриситеты приложения продольного усилия отсчитываются от моментных осей, положение которых по высоте и ширине сечения выбирается произвольно. Продольная ось элемента z проходит через точку пересечения выбранных моментных осей.
Расчётная деформационная модель состоит из трёх общих для механики деформируемого твёрдого тела групп условий, а математическая модель – соответственно из трёх групп определяющих соотношений, которые применительно к плоскому изгибу в условиях температурного воздействия приобретают следующий вид: статические соотношения (уравнения равновесия)
где N, M – продольная сила и изгибающий момент от внешней нагрузки; s b,ti, s s,tj – напряжения на элементарных участках бетона и арматуры; Ab,i, As,j – площади элементарных участков; yb,i, ys,j – координаты центров тяжести элементарных участков относительно выбранной моментной оси; геометрические соотношения (уравнения совместности деформаций в соответствии с гипотезой плоских сечений)
где e b,ti , e s,tj и физические соотношения (уравнения состояния) s b,ti = e b,ti Eb,ti n b,ti , (5.28) s s,tj = e s,tj Es n s,tj, (5.29) где Eb,ti n b,ti, Es n s,tj – секущие модули деформаций соответственно бетона и арматуры; n b,ti, n s,tj – коэффициенты секущих модулей (по Н.И. Карпенко), или коэффициенты упругости (по В.И. Мурашёву); Eb,ti, Es – начальные модули деформаций бетона (при данной температуре нагрева) и арматуры. Для диаграммы деформирования бетона:
kb , ti = – ln (n bu , ti); (5.31)
где kb , ti – параметр нелинейности диаграммы; he, ti – уровень деформаций бетона, равный отношению силовых деформаций e b , ti к их предельной величине при данной температуре e bu , ti ; n bu , ti – предельный коэффициент секущего модуля при данной температуре: e bu , ti = e bu ,0 / b b , ti , (5.33) n bu , ti = n bu ,0 × g b , ti , (5.34) n bu ,0 = s bu ,0/(Eb ×e bu ,0); (5.35) e bu ,0 и n bu ,0 – соответственно предельные деформации и предельный коэффициент секущего модуля бетона до нагрева; допускается принимать для тяжёлого бетона на гранитном заполнителе и для конструкционного керамзитобетона e bu ,0 = 0,20%, для тяжёлого бетона на известняковом заполнителе e bu ,0 = 0,25%; s bu ,0 и Eb – прочность и начальный модуль деформаций бетона до нагрева; g b , ti и b b , ti – коэффициенты снижения соответственно прочности и начального модуля деформаций бетона при нагреве:
где tb , i – температура нагрева бетона, °С; g, b, m, n –опытные параметры (табл. 5.7). Температурные деформации бетона:
где ea – предельное значение температурных деформаций, к которому они асимптотически приближаются; a, p – опытные параметры (см. табл. 5.7). Таблица 5.7 Характеристики изменения свойств бетона при нагреве [25]
В случае растяжения температурная зависимость прочности бетона принимается такой же, как и при сжатии, а исходные характеристики s bu ,0 и e bu ,0 заменяются на s btu ,0 и e btu ,0. Для диаграммы деформирования арматуры: в стадии линейно-упругой работы (e s , tj £ e se , tj) n s , tj = 1; в стадии нелинейной работы (e se , tj < e s , tj < e sy):
где nD s , tj – локальный коэффициент секущего модуля на нелинейном участке, определяется по аналогии с диаграммой деформирования бетона:
k D s , tj – параметр нелинейности деформирования; hDe, tj – уровень приращения деформаций арматуры по отношению к деформациям предела упругости e se , tj: k D s , tj = – ln (nD sy , tj ); (5.41)
e se , tj = s se , tj / Es; (5.43) nD su , tj – предельный локальный коэффициент секущего модуля на нелинейном участке диаграммы:
s se , tj и s sy , tj – соответственно предел упругости и предел текучести арматуры при данной температуре нагрева: s se , tj = s se ,0 × g se , tj ; (5.45) s sy , tj = s sy ,0 × g sy , tj , (5.46) s se ,0 и s sy ,0 – предел упругости и предел текучести арматуры до нагрева; g se , tj и g sy , tj – коэффициенты снижения предела упругости и предела текучести при нагреве:
где ts , j – температура нагрева арматуры, °С; w y, w e, c, d – опытные параметры. В стадии текучести (e s , tj ³ e sy) диаграмма имеет неограниченный горизонтальный участок и s s , tj = s sy , tj:
Температурные деформации арматуры определяются при помощи коэффициента температурного расширения a s,t:
Основные температурные параметры арматуры класса А400 (А-III) показаны в табл. 5.8. Таблица 5.8 Основные температурные параметры арматуры класса А400 (A-III) [25]
Характерные температурные зависимости прочностных и деформативных характеристик, а также диаграммы деформирования бетона и арматуры при различных температурах нагрева, полученные по представленным выражениям, показаны на рис. 5.7 – 5.10. Для повышения точности расчёта температурные зависимости механических характеристик применяемых материалов рекомендуется уточнять экспериментально.

Рис. 5.7. Температурные зависимости коэффициентов снижения прочности gb,t и начального модуля деформаций bb,t (а),температурные деформации (б) тяжёлого бетона на гранитном заполнителе
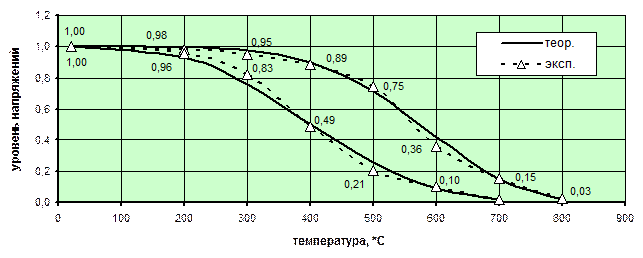 Рис. 5.9. Температурные зависимости параметров g sy , t и g se , t для арматуры класса А400 (А-III) Рис. 5.9. Температурные зависимости параметров g sy , t и g se , t для арматуры класса А400 (А-III)

Рис. 5.10. Диаграмма «напряжения – силовые деформации» арматуры класса А400 (А-III) при различных температурах нагрева При выводе физических соотношений (уравнений связи напряжений и деформаций) бетона и арматуры при нагреве приняты следующие исходные предпосылки и упрощающие гипотезы: нагрев осуществляется по стандартному температурному режиму, принятому для испытаний конструкций на огнестойкость; температурные зависимости механических свойств бетона и арматуры определяются по результатам нагрева до разрушения нагруженных образцов (при постоянных уровнях нагружения); деформирование бетона и арматуры условно принимается равновесным на всех стадиях работы (не зависящим от времени совместного воздействия температуры и нагрузки); силовые и температурные деформации материалов развиваются независимо друг от друга и к ним применим принцип аддитивности (сложения); предельные структурные напряжения в бетоне принимаются независящими от температуры нагрева (температурные зависимости для коэффициентов g b , ti и n bu , ti /n bu ,0 совпадают); температурная зависимость прочности бетона принята одинаковой при сжатии и растяжении; взрывообразного разрушения бетона при нагреве не происходит; максимальные деформации сжатия бетона и растяжения арматуры условно принимаются неограниченными, а при растяжении бетона ограничиваются точкой, соответствующей максимальным напряжениям; деформации e sy приняты не зависящими от температуры нагрева; температурные деформации арматуры развиваются линейно (коэффициент температурного расширения a s,t принят постоянным); модуль упругости арматуры принят не зависящим от температуры нагрева; восходящий участок на диаграмме деформирования арматуры, соответствующий её упрочнению после достижения предела текучести, не учитывается; при выводе математических соотношений для основных параметров, отражающих состояние материала при изменении температуры и нагрузки, использовано единое кинетическое уравнение нелинейного накопления повреждений при воздействии активного фактора
где у, а – соответственно текущее и предельное значения исследуемой характеристики; t – параметр активного воздействия (температура или деформации); k – параметр затухания процесса; m – показатель интенсивности. Решение этого уравнения при граничных условиях a = 0 и Принятые предпосылки дают возможность анализировать состояние элемента в любой момент времени нагрева независимо от его состояния в другие моменты времени. Решение нелинейной системы (5.24) – (5.29) осуществляется методом последовательных приближений, который может быть реализован как в форме метода переменных параметров упругости (последовательно уточняются коэффициенты секущего модуля), так и в форме непосредственного подбора значений e t и c t, соответствующим условиям равновесия. Результаты должны быть одинаковыми независимо от выбранной формы проведения расчёта. Метод переменных параметров упругости в большинстве случаев позволяет достаточно быстро решить конкретную задачу определения деформаций (c t, e t) при заданных усилиях (M, N). Однако для оценки несущей способности более удобным оказывается метод подбора, поскольку на этапах, непосредственно предшествующих исчерпанию несущей способности, итерационный процесс сходится очень медленно, а определять величину несущей способности по критерию полной потери сходимости итерационного процесса крайне нерационально. При использовании метода подбора предельный момент соответствует состоянию, когда кривизна начинает расти без увеличения нагрузки, то есть в сечении образуется пластический шарнир. Деформации бетона и арматуры при этом могут не достигать своих предельных значений. Параметры деформированного состояния (c t, e t), найденные в результате решения нелинейной системы (5.24) – (5.29), справедливы для сечения с трещиной, или для элемента стержня, у которого сцепление бетона и арматуры обеспечено лишь по торцам, а по длине отсутствует. В действительности усилия сцепления по длине элемента, сохраняющиеся в первые 40…60 мин нагрева, несколько уменьшают деформации растянутой арматуры и кривизну элемента. Этот эффект учитывается традиционным для теории железобетона коэффициентом В.И. Мурашёва y s , t, обеспечивающим переход от деформаций арматуры в сечении с трещиной к деформациям арматуры в составе железобетонного элемента (к так называемым средним деформациям). Далее по средним деформациям растянутой арматуры e s , t y s , t и крайнего сжатого волокна бетона e b , t 1 с применением гипотезы плоских сечений определяется кривизна элемента:
где s s,t и s s,crc – напряжения в растянутой арматуре соответственно действующие в рассматриваемый момент и действовавшие сразу после образования трещины; b t – коэффициент, учитывающий неразрывность функции деформаций элемента до и после трещинообразования, а также снижение сцепления арматуры с бетоном при нагреве:
e sm,crc и e s,crc – деформации арматуры непосредственно до и после образования трещины (резкое приращение деформаций в момент трещинообразования происходит в результате передачи усилия на арматуру с треснувшего бетона). Изгибная жёсткость элемента Dt:
где М и c t – текущее значение момента и соответствующая ему кривизна; c tem – температурная кривизна, возникающая вследствие неравномерного нагрева и определяемая при М = 0. Расчёт на огнестойкость проводится при нормативных сопротивлениях бетона и арматуры (s bu ,0 = Rbn; s btu ,0 = Rbt,n ; s sy ,0 = Rsn) на действие длительных нормативных нагрузок. При экспериментальных исследованиях для лучшей сходимости с опытными данными следует использовать средние характеристики. Оценка огнестойкости изгибаемых элементов. Наиболее удобным критерием наступления предела огнестойкости балочных конструкций, разрушение которых при пожаре может происходить как по арматуре, так и по бетону, является достижение максимальным прогибом конструкции f max, t предельно допустимой величины fult: f max, t ³ fult . (5.56) Как и в стандартной методике испытания балочных конструкций на огнестойкость (ГОСТ 30247.1-94 [9]), величина предельного прогиба fult может быть принята равной 1/20 пролёта. Максимальный прогиб при нагреве f max, t допустимо определять по кривизне наиболее нагруженного элемента c t, расположенного посередине пролёта:
где s – коэффициент, зависящий от схемы загружения; при равномерно распределённой нагрузке s = 5/48; l 0 – пролёт конструкции. При необходимости балочная конструкция может быть разделена по длине на некоторое количество элементов, а уточнённое значение её прогиба в произвольном сечении определёно по общим правилам строительной механики. Для сравнения результатов расчёт предела огнестойкости сплошных плит при одностороннем нагреве с достаточной точностью может был проведён с использованием метода критических температур А.И. Яковлева [23; 28]. Эпюра напряжений в сжатой зоне бетона принимается прямоугольной. При нагреве со стороны, где внешняя нагрузка вызывает растяжение (что характерно для пролётных сечений), снижение прочности бетона сжатой зоны не учитывается, а усилие в растянутой арматуре умножают на коэффициент g sy,t. Определяется критическое значение коэффициента снижения прочности арматуры при нагреве, представляющего собой уровень нагружения рабочей арматуры:
Из выражения (5.48) определяется критическая температура нагрева арматуры:
По кривой прогрева арматуры определяется момент времени, соответствующий её прогреву до критической температуры ts,cr. Найденный момент времени принимается в качестве предела огнестойкости конструкции по несущей способности R. Оценку огнестойкости балок и балочных плит, имеющих жёсткую заделку на опорах (такая схема моделирует работу плиты монолитного перекрытия) можно осуществлять с использованием метода предельного равновесия. Предел огнестойкости по несущей способности наступит, когда сумма предельных моментов в пролётном Мпр и опорном Моп сечениях снизится до величины усилия от действующей нагрузки в аналогичной свободно опёртой балке. В более общем случае (при несимметричных опорных закреплениях и т.п.) критерием исчерпания несущей способности является равенство суммы пролётного Мпр и полусуммы опорных (Моп,л и Моп,п) предельных моментов моменту от внешней нагрузки в аналогичной свободно опёртой балке. Например, при действии равномерно распределённой нагрузки q условие исчерпания несущей способности приобретает вид:
Примеры расчёта огнестойкости железобетонных конструкций методом критических температур можно найти в Пособии к СТО 36554501-006-2006. Оценка огнестойкости сжатых элементов. Оценка огнестойкости внецентренно сжатых колонн, работающих как со случайным, так и с расчётным эксцентриситетом, осуществляется на основе единого методологического подхода. В качестве расчётных усилий принимаются продольная сила N и изгибающий момент е = е 0×h, (5.61) где
Критическое усилие потери устойчивости колонны Ncr,t определяется по формуле Эйлера с использованием изгибной жёсткости Dt наиболее нагруженного элемента колонны, расположенного посередине её расчётной длины:
где l 0 – расчётная длина колонны. Как известно из сопротивления материалов, при значениях продольного усилия, близких к критическому (N ³ 0,75 Ncr), формула (13.62) даёт завышенные значения, поэтому в практических расчётах коэффициент h необходимо ограничивать и принимать h £ 4. Увеличение эксцентриситета приводит к возрастанию изгибающего момента и уменьшению изгибной жёсткости, поэтому расчёт ведётся методом последовательных приближений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.206 (0.009 с.) |

 , (5.24)
, (5.24) , (5.25)
, (5.25)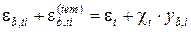 , (5.26)
, (5.26)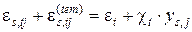 , (5.27)
, (5.27) ,
,  – соответственно силовые и температурные деформации бетона и арматуры; e t – обобщённая линейная деформация элемента, выражает удлинение (или укорочение) продольной оси; c t – обобщённая угловая деформация, выражает кривизну продольной оси (угол поворота торцевых сечений);
– соответственно силовые и температурные деформации бетона и арматуры; e t – обобщённая линейная деформация элемента, выражает удлинение (или укорочение) продольной оси; c t – обобщённая угловая деформация, выражает кривизну продольной оси (угол поворота торцевых сечений); ; (5.30)
; (5.30)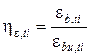 ; (5.32)
; (5.32) ; (5.36)
; (5.36) , (5.37)
, (5.37) , (5.38)
, (5.38)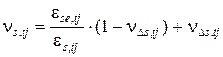 ; (5.39)
; (5.39)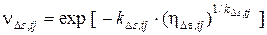 ; (5.40)
; (5.40) ; (5.42)
; (5.42) ; (5.44)
; (5.44) ; (5.47)
; (5.47)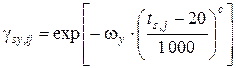 , (5.48)
, (5.48) . (5.49)
. (5.49) . (5.50)
. (5.50)
 Рис. 5.8. Диаграммы «напряжения – силовые деформации» тяжёлого бетона класса В20 на гранитном заполнителе при различных температурах нагрева
Рис. 5.8. Диаграммы «напряжения – силовые деформации» тяжёлого бетона класса В20 на гранитном заполнителе при различных температурах нагрева , (5.51)
, (5.51) имеет вид
имеет вид  , на основе которого построены выражения (5.30), (5.36), (5.37), (5.40), (5.47) и (5.48), а при a ¹ 0 и
, на основе которого построены выражения (5.30), (5.36), (5.37), (5.40), (5.47) и (5.48), а при a ¹ 0 и  – вид
– вид  , на основе которого построено выражение (5.38).
, на основе которого построено выражение (5.38). ; (5.52)
; (5.52) , (5.53)
, (5.53) . (5.54)
. (5.54)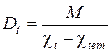 , (5.55)
, (5.55) , (5.57)
, (5.57) . (5.58)
. (5.58) . (5.59)
. (5.59) . (5.60)
. (5.60) , где е 0 – случайный или расчётный эксцентриситет. Увеличение эксцентриситета вследствие продольного изгиба колонны учитывается коэффициентом h:
, где е 0 – случайный или расчётный эксцентриситет. Увеличение эксцентриситета вследствие продольного изгиба колонны учитывается коэффициентом h: . (5.62)
. (5.62) , (5.63)
, (5.63)


