Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплотехническая задача расчёта огнестойкости железобетонных конструкцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Конструкции, оказавшиеся в среде с интенсивно повышающейся температурой, начинают прогреваться; возникающее температурное поле в общем случае является нестационарным и неоднородным, то есть изменяется во времени (t) и по координатам пространства (x, y, z). В большинстве случаев изменением температуры по длине конструкций и теплопотерями по их торцам допустимо пренебречь, и рассматривать только одномерные или двухмерные нестационарные температурные поля. Для плоских железобетонных элементов (плиты, стены) характерен односторонний нагрев и температура меняется в основном по толщине, поэтому рассматривается одномерное температурное поле. Для стержневых элементов характерными являются схемы нагрева с четырёх сторон (колонны) или с трёх сторон (балки, ригели), температура меняется по координатам сечения, поэтому рассматривается двухмерное температурное поле. Уравнение теплопроводности Фурье. Связь между температурой t, временем t и координатами элементарного объёма (x, y) выражается дифференциальным уравнением теплопроводности Фурье: для двухмерного температурного поля (вдоль осей x, y)
для одномерного температурного поля (вдоль оси x)
где t – температура, °C; t – время, с; r – плотность бетона, кг × м -3; qr – теплопотери на испарение воды в порах бетона, Дж × м -3× с -1; l t – коэффициент теплопроводности бетона, Дж × м -1× °C -1× с -1 (Вт×м-1×°С-1); ct – удельная теплоёмкость бетона, Дж × кг -1× °C -1. Дифференциальное уравнение теплопроводности выражает закон сохранения энергии (первый закон термодинамики): количество подведённой теплоты (правая часть уравнения, закон Фурье) равно изменению энтальпии тела с учётом потерь тепла на испарение воды в порах бетона (левая часть уравнения). Параметры l t и ct определяются структурой, плотностью, влагосодержанием, температурой материала и продолжительностью нагрева. Зависимости l t и ct от температуры нагрева для большинства материалов с достаточной степенью точности выражаются линейными функциями (табл. 5.6): l t = А ± В (Т – Тn) = А ± Вt; (5.3) ct = С + D (Т – Тn) = С + Dt; (5.4) где l t и ct – характеристики при температуре t; А и С – соответствующие характеристики при начальной температуре Тn = 273 К (tn = 0°С); В и D – коэффициенты, учитывающие изменение характеристик l t и ct при возрастании температуры на один градус. Начальные характеристики А и С определяются стандартными методами или по справочным данным. Коэффициенты В и D, соответствующие условиям кратковременного нагрева, находят методом решения обратной задачи нестационарной теплопроводности. Согласно этому методу, параметры В и D подбирают, добиваясь наилучшей сходимости экспериментальных и расчётных кривых прогрева опытных образцов в условиях стандартного температурного режима. Для повышения точности расчёта теплотехнические характеристики применяемых материалов рекомендуется уточнять экспериментально. Из представленных в табл. 5.6 данных видно, что с ростом температуры у разных материалов коэффициент теплопроводности l t может как повышаться, так и понижаться, а удельная теплоёмкость ct всегда возрастает. Таблица 5.6 Теплотехнические параметры некоторых строительных материалов по данным ВНИИПО [25]
Начальные и граничные условия. В общем случае дифференциальное уравнение теплопроводности имеет бесконечное множество решений. Чтобы из этого множества выбрать конкретное решение, необходимо задать краевые условия: начальное условие, характеризующее распределение температуры в начальный момент времени (обычно t 0 = 20°С или Т 0 = 293 К), и граничные условия, характеризующие воздействие на поверхность окружающей среды. Граничные условия могут быть выражены тремя способами: · граничное условие 1-го рода характеризует закон изменения температуры на обогреваемой поверхности конструкции tw (t); · граничное условие 2-го рода характеризует закон изменения теплового потока, поступающего к поверхности конструкции qw (t); · граничное условие 3-го рода характеризует законы изменения температуры нагревающей среды tf (t) и коэффициента теплоотдачи a t от нагревающей среды к поверхности конструкции. Поскольку при расчёте огнестойкости закон изменения температуры среды во времени обычно известен (стандартный температурный режим испытаний), используется граничное условие 3-го рода, записанное в виде закона Ньютона-Рихмана: qw = a t (tf – tw), (5.5) где qw – плотность теплового потока, подводимого к обогреваемой поверхности, Вт × м -2; tf и tw – соответственно температура нагревающей среды и обогреваемой поверхности, °C; a t – коэффициент теплоотдачи, Вт × м -2× К -1. Теплоотдача от среды пожара к обогреваемой поверхности осуществляется путём конвекции и излучения, поэтому коэффициент теплоотдачи имеет две составляющие – конвективную a k и лучистую a R: a t = a k + a R. (5.6) При действии стандартного температурного режима рекомендуется принимать [21; 23; 28]: a k = 29 Вт × м -2× К -1; (5.7)
где с 0 – излучающая способность абсолютно чёрного тела; с 0 = 5,76 Вт × м -2× К -4; e red – приведённая степень черноты системы «огневая камера – обогреваемая поверхность»:
e f и e w – степень черноты соответственно огневой камеры печи (e f = 0,85) и поверхности конструкции; для бетона e w = 0,63, для других материалов e w определяется по справочным данным (табл. 5.6). Степень черноты e характеризует способность материала поглощать падающую на него лучистую энергию. Теоретически значение степени черноты может изменяться от нуля (для полностью отражающей поверхности) до единицы (для полностью поглощающей поверхности), однако абсолютно чёрного тела, поглощающего всё падающее на него излучение, в природе не существует. Не все поверхности, имеющие высокую степень черноты e, воспринимаются зрительно как чёрные. Например, снег не поглощает световые лучи, но поглощает тепловые, поэтому его степень черноты (e = 0,98) больше, чем у сажи (e = 0,95). Стекло, прозрачное в видимой части спектра, почти не прозрачно для тепловых лучей (e = 0,94). Коэффициенты теплоотдачи на необогреваемой поверхности [21; 23; 28]:
где Для теплопередачи в железобетонных конструкциях характерны: · внутренняя нелинейность, обусловленная зависимостью коэффициентов теплопроводности l t и теплоёмкости ct от температуры и влажности; · внешняя нелинейность, обусловленная зависимостью коэффициента теплоотдачи a t от температуры поверхности tw; · отрицательный источник тепла qr, обусловленный испарением свободной воды в порах бетона, которое происходит в интервале температур 95…170°С и замедляет прогрев конструкции за счёт поглощения некоторого количества теплоты, называемого скрытой теплотой парообразования. Точное аналитическое решение, учитывающее нестационарность процесса теплопередачи с внутренней и внешней нелинейностью при наличии внутреннего отрицательного источника тепла, не удаётся получить даже для одномерного теплового потока. Приемлемые для инженерной практики аналитические решения связаны с большим количеством упрощающих предпосылок. Разработанные аналитические методы (решение через интеграл вероятностей [28], метод термического слоя [21]) не позволяют получить расчётные формулы для сечений, которые обладают сложной конфигурацией или составлены из разнородных по теплофизическим свойствам компонентов (тавровые и двутавровые сечения, элементы пустотелые или с жёсткой арматурой). Более широкими возможностями обладают численные методы расчёта. Достаточно простым и удобным является метод конечных разностей (МКР), основанный на замене производных, входящих в дифференциальное уравнение теплопроводности Фурье, разностными отношениями. При определённых условиях решение с помощью МКР можно получить даже графически. Однако учёт поглощения тепла на испарение влаги при использовании МКР приводит к существенному усложнению алгоритма расчёта. Более предпочтительным в вычислительном отношении оказался метод элементарных тепловых балансов, отличие которого от МКР состоит в том, что уравнение Фурье не преобразуется из дифференциальной формы в конечно-разностную, а записывается заново как уравнение теплового баланса элементарного объёма D V (но уже не дифференциально малого dV) в течение заданного промежутка времени Dt. Метод элементарных балансов был предложен А.П. Ваничевым[51] для расчёта трехмерных температурных полей в материалах, теплофизические свойства которых в зависимости от температуры изменяются по линейному закону. Применительно к теплотехнической задаче расчёта огнестойкости этот метод был модифицирован А.И. Яковлевым [23; 28] с учётом влияния влажности бетона. Рассматриваемая конструкция делится на ряд элементарных объёмов (параллелепипедов со сторонами D x, D y, D z), в пределах которых закон изменения температуры принимается линейным. Для каждого элементарного объёма составляется уравнение теплового баланса: в левой части записывается тепло SD Q, поступающее в элемент через все его грани, а в правой – тепло, которое расходуется на увеличение теплосодержания элементарного объёма D H и на испарение свободной воды в порах бетона Qr: SD Q = D H + Qr. (5.12) Для наиболее простого случая – плоской односторонне обогреваемой конструкции – получаем n расчётных слоёв равной толщины D x, причём узловые точки с номерами i = 1… n находятся на границах расчётных слоёв (рис. 5.4). Принимаем, что распространение тепла происходит только вдоль оси x, тогда расстояния D y и D z можно задать единичными (1 м). Для некоторой точки с номером i, не лежащей на поверхности конструкции, записываем количество тепла D Q 1, поступающего за время Dt из полуслоя толщиной D x /2 с левой стороны, и количество тепла D Q 2, поступающего к точке i из такого же полуслоя с правой стороны, используя закон Фурье:
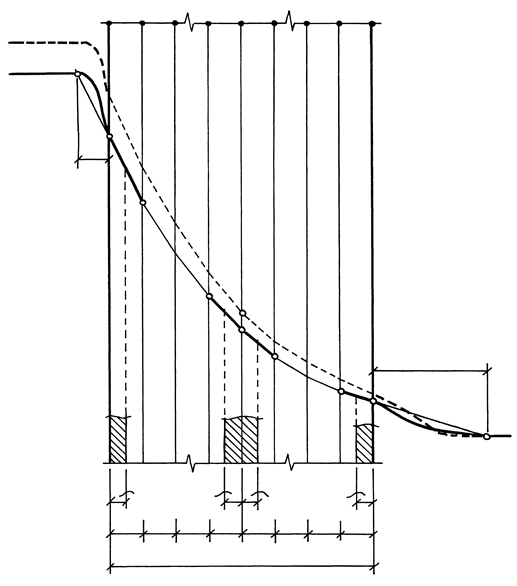
Рис. 5.4. Схема расчёта температурных полей в плоской сплошной конструкции
Учитывая линейный характер изменения температуры в пределах толщины каждого слоя и линейную зависимость коэффициента теплопроводности от температуры (5.3), получим:
Увеличение теплосодержания (энтальпии) элементарного объёма D V = D x D y D z, образованного вокруг точки i двумя полуслоями толщиной D x /2 за время Dt принимается пропорциональным повышению температуры в точке i: D H = ct , i gD t D V = ct , i r×(ti ,(t + Dt) – ti)×D V, (5.15) где ti ,(t + Dt) – температура в исследуемой точке в момент времени t + Dt; r – плотность сухого бетона, кг × м -3. Учитывая линейный характер зависимости удельной теплоёмкости от температуры (5.4), получаем D H = (C + Dti)×r×(ti ,(t + Dt) – ti)×D x D y D z. (5.16) Расход тепла на испарение воды в порах бетона
где w 0 – начальная влажность бетона, %; r – скрытая теплота парообразования воды в порах бетона; r = 2260 кДж × кг -1. Подставляя выражения (5.13)-(5.17) в уравнение (5.12) с учётом D y = D z = 1 м, получаем
откуда
где tfic – фиктивная температура, на которую снижается расчётная температура в слое за счёт расхода тепла на испарение свободной воды в порах бетона:
где tr – температура испарения воды в порах бетона; условно принимается tr = 100°С. До температуры испарения расчёт производится при tfic = 0, а после достижения бетоном температуры испарения – с учётом tfic. Для точек, лежащих на поверхности конструкции, выводятся аналогичные выражения, но с учётом граничных условий. Для определения температуры обогреваемой поверхности t 1 составляется уравнение теплового баланса слоя толщиной D x /2 возле этой поверхности:
откуда
Для необогреваемой поверхности:
откуда
(5.21) Таким образом, алгоритм расчёта температур в плоских сплошных конструкциях состоит из выражений (5.18)-(5.21). В случае двухмерного температурного поля увеличивается число слагаемых в левых частях уравнений теплового баланса. Поскольку температура в исследуемой узловой точке ti ,(t+Dt) определяется через температуры в соседних узловых точках ti –1 и ti +1 в предыдущий момент времени, величина интервала Dt должна быть такой, чтобы для любой узловой точки выполнялось условие (в случае теплового потока слева направо): ti –1> ti ,(t+Dt) > ti +1, (5.22) при невыполнении этого условия расчёт станет неверным. Максимально допустимая величина интервала Dtmax определяется для слоя с наибольшим температурным перепадом, а такой слой лежит у обогреваемой поверхности. Тогда из уравнения (5.21) получаем:
Значения Dtmax определяются при начальной и максимально возможной температурах нагрева, а для расчёта используют наименьшее из них. Как видим, максимальное значение Dtmax напрямую связано с выбранной толщиной слоёв D x. На основе представленной схемы рассчитаны температурные поля в сечениях бетонных элементов различных очертаний и размеров (рис. 5.5, 5.6); большое количество расчётных и экспериментальных данных содержится в [12; 28]. Температура нагрева арматуры принимается равной температуре бетона на уровне её центра тяжести.
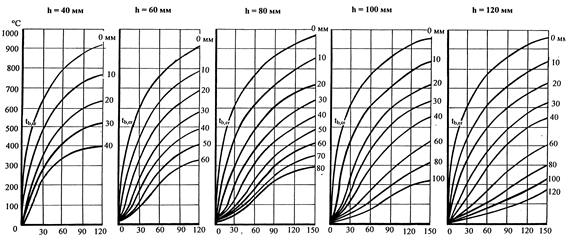
Рис. 5.5а. Кривые прогрева плит из тяжёлого бетона на силикатном заполнителе толщиной 40-120 мм [12]
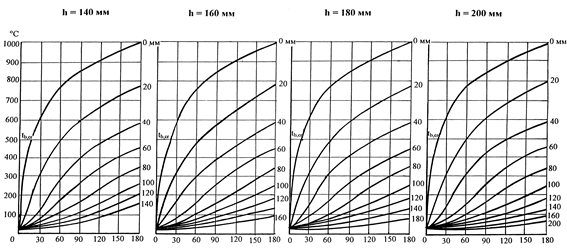
Рис. 5.5б. Кривые прогрева плит из тяжёлого бетона на силикатном заполнителе толщиной 140-200 мм [12]
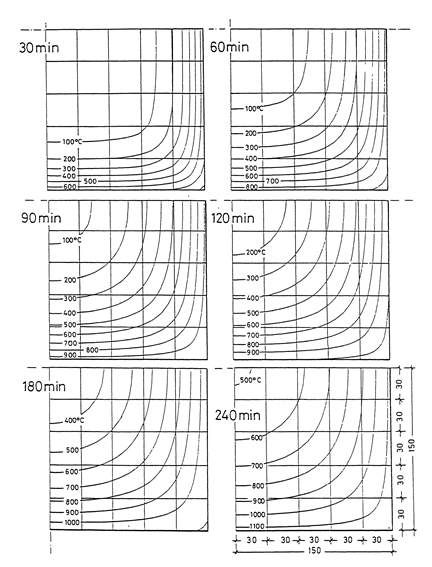
Рис. 5.6. Изотермы в бетоне колонны сечением 300х300 мм при обогреве с четырёх сторон [12]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.014 с.) |

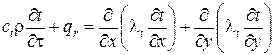 ; (5.1)
; (5.1)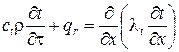 , (5.2)
, (5.2)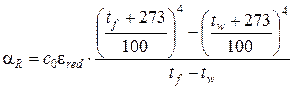 , (5.8)
, (5.8)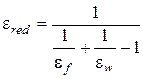 , (5.9)
, (5.9)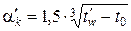 ; (5.10)
; (5.10)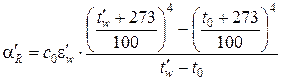 , (5.11)
, (5.11)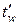 иe¢ w – температура (°С)и степень черноты необогреваемой поверхности.
иe¢ w – температура (°С)и степень черноты необогреваемой поверхности. ; (5.13.а)
; (5.13.а)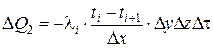 . (5.13.б)
. (5.13.б)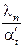
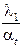

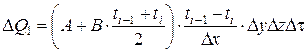 ; (5.14.а)
; (5.14.а)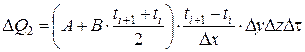 . (5.14.б)
. (5.14.б)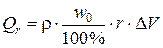 , (5.17)
, (5.17)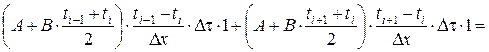
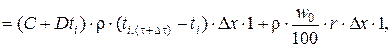
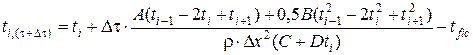 , (5.18)
, (5.18)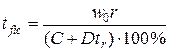 , (5.19)
, (5.19)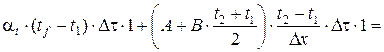
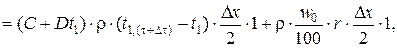
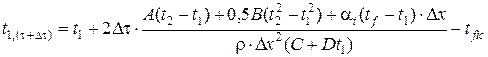 . (5.20)
. (5.20)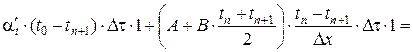
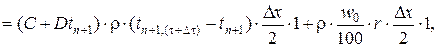
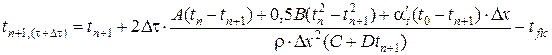 .
.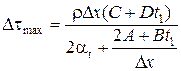 . (5.23)
. (5.23)