
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка правильности построения эпюры МСодержание книги
Поиск на нашем сайте
А. Статическая проверка. Она заключается в проверке равновесия узлов рамы, аналогично рассмотренному выше (пп. 5.3.5, 5.3.6).
Рис. 5.9. Статическая проверка эпюры М Б. Кинематическая или деформационная проверка. Она заключается в проверке отсутствия перемещений в эквивалентной системе по направлению отброшенных связей. Перемножаем суммарную “единичную” эпюру
На основе выполненных проверок убеждаемся в том, что эпюра изгибающих моментов М построена верно.
Подбор номера стального прокатного двутавра Используем условие прочности при изгибе (5.9), которое в случае одинаковых сечений всех элементов рамы можно записать в виде
По условию задания
По сортаменту прокатной стали “Балки двутавровые. ГОСТ 8239-72” (табл. 1 приложения) принимаем I № 18 а, у которого
ВНЕЦЕНТРЕННОЕ СЖАТИЕ НЕОДНОРОДНЫХ СОСТАВНЫХ СТЕРЖНЕЙ Внецентренное сжатие стержней относится к наиболее часто встречающимся в инженерной практике частным случаям сложного сопротивления. При этом виде нагружения внешние силы параллельны геометрической оси стержня и приложены с некоторыми эксцентриситетами относительно главных центральных осей инерции, а точки стержня находятся в линейном (одноосном) напряжённом состоянии, вызванном действием трёх внутренних силовых факторов: продольной силы и изгибающих моментов в перпендикулярных плоскостях. Наряду с однородными стержнями, выполненными из одного материала, иногда встречаются составные стержни, отдельные части которых изготовлены из различных материалов, в силу этого имеющие несхожие упруго-механические характеристики. Особенность расчёта таких стержней состоит в необходимости учёта упругих и прочностных свойств всего множества точек поперечного сечения. Общая формула для нормального напряжения в произвольной точке K сечения имеет вид
где Если модуль упругости остаётся постоянным в пределах конечных областей сечения, то формула (6.1) упрощается к виду
где Если стержень изготовлен полностью из однородного материала, то формула (6.2) приводится к общепринятому в инженерных расчётах выражению
При расчётах на прочность внецентренно сжатых составных стержней возникает, как правило, два типа задач: проверочный и эксплуатационный расчёты, для решения которых используются условия прочности, составленные для наиболее напряжённых точек в растянутой и сжатой областях сечения. С учётом знаков напряжений эти условия прочности можно представить в виде
где Для определения положения наиболее опасных точек необходимо построить нейтральную линию (геометрическое место точек сечения, в которых напряжение равно нулю) и провести две касательные к контуру сечения, параллельные этой линии. Нейтральная линия строится по отрезкам
Координаты приведенного центра тяжести сечения определяются согласно п. 1.1, а положение главных осей инерции – в соответствии с формулой (1.1) после замены обычных геометрических характеристик их редуцированными значениями:
Здесь После определения всех переменных и их подстановки в неравенства (6.3) вычисляются два значения силы F, из которых наименьшее принимается в качестве допускаемой нагрузки
6.1. Варианты и исходные данные домашнего задания № 6 Опора станка состоит из чугунного полуцилиндра (рис. 6.1, а), подкреплённого стальным прокатным уголком (рис. 6.1, б). Компоновка сечения стержня осуществляется путём сопряжения характерных точек фигур (0, 1,…, 9 для полукруга и 1, 2, 3 для уголка) после их поворота на углы
Рис.6.1. Составные части профиля и их ориентация: а – полукруг диаметром d; б – неравнобокий прокатный уголок
Вариант задания определяется шифром, т. е. двумя последними цифрами зачётной книжки студента. Исходные числовые данные принимаются из табл. 6.1. Модули упругости конструкционных материалов считать независимыми от марок чугуна и стали и принимать для всех вариантов: 6.2. Условие задания Для заданного варианта внецентренно сжатого стержня, составленного из элементов с различными упругими и прочностными характеристиками, определить допускаемое значение силы F, приложенной в точке, наиболее удаленной от центра тяжести сечения.
Таблица 6.1 Геометрические и прочностные параметры стержня
а – первая цифра шифра; б – вторая цифра шифра. Пример расчёта и методические указания Подготовка исходных данных и расчётной схемы Выписываем из табл. 6.1 исходные числовые данные согласно шифру. В качестве примера рассмотрим следующие данные: Согласно исходным данным поворачиваем полукруг, опирающийся на диаметр (рис. 6.1, а), на угол
Рис. 6.2. Компоновка расчётной схемы: а – поворот полукруга на 270°; б – поворот уголка на 180°; в – симметричное преобразование уголка; г – сопряжение элементов в характерных точках
Вычисляем и выписываем из таблицы сортамента (табл. 3 приложения) необходимые для дальнейших расчётов геометрические характеристики “простых” фигур. С целью уменьшения числа ошибок рекомендуется располагать полукруг согласно компоновочной схеме, а уголок – в соответствии с таблицей сортамента (рис. 6.3). Необходимо также обратить внимание на взаимную ориентацию полукруга и его центральных осей. Например, формула
Рис. 6.3. Геометрические характеристики фигур: а – полукруга; б –неравнобокого уголка Вычерчиваем в разрешённом масштабе поперечное сечение стержня на листе формата А4. Чтобы установить масштаб чертежа находим габариты сечения, используя компоновочную схему (рис. 6.2, г) и геометрические параметры фигур (рис. 6.3). Габарит сечения по ширине: Габарит сечения по высоте: Габарит формата А4 (с учётом рамки): Вычисляем масштабные коэффициенты:
Выбираем из двух значений наибольшее и округляем его до ближайшего разрешённого. В результате получаем
Рис. 6.4. Расчётная схема поперечного сечения стержня М 1:1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.23.110 (0.009 с.) |




 ;
;
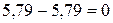 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 на окончательную эпюру М, в результате чего получаем сумму перемещений (с точностью до постоянного множителя
на окончательную эпюру М, в результате чего получаем сумму перемещений (с точностью до постоянного множителя  )
)
 ; относительная погрешность составляет
; относительная погрешность составляет  %, что указывает на высокую точность вычислений.
%, что указывает на высокую точность вычислений. .
. . Наибольший изгибающий момент находим на окончательной эпюре М (рис. 5.5, л):
. Наибольший изгибающий момент находим на окончательной эпюре М (рис. 5.5, л): 

 . Вычисляем требуемый момент сопротивления
. Вычисляем требуемый момент сопротивления ≃161,2
≃161,2  .
.
 %. Возникающее при этом перенапряжение
%. Возникающее при этом перенапряжение  % нормами расчёта разрешено.
% нормами расчёта разрешено. , (6.1)
, (6.1) – модуль упругости в т. K с координатами
– модуль упругости в т. K с координатами  ,
,  ;
;  – модуль упругости в точке с координатами
– модуль упругости в точке с координатами  ,
,  ;
;  ,
,  ,
,  – продольная сила и изгибающие моменты относительно главных осей U и V.
– продольная сила и изгибающие моменты относительно главных осей U и V. , (6.2)
, (6.2) – редукционный коэффициент в т. K, имеющий смысл относительного модуля упругости
– редукционный коэффициент в т. K, имеющий смысл относительного модуля упругости  ;
;  – редуцированная площадь всего сечения;
– редуцированная площадь всего сечения;  ,
,  – редуцированные главные моменты инерции сечения;
– редуцированные главные моменты инерции сечения;  – редукционный коэффициент для i -й области сечения;
– редукционный коэффициент для i -й области сечения;  ,
,  – осевые моменты инерции i -й области относительно приведенных главных центральных осей всего сечения; i и n – номер и число конечных областей сечения.
– осевые моменты инерции i -й области относительно приведенных главных центральных осей всего сечения; i и n – номер и число конечных областей сечения. .
. (6.3)
(6.3) ,
,  – экстремальные напряжения в сечении;
– экстремальные напряжения в сечении;  ,
,  – редукционные коэффициенты для сжатой и растянутой областей;
– редукционные коэффициенты для сжатой и растянутой областей;  ,
,  – главные эксцентриситеты точки приложения силы
– главные эксцентриситеты точки приложения силы  ;
;  ,
,  – главные координаты наиболее опасной точки в сжатой области;
– главные координаты наиболее опасной точки в сжатой области;  ,
,  – то же в растянутой области;
– то же в растянутой области;  ,
,  – квадраты радиусов инерции (
– квадраты радиусов инерции ( ,
,  );
);  ,
,  – допускаемые напряжения (с учётом знака) для сжатой и растянутой областей сечения.
– допускаемые напряжения (с учётом знака) для сжатой и растянутой областей сечения. и
и  , отсекаемым ею соответственно на главных центральных осях U и V:
, отсекаемым ею соответственно на главных центральных осях U и V: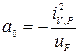 ;
;  . (6.4)
. (6.4)
 ; (6.5)
; (6.5) . (6.6)
. (6.6) и
и  ;
;  – соответственно редуцированные статические и центробежный моменты.
– соответственно редуцированные статические и центробежный моменты. .
. и
и  , как показано на рис. 6.1. Полученный составной неоднородный стержень сжимается силой F, приложенной в точке, наиболее удалённой от центра тяжести сечения.
, как показано на рис. 6.1. Полученный составной неоднородный стержень сжимается силой F, приложенной в точке, наиболее удалённой от центра тяжести сечения.


 – для чугуна;
– для чугуна; 



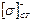


 ;
;  ; L № 8/5;
; L № 8/5; 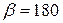 °; точки сопряжения: 7 – для полукруга; 1 – для уголка;
°; точки сопряжения: 7 – для полукруга; 1 – для уголка; 



 ° против часовой стрелки (рис. 6.2, а) и неравнобокий уголок, опирающийся на меньшую сторону (рис. 6.1, б), на угол
° против часовой стрелки (рис. 6.2, а) и неравнобокий уголок, опирающийся на меньшую сторону (рис. 6.1, б), на угол  (рис. 6.2. б). Сопряжение повёрнутых элементов сечения в точках 7
(рис. 6.2. б). Сопряжение повёрнутых элементов сечения в точках 7  и 1L без наложения фигур невозможно, поэтому осуществляем симметричное преобразование уголка по схеме рис. 6.2, в, где цифрой 1 показано исходное положение (рис. 6.2, б), а цифрами 2 и 3 – положение после симметричного (зеркального) преобразования. Условию рассматриваемого примера удовлетворяет положение 2. Соединив указанные точки элементов, получаем компоновочную схему сечения стержня (рис. 6.2. г).
и 1L без наложения фигур невозможно, поэтому осуществляем симметричное преобразование уголка по схеме рис. 6.2, в, где цифрой 1 показано исходное положение (рис. 6.2, б), а цифрами 2 и 3 – положение после симметричного (зеркального) преобразования. Условию рассматриваемого примера удовлетворяет положение 2. Соединив указанные точки элементов, получаем компоновочную схему сечения стержня (рис. 6.2. г).



 справедлива для оси, перпендикулярной диаметру, независимо от того, как она обозначена (в рассматриваемом примере это ось X).
справедлива для оси, перпендикулярной диаметру, независимо от того, как она обозначена (в рассматриваемом примере это ось X).

 мм
мм  см;
см;
 см;
см;

 ;
;

 ;
;


 .
.
 мм
мм  мм
мм  см;
см;
 мм;
мм;  мм;
мм;  мм;
мм;
 см;
см;  см;
см; 


 ;
;





 ;
;  .
. и, следовательно, масштаб чертежа М 1:1. На рис. 6.4 показана окончательная расчётная схема поперечного сечения стержня.
и, следовательно, масштаб чертежа М 1:1. На рис. 6.4 показана окончательная расчётная схема поперечного сечения стержня.



