
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр поперечных сил и изгибающих моментовСодержание книги
Поиск на нашем сайте
Названные эпюры строим для балки с двумя шарнирными опорами, т. е. для случая, рассмотренного в п. 3.3.2. Расчётная схема для построения эпюр внутренних усилий показана на рис. 3.7, а. Прежде всего, разбиваем длину балки на грузовые участки, т. е. такие отрезки, в пределах которых остаётся постоянным характер нагружения. В рассматриваемом примере получаем пять участков: CA, AD, DF, FB, BG. В пределах каждого участка проводим текущее сечение i – i (i = 1, 2, 3, …) и привязываем его абсциссой zi к началу или концу балки в зависимости от сложности учёта нагрузок, расположенных на отсечённой части балки длиной zi. Трудоёмкость вычислений можно оценить по следующей формуле:
где
Например, если для сечения 3–3 (рис. 3.7, а) рассматривать левую отсечённую часть 3–3 слева, а сечения 4–4, 5–5 справа (рис. 3.7, а). Используя определения поперечной силы (3.1) и изгибающего момента (3.2), а также их правила знаков, записываем выражения внутренних усилий для каждого грузового участка, анализируем характер их изменения по длине и вычисляем те значения, по которым можно построить графики функций (эпюры Q и М): I грузовой участок СА
графиком этой функции является квадратная парабола, которую можно построить по трём точкам – в начале (т. С), в нулевой точке эпюры
Рис. 3.7. Расчётная схема балки. Эпюры поперечных сил и изгибающих моментов
II грузовой участок АD
Замечаем, что на границе участков (т. А) выполняются ньютоновские проверки (3.3):
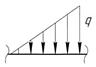
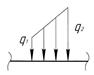
III грузовой участок DF Вычисляем предварительно интенсивность распределённой нагрузки Далее составляем выражения поперечной силы и изгибающего момента:
Замечаем, что на границе участков (т. D) выполняются ньютоновские проверки (3.3):
IV грузовой участок GB
V грузовой участок BF
Замечаем, что на границе III и V участков (т. F) выполняются ньютоновские проверки (3.3):
Относительная погрешность вычислений
При Необходимо отметить, что рассмотренные проверки особенно наглядно и просто прослеживаются на эпюрах Q и M (рис. 3.7, б, в), которые строим по полученным данным следующим образом. Проводим две базисные линии, параллельные оси балки и от них по перпендикулярам откладываем отрезки, пропорциональные значениям внутренних усилий Q и M. Для каждой эпюры выбираем масштабные коэффициенты, исходя из соображений, чтобы максимальные ординаты не превышали по своей длине четвёртую (третью) часть длины базисных линий. Для рассматриваемого примера принимаем с учётом того, что масштабный коэффициент для эпюры Q масштабный коэффициент для эпюры М На построенных эпюрах подписываем характерные значения, ставим знаки “+” или “–” и показываем абсциссы
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.171 (0.01 с.) |

 ,
,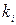 – коэффициент сложности i -го вида нагрузки;
– коэффициент сложности i -го вида нагрузки;  – число нагрузок i -го вида.
– число нагрузок i -го вида.


 , то сложность расчёта составит
, то сложность расчёта составит  . Если рассматривать правую отсечённую часть
. Если рассматривать правую отсечённую часть  , то сложность
, то сложность  . Так как
. Так как  , то сечение 3–3 легче рассчитать слева, чем справа. Исходя из высказанных соображений, в данном примере будем рассматривать сечения 1–1, 2–2,
, то сечение 3–3 легче рассчитать слева, чем справа. Исходя из высказанных соображений, в данном примере будем рассматривать сечения 1–1, 2–2,
 ; графиком этой функции является наклонная прямая, которую можно построить по двум точкам – в начале (т. С) и в конце (т. А) грузового участка:
; графиком этой функции является наклонная прямая, которую можно построить по двум точкам – в начале (т. С) и в конце (т. А) грузового участка:  кН;
кН;  кН. Так как функция
кН. Так как функция  меняет знак, то она принимает в некоторой точке участка нулевое значение. Вычисляем абсциссу этой точки
меняет знак, то она принимает в некоторой точке участка нулевое значение. Вычисляем абсциссу этой точки  ;
; ;
;  (0; 3);
(0; 3);  ;
;

 и в конце (т. А) грузового участка:
и в конце (т. А) грузового участка:  ;
; 
 ;
; 
 изгибающий момент принимает экстремальное значение на участке СА, так как 20 > (0; 15), что согласуется с дифференциальными проверками (3.4).
изгибающий момент принимает экстремальное значение на участке СА, так как 20 > (0; 15), что согласуется с дифференциальными проверками (3.4).
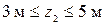
 – прямая, параллельная базисной линии, от которой откладываются ординаты;
– прямая, параллельная базисной линии, от которой откладываются ординаты; 
 – наклонная прямая:
– наклонная прямая:

 ;
;  ;
; ;
; 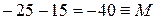 .
.
 , приложенной к балке в т. О 3 (рис. 3.7, а). Из подобия треугольников DO 3 n и DFm находим
, приложенной к балке в т. О 3 (рис. 3.7, а). Из подобия треугольников DO 3 n и DFm находим  ;
; 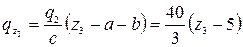 – наклонная прямая, соответствующая схеме нагружения:
– наклонная прямая, соответствующая схеме нагружения:  ;
; 
 .
.
 – квадратная парабола:
– квадратная парабола: 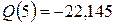 кН;
кН;  кН;
кН;  кН. Функция
кН. Функция  меняет знак, поэтому вычисляем абсциссу нуль-точки эпюры Q:
меняет знак, поэтому вычисляем абсциссу нуль-точки эпюры Q: ;
;  , отсюда находим
, отсюда находим (5; 8);
(5; 8);

 – кубическая парабола:
– кубическая парабола:
 ;
; 

 ;
;  ;
;  ;
;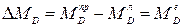 ;
;  ;
;  .
.
 – прямая, параллельная базисной линии;
– прямая, параллельная базисной линии;  – наклонная прямая;
– наклонная прямая;  ;
; 

 – наклонная прямая;
– наклонная прямая;  кН;
кН;  кН. Функция
кН. Функция  меняет знак, поэтому вычисляем абсциссу нуль-точки
меняет знак, поэтому вычисляем абсциссу нуль-точки  ;
; , отсюда находим
, отсюда находим  (4; 6);
(4; 6);

 – квадратная парабола;
– квадратная парабола; 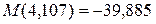

 ;
;  ;
;  ;
; ;
;  ;
;  .
. ≃0,02 % < 0,2 %.
≃0,02 % < 0,2 %. изгибающий момент принимает экстремальное значение на участке BF, так как
изгибающий момент принимает экстремальное значение на участке BF, так как  , что согласуется с дифференциальными проверками (3.4).
, что согласуется с дифференциальными проверками (3.4).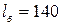 мм– длина базисной линии,
мм– длина базисной линии,  кН – наибольшее значение поперечной силы;
кН – наибольшее значение поперечной силы; 

 ;
;
 .
. нуль-точек эпюры Q (рис. 3.7, б, в).
нуль-точек эпюры Q (рис. 3.7, б, в).


