
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически неопределимые стержневыеСодержание книги
Поиск на нашем сайте
СИСТЕМЫ ПРИ РАСТЯЖЕНИИ – СЖАТИИ В инженерной практике класс статически неопределимых задач весьма обширен. Наиболее простые из них – это стержневые системы, элементы которых работают на растяжение или сжатие. Проблема статически неопределимых задач заключается в том, что они не решаются методами теоретической механики, основанными на уравнениях равновесия механических систем, состоящих из абсолютно твёрдых тел. Учёные нашли метод решения таких задач, учтя способность стержневых систем деформироваться под действием внешних нагрузок столь незначительно, что изменение размеров конструкции неразличимо невооружённым глазом. Наряду со сложностью расчета, статически неопределимые конструкции обладают другим недостатком – в них возникают “паразитические” напряжения от неточности изготовления стержней, осадки опор и изменения температуры, что, в принципе, может привести к их разрушению без приложения внешней нагрузки. Однако такие системы имеют и большое достоинство – они значительно надёжней в работе по сравнению со статически определимыми системами, так как располагают “лишними” внешними связями (опорами) и (или) внутренними связями (стержнями), удаление которых не приводит к вырождению конструкции в механизм. Сложность расчёта зависит от степени статической неопределимости
Для раскрытия статической неопределимости используют условия совместности деформаций отдельных элементов стержневой системы. Последовательность расчёта таких конструкций состоит из пяти основных частей:
г) синтез трех сторон задачи; д) условия прочности. В статической стороне задачи анализируют опорные закрепления и структуру конструкции. Записывают линейно независимые уравнения равновесия, связывающие реакции
Методом сечений получают выражения для продольных сил в каждом элементе конструкции. Вычисляют степень статической неопределимости n. В геометрической стороне задачи изображают кинематически возможную схему перемещений характерных точек стержневой системы, на основе которой устанавливают n зависимостей между абсолютными деформациями стержней ∆ l с учетом неточности их изготовления δ:
Здесь n – степень статической неопределимости; m – число стержней системы. Учитывая, что абсолютные деформации стержней составляют приблизительно 1/1000 их длины, вместо реальной схемы перемещений рассматривают упрощённую схему. Например, перемещение точки по дуге окружности, вызванное вращением стержня относительно шарнира, заменяют перемещением по касательной, что значительно упрощает составление уравнений совместности деформаций. В физической стороне задачи, используя закон Гука, выражают абсолютные деформации стержней через статические N, геометрические l, A и физические Е, α параметры с учётом температурного воздействия на элементы системы
Здесь знак “+” в левой части принимают, если на кинематической схеме j -й стержень удлиняется, и знак “–”, если j -й стержень укорачивается; Nj – продольная сила, выражение которой получено в статической стороне задачи; Ej – модуль Юнга, зависящий от материала; Синтез трёх сторон задачи заключается в совместном решении уравнений (2.2) – (2.4), в результате чего находят опорные реакции Rk и, следовательно, продольные силы Nj, выраженные через параметр площади А, который является основной неизвестной величиной в конструктивном типе расчётов на прочность:
Здесь В последней части решения задачи для нахождения неизвестного параметра площади А записывают условия прочности для каждого элемента системы в виде двойных неравенств
где Подставляя
После вычисления параметра
На заключительном этапе определяют площади всех стержней Если задача решена верно, то одно из напряжений
Рис. 2.1. Противоречивость процесса “нагружение – перемещение” 2.1. Варианты и исходные данные домашнего задания № 2
На рис. 2.2 показана конструктивная схема трёхстержневого кронштейна (фермы), задаваемая прямоугольными координатами
Рис. 2.2. Конструктивная схема стержневой системы Исходные данные, представленные в табл. 2.1 и 2.2, необходимо выбрать согласно шифру – двум последним цифрам зачётной книжки студента. Упругие и механические характеристики материалов стержней, приведенные в табл. 2.3, не зависят от шифра и принимаются одинаковыми во всех вариантах расчёта. 2.2. Условие задания
Для заданной трёхстержневой системы выполнить проектировочный расчёт на прочность: по известным нагрузкам, видам материалов и соотношениям между площадями поперечных сечений вычислить требуемые площади сечений и провести полную проверку правильности решения.
Таблица 2.1 Геометрические параметры стержневой сиcтемы
а – первая цифра шифра; б – вторая цифра шифра.
Таблица 2.2 Нагрузочные параметры стержневой системы
Таблица 2.3 Упругие и механические характеристики материалов
Пример расчёта и методические указания Подготовка исходных данных и расчётной схемы Решение задачи начинаем с выбора исходных данных из табл. 2.1 и 2.2 согласно шифру. Рассмотрим следующие параметры: Координаты узлов, мм: xА = 1568; yА = 15806; xВ = 4989; yВ = 17050; xС = 18409; yС = 21935; xD = 8409; yD = 7654. Коэффициенты: v 1 = 2; v 2 = 3; v 3 = 1. Силовое воздействие: F = 400 кН; βF =20о. Монтажное воздействие: δ 1 = –2 мм. Температурное воздействие: ∆t 3 = –20оС. Откладываем в масштабе М 1:100 координаты x, y узлов А, В, С, D в произвольно выбранной системе координат ХОУ и соединяем узел D с узлами А, В и С, в результате чего получаем трёхстержневую четырёхшарнирную конструкцию (рис. 2.2). К общему узлу D прикладываем внешнюю силу F под углом βF к горизонтальной оси Х. Показываем в масштабе М 10:1 неточность изготовления одного из стержней с учётом знака δ. При положительном δ стержень изображаем длиннее проектного, а при отрицательном δ – короче. Для рассматриваемого примера расчётная схема показана на рис. 2.3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.90 (0.011 с.) |

 , под которой понимают разность между числом неизвестных реакций и линейно независимых от них внутренних усилий
, под которой понимают разность между числом неизвестных реакций и линейно независимых от них внутренних усилий  и числом независимых уравнений равновесия
и числом независимых уравнений равновесия  , т.е.
, т.е. . (2.1)
. (2.1) анализ
анализ . Например, для плоской системы сходящихся сил составляют два уравнения равновесия
. Например, для плоской системы сходящихся сил составляют два уравнения равновесия
 (2.2)
(2.2) (i =1,2,3,…, n; j =1,2,3,…, m). (2.3)
(i =1,2,3,…, n; j =1,2,3,…, m). (2.3)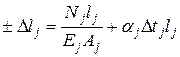 . (2.4)
. (2.4) – площадь сечения (
– площадь сечения ( – коэффициент, А – параметр);
– коэффициент, А – параметр);  – длина стержня;
– длина стержня;  – температурный коэффициент линейного расширения;
– температурный коэффициент линейного расширения;  – изменение температуры.
– изменение температуры.
 (2.5)
(2.5)
 – коэффициенты, зависящие только от внешних сил F;
– коэффициенты, зависящие только от внешних сил F; 
 – коэффициенты, зависящие от монтажных δ и температурных ∆t воздействий; k – номер опорной реакции; j – номер элемента конструкции.
– коэффициенты, зависящие от монтажных δ и температурных ∆t воздействий; k – номер опорной реакции; j – номер элемента конструкции. (
( = 1, 2, 3,…, m), (2.6)
= 1, 2, 3,…, m), (2.6) и
и  – допускаемые напряжения при сжатии и растяжении.
– допускаемые напряжения при сжатии и растяжении. и
и  в неравенства (2.6), находят m значений параметра А с учётом знака коэффициента
в неравенства (2.6), находят m значений параметра А с учётом знака коэффициента  если
если 
 если
если  (2.7)
(2.7) из всех неравенств (2.7) выбирают наибольший из них в качестве окончательного значения
из всех неравенств (2.7) выбирают наибольший из них в качестве окончательного значения .
. и абсолютные деформации по формуле (2.4). Затем производят проверку правильности решения задачи.
и абсолютные деформации по формуле (2.4). Затем производят проверку правильности решения задачи. должно равняться допускаемому
должно равняться допускаемому  , а остальные – меньше допускаемых. Найденные реакции должны удовлетворять условиям равновесия, а удлинения (укорочения) стержней – условиям совместности деформаций элементов системы. Реальная схема перемещений характерных точек конструкции не должна входить в противоречие с действующими нагрузками, как, например, показано на рис. 2.1.
, а остальные – меньше допускаемых. Найденные реакции должны удовлетворять условиям равновесия, а удлинения (укорочения) стержней – условиям совместности деформаций элементов системы. Реальная схема перемещений характерных точек конструкции не должна входить в противоречие с действующими нагрузками, как, например, показано на рис. 2.1.

 характерных узлов А, В, С, D. Внешняя нагрузка в виде сосредоточенной силы F приложена к общему узлу D, образуя угол
характерных узлов А, В, С, D. Внешняя нагрузка в виде сосредоточенной силы F приложена к общему узлу D, образуя угол  с осью Х. Прочность и жёсткость конструкции определяется видом материала стержней (сталь, чугун, медь) и соотношениями между площадями поперечных сечений
с осью Х. Прочность и жёсткость конструкции определяется видом материала стержней (сталь, чугун, медь) и соотношениями между площадями поперечных сечений  . При решении задачи необходимо учесть, что один из стержней изготовлен неточно на величину δ, а у другого стержня после сборки конструкции температура изменяется на величину ∆t.
. При решении задачи необходимо учесть, что один из стержней изготовлен неточно на величину δ, а у другого стержня после сборки конструкции температура изменяется на величину ∆t.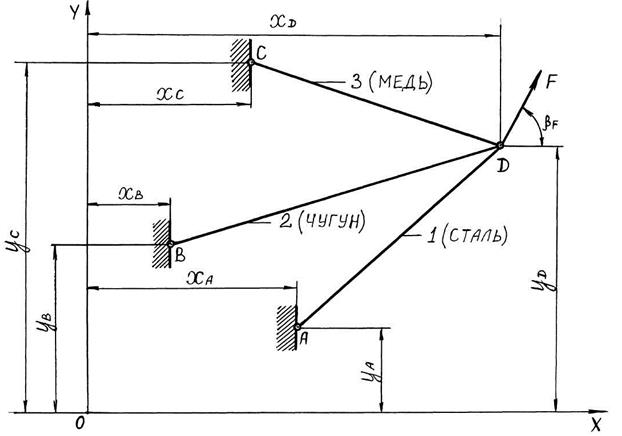









 , гр.
, гр.








