
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение координат центров тяжестей “простых” фигурСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
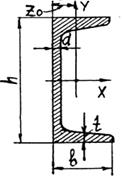
И всего поперечного сечения Выбираем произвольную правовинтовую систему координат XOY и из центра тяжести каждой “простой” фигуры Сi проводим собственные центральные оси XCi, YCi, параллельные осям Х, Y. Показываем координаты центров тяжестей каждой фигуры хCi, yCi относительно вспомогательной системы XOY и вычисляем их значения, используя характерные размеры элементов с учётом их расположения в сечении (рис. 1.5):
Рис. 1.4. Эскизы фигур и их характеристики Определяем координаты центра тяжести поперечного сечения в системе осей XOY по формулам (1.3):
Рис. 1.5. Поперечное сечение стержня (М 1:2) Откладываем в масштабе отрезки хC, уC и проводим центральные оси ХС, YС, на пересечении которых получаем центр тяжести сечения С (рис. 1.5). Вычисляем координаты центров тяжестей “простых” фигур относительно центральных осей всего сечения XC, YC, используя формулы
Проверяем выполнение основного свойства центральных осей, для которых статические моменты площади должны равняться нулю:
Учитывая малую погрешность вычислений, заключаем, что координаты центра тяжести поперечного сечения найдены верно (при условии, что правильно определены координаты xCi, yCi).
Определение осевых и центробежного моментов инерции сечения относительно центральных осей ХC, УC Находим моменты инерции “простых” фигур относительно собственных центральных осей. Сравнивая расположение фигур и осей на чертеже (рис. 1.5) и эскизах (рис. 1.4), замечаем, что
Знак центробежного момента инерции уголка в сечении определяем, представив интеграл по всей площади в виде суммы трёх подинтегралов (рис. 1.6):
Из рисунка видно, что первый и третий подынтегралы отрицательны и значительно превышают по модулю второй (положительный) подынтеграл. Следовательно, при данном расположении уголка его центробежный момент инерции отрицателен. Вычисляем моменты инерции “простых” фигур относительно центральных осей ХC, YC всего сечения. Используем формулы для преобразования моментов инерции при параллельном переносе с центральных осей фигуры ХCi, YCi на параллельные им оси ХC, YC (рис. 1.5):
Рис 1.6. Определение знака центробежного момента инерции уголка
Для первой фигуры – двутавра:
Для второй фигуры – уголка:
Для третьей фигуры – листа:
Для четвёртой фигуры – швеллера:
Находим центральные моменты инерции поперечного сечения, произведя суммирование по всем составляющим фигурам:
Определение положения главных центральных осей Инерции сечения Используем формулу (1.1):
Так как угол получился отрицательным, откладываем его по ходу часовой стрелки и проводим главные оси U и V (рис. 1.5). Вычисляем значения тригонометрических функций
Проверяем основное тригонометрическое тождество
Определение главных центральных моментов Инерции сечения Используем формулы (1.2):
Проверяем правильность вычислений. А. Условие стационарности суммы осевых моментов инерции при повороте осей: JXC + JYC = 4916+2602 = 7518 Б. Условие экстремальности главных осевых моментов инерции: JU = 5624 > { JXC = 4916 ∩ JYC = 2602} – максимум; JV = 1894 < { JXC = 4916 ∩ JYC = 2602} – минимум. В. Основное свойство главных осей: Выше мы вычислили
Определение моментов сопротивления Относительно главных осей Осевые моменты сопротивления характеризуют изгибную прочность стержней (балок) с заданными геометрическими параметрами сечения. Вычисляются они как отношения моментов инерции к расстояниям от главных осей до наиболее удаленных от них точек сечения. Чтобы найти опасные точки, проведём по две пары касательных, параллельных главным осям U, V (по разные стороны от осей), и выберем те точки касания, которые наиболее удалены от главных осей (устанавливаем визуально или с помощью линейки). В рассматриваемом примере от оси V наиболее удалена т. А, а от оси U – т. В (рис. 1.5).
Вычисляем главные координаты опасных точек, используя формулы аналитической геометрии:
где xA, yA, xB, yB, xC, yC – координаты точек А, В и центра тяжести C во вспомогательной системе координат XOY. Из рис. 1.5 находим
В п. 1.3.2 мы вычислили хC = 8,86 см; уC = 19,33 см. Подставляя в формулы эти значения, получаем
Знаки “минус” показывают, что точки удалены от главных осей в сторону отрицательного направления осей U и V. Определяем осевые моменты сопротивления
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 802; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.167.244 (0.011 с.) |

 ;
;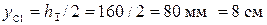 ;
; мм = 3,23 см;
мм = 3,23 см; мм = 17,42 см;
мм = 17,42 см; ;
; ;
; þ
þ  ;
; þ – z 0,þ
þ – z 0,þ 



 b = 200 мм;
h = 20 мм;
А = bh = 20 ∙ 2 = 40 см2;
JX = bh 3/12 = 20 ∙ 23/12 = 13,3 см4;
JY = b 3 h /12 = 203 ∙ 2/12 = 1333см4;
JXY = 0.
b = 200 мм;
h = 20 мм;
А = bh = 20 ∙ 2 = 40 см2;
JX = bh 3/12 = 20 ∙ 23/12 = 13,3 см4;
JY = b 3 h /12 = 203 ∙ 2/12 = 1333см4;
JXY = 0.

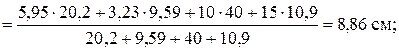



 ;
;  (i = 1 – 4):
(i = 1 – 4): ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
;  .
.
 ; относительная погрешность вычислений
; относительная погрешность вычислений  ⋍ 0,1 %.
⋍ 0,1 %.
 ; относительная погрешность вычислений
; относительная погрешность вычислений  ⋍ 0,2 %.
⋍ 0,2 %. ;
;  ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;  ;
;
 ;
;  ;
;  .
. .
.
 ;
;  ;
;  .
. ;
; ;
; .
. ;
; ;
; .
. ;
;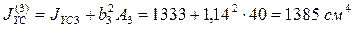 ;
; .
. ;
; ;
;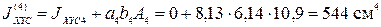 .
.
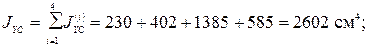

 .
. ;
;  ;
;  ;
; ;
; 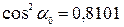 ;
;  .
. ;
;  – верно.
– верно.
 ;
;
 ;
;
 .
. ; JU + JV = 5624+1894 = 7518
; JU + JV = 5624+1894 = 7518  .
. . Относительная погрешность
. Относительная погрешность
 ;
; ,
, ;
;  ;
; ;
;  .
. см;
см; см.
см. ;
;  .
.


