
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение длительности сигналаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для определения длительности сигнала пользуются калибратором длительности. Он запирает электронный луч через определенные промежутки и создает метки времени. По числу меток можно определить длительность сигнала. Поставьте частоту звукового генератора 103 Гц. Соедините проводом «выход» генератора с «входом «Y» осциллографа. Переключатели на осциллографе поставьте в положение: «Род работы» — «непр», «Род синхронизации» — «внутр», «Развертка» - 2000 Гц (по внутр. шкале) «Метки» - 20 мксек, Включив тумблеры «сеть» генератора и осциллографа и регулируя ручками «частота плавно» и «синхронизация», получите на экране пунктирную синусоиду. Окончательно настройте ее на четкое изображение, слегка вращая лимб «частоты» звукового генератора около 103 Гц. Сосчитайте количество «n» меток за один период развертки и определите длительность Т1 =n • 20 • 10-6 сек, Подсчитайте частоту
Проделайте те же измерения на частоте генератора 550 Гц и определите новые значения T1 и n2. Измерьте период колебаний на частоте генератора, указанной преподавателем. Полученные результаты занесите в таблицу №4. Переключите тумблер «метки» в положение «выкл.». Выключайте осциллограф и генератор тумблером «сеть». Внимание! Данная лабораторная работа имеет большой объем теоретического материала и практических заданий. В этой связи она может, по указанию преподавателя, выполняться по частям или же какие-либо разделы могут быть им исключены. Это согласование необходимо провести заранее.
Таблица №4.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Как устроена электроннолучевая трубка? 2. Почему для временной развертки используется генератор пилообразных колебаний? 3. Как создаются «метки» времени? 4. Как определяется величина поданного сигнала. Что называется амплитудным, импульсным и эффективным напряжением? 5. Постройте фигуру Лиссажу для ux =uy при j0 =0. 6. Объясните способ получения сдвига фазы между двумя синусоидальными процессами, использованный в работе.
Рекомендуемая литература. 1. Савельев И.В. Курс общей физики.(в 3-х т.)М.,Наука.1979-1989 г. т.1,2. 2. Детлаф А.А., Яворский Б.М. Курс физики.М.,В.школа.1989, 2000 г. 3. Т.И. Трофимова. Курс физики. М. В. школа. 2000 г.
Работа №72 СНЯТИЕ КРИВОЙ НАМАГНИЧИВАНИЯ И ПЕТЛИ ГИСТЕРЕЗИСА ФЕРРОМАГНИТНЫХ ВЕЩЕСТВ С ПОМОЩЬЮ ОСЦИЛЛОГРАФА
Цель работы. Получить на экране осциллографа петлю гистерезиса, измерить ее параметры, снять кривую намагничивания. Приборы и принадлежности: электронный осциллограф, звуковой генератор, измерительная панель, калька, миллиметровая бумага (заготовить дома заранее), соединительные провода (получить у лаборанта).
Введение
Все вещества обладают магнитными свойствами, которые обнаруживаются при помещении их во внешнее магнитное поле B 0. В этом поле они намагничиваются и создают дополнительное магнитное поле B ’. Результирующее поле в веществе будет равно:
B = B 0+ B ’.
Рассмотрим причину возникновения дополнительного магнитного поля. Известно, что контур с током характеризуется магнитным моментом
pm=IS,
где I - сила тока в контуре; S - площадь, ограниченная контуром. Электрон в атоме движется вокруг ядра, поэтому его можно рассматривать как некоторый контур с током и рассчитать его орбитальный магнитный момент pl. Классический расчет для круговой орбиты дает
где e -заряд электрона; u - его линейная скорость; r -радиус орбиты. Если учесть условие стационарности орбит электрона в теории атома, данной Бором (
Величина Более точный расчет орбитального магнитного момента электрона в атоме дает квантовая механика. Согласно ее результатам
pl = где l – целое число, например, 0,1,2,.... Кроме орбитального, электрон обладает еще собственным (спиновым) магнитным моментом, связанным с существованием у него собственного момента количества движения (спина). Спиновый магнитный момент электрона равен ps= Полный магнитный момент атома p равен векторной сумме магнитных моментов всех составляющих его частиц. При этом сложение происходит по квантовым законам. Ядра атомов также обладают магнитными моментами, но по сравнению с магнитными моментами электронов ими можно пренебречь.
Магнитное поле вещества зависит от ориентации магнитных моментов атомов. Если все моменты расположены хаотично, то магнитное поле B ’ отсутствует. При частичной или полной упорядоченности магнитных моментов в веществе создается магнитное поле B ’. Характеристикой магнитного состояния вещества является вектор намагничения или намагниченность J.По определению J= где DV- объем, в пределах которого суммируются полные магнитные моменты атомов. Будем исходить из того, что магнитное поле в веществе создается макротоками, т.е. токами в проводниках I, и микротоками I¢, определяющими величину J. Таким образом, полная индукция является функцией макротоков и намагниченности вещества. Расчет индукции B сложен, так как B зависит не только от свойств вещества, но и от формы и размеров образца. Во многих случаях расчет упрощается введением еще одной характеристики магнитного поля - вектора напряженности магнитного поля H, по определению равной
где mo - магнитная постоянная. Вектор H обладает тем свойством, что его циркуляция в произвольном поле и в любых магнитных веществах зависит только от макротоков I,
(закон полного тока в магнитных средах, токи I протекают через площадь, охватываемую контуром “k”). В вакууме, где нет микротоков,
H = B /mo.
Если для данного вещества экспериментально получить зависимость J = J (H), которая одинакова для образцов любой формы и размеров, и рассчитать по формуле (2) H, то на основании уравнения (1) можно найти индукцию магнитного поля в веществе. Экспериментально наиболее просто J = J (H) определяется для образца в виде тороида, на который равномерно нанесены витки провода. Действительно, если в проводнике идет ток I, а общее число витков составляет N и длина тороида L, то на основании формулы (2) получаем
откуда H = NI/L, (3)
т.е. величина H может быть легко рассчитана.
Рис. 1 Рис. 2 Измеряя для каждого H величину намагниченности J, находим зависимость J = J (H) (рис.1). На рисунке Js есть намагниченность насыщения, соответствующая случаю, когда все магнитные моменты атомов ориентированы по направлению магнитного поля. Выразим связь между J и H в виде
J =c H, (4)
где c - магнитная восприимчивость вещества. Тогда из формул (1) и (4) следует:
B =mo H +mo J =mo H (1+c). (5)
Величину (1+c) обозначают m и называют магнитной проницаемостью вещества. Следовательно, связь между B и H записывается в виде B =mom H. Для ферромагнитных веществ график зависимости B=B(H) дан на рис.2. Кроме того, на рис.2 дается зависимость m от H. Как видно из графика, с увеличением H индукция увеличивается. Рост индукции B в веществе после достижения намагниченности насыщения Js объясняется дальнейшим увеличением напряженности поля (см. формулу (5)). По своим магнитным свойствам ферромагнетики существенно отличаются от пара- и диамагнетиков*. В частности, их относительная магнитная проницаемость может достигать величины 104¸105, они могут обладать также и остаточной намагниченностью. ______________ * Более подробно с особенностями ферромагнетиков можно ознакомиться по литературе, приведенной в разделах "Ферромагнетизм, намагничивание и т.д." в книге: Физический энциклопедический словарь/ Под ред. А.М. Прохорова - М.: Сов. энциклопедия, 1984. -944 с.
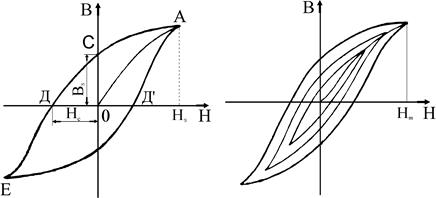
Эти особенности невозможно объяснить с позиции классической физики. Объяснение явления ферромагнетизма дала лишь квантовая механика. В квантовой теории считается, что под действием так называемых обменных сил магнитные моменты отдельных атомов должны выстраиваться параллельно друг другу. При этом в кристалле образуются области спонтанного, самопроизвольного намагничивания, которые носят название доменов. В пределах каждого домена (размер домена порядка 1–10 мкм) ферромагнетик намагничен до насыщения. В отсутствии внешнего поля в ферромагнетике, как правило, наблюдается образование большого количества доменов. Такая ситуация энергетически более выгодна по сравнению со случаем, когда имеется, например, лишь один домен, поскольку сведено до минимума рассеяние магнитного поля в пространство вне ферромагнетика, причем направления магнитных моментов для разных доменов различны, так что суммарный момент может быть равен нулю. Все зависит от предыстории образца. Остановимся теперь на объяснении хода зависимости B = f (H) для ферромагнетика. Зависимость B от H для ферромагнетиков имеет сложный вид. Если после достижения намагниченности насыщения Hs уменьшать напряженность поля, то индукция будет изменяться иначе, чем это получалось при первоначальном намагничивании. На графике (рис.3) это изменение характеризуется участком АС. Индукция, получаемая при H =0, называется остаточной индукцией Bs. Изменение направления намагничивающего поля приводит к размагничиванию ферромагнетика (участок CD). Величина Hc (участок OD) называется коэрцитивной силой. Дальнейшее увеличение поля H приводит к намагничиванию в противоположном направлении (участок DE). Новое изменение направления и величины поля дает изменение индукции, характеризуемое участками ED¢A. В целом получается замкнутый цикл, называемый петлей гистерезиса. Если первоначальное намагничивание не доводить до насыщения (H<Hs) и провести все операции для получения цикла, то получим петли гистерезиса меньших размеров (рис.4).
Рис. 3 Рис. 4
Такие петли называются частными циклами. Вершины частных циклов петель гистерезиса находятся на кривой намагничивания. С позиции теории ферромагнетизма намагничивание ферромагнетика качественно можно представить как переориентацию доменов в направлении внешнего поля по мере его увеличения, причем сначала происходит смещение границ доменов и увеличение тех доменов, вектор магнитного момента которых составляет с вектором H внешнего магнитного поля острый угол. По мере увеличения поля начинают преобладать процессы поворота вектора магнитного момента внутри домена. При сильных полях магнитные моменты всех доменов ориентируются по полю. Это характерно для состояния насыщения. Поскольку процесс переориентации доменов в процессе намагничивания необратим, то наблюдается гистерезис (гистерезис - отставание, задерживание, запаздывание). В частности, остаточное намагничивание образца объясняется тем, что при снятии внешнего поля направление магнитных моментов доменов не может принять такое положение, при котором их сумма равна нулю. При увеличении напряженности магнитного поля, имеющей противоположное направление, происходит переориентация доменов в другом направлении.
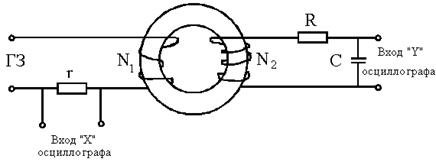
Практическая часть Метод измерения и схема установки. Получение петли гистерезиса и проведение необходимых измерений для определения B и H осуществляется в данной работе на электронном осциллографе. Схема установки дана на рис. 5.
Рис.5
Переменное напряжение от звукового генератора (ГЗ) подключается к виткам N 1 намагничивающей обмотки тороида, укрепленного на панели. На панели размещены сопротивление r, включенное в цепь намагничивающей обмотки, а также сопротивление R и конденсатор C, находящиеся в цепи вторичной обмотки N 2. Напряжение Ux = Ir подается на горизонтально отклоняющие пластины ² x ² электронного осциллографа. Напряженность магнитного поля в тороиде пропорциональна силе тока I (см. формулу (3)), следовательно, отклонение электронного луча по горизонтали (вдоль оси x) пропорционально напряженности поля H:
Индуцированная ЭДС во вторичной обмотке N 2 периодически заряжает конденсатор C до напряжения Uy, которое подается на вертикально отклоняющие пластины ² y ² электронного осциллографа. Отклонение луча по вертикали, пропорциональное Uy, связано с величиной индукции B поля в сердечнике тороида. Действительно, ЭДС индукции равна
e = - N2S
где S - площадь сечения тороида; N 2 число витков вторичной обмотки тороида. Для того, чтобы получить сигнал, пропорциональный индукции магнитного поля, используется интегрирующая цепочка RC, удовлетворяющая условию RC > T (T - период переменного тока). При R >>
Напряжение
Uc = Uy; Uy =
Из вышеприведенных соотношений следует, что
Uy = -
Таким образом, на ² x ² пластины осциллографа подается напряжение, пропорциональное H, а на ² y ² пластины пропорциональное B. На экране осциллографа получается фигура, с помощью которой можно определить петлю гистерезиса B = B (H). За один период изменения Ux и Uy след электронного луча опишет всю фигуру петли гистерезиса, а за каждый последующий период ее повторит, поэтому на экране осциллографа видна неподвижная картина.
Величины H и B определяются из соотношений H = ax и B = by, где x и y - координаты соответствующей точки петли, выраженные в миллиметрах, а a - цена деления шкалы осциллографа по горизонтали в амперах на миллиметр; b - цена деления шкалы осциллографа по вертикали в теслах на миллиметр. Величины a, b определены опытным путем и указаны на установках.
Порядок выполнения работы
1. Собрать схему установки (см. рис. 5). 2. Включить приборы и получить на экране осциллографа изображение петли гистерезиса. Первоначальное положение ручек управления осциллографом и звуковым генератором для получения петли дается на установке. Внимание. После настройки установки и получении на экране осциллографа изображение петли гистерезиса нельзя изменять положения ручек настройки осциллографа и звукового генератора. 3. После получения на экране осциллографа петли y = y (x) (размеры петли указаны на установке) провести измерения координат семи точек петли для участка АСDE (см. рис.3). Если отсутствует прозрачная миллиметровая сетка, то к экрану осциллографа можно приложить кальку или бумажный лист и скопировать изображение петли гистерезиса. Затем, воспользовавшись линейкой или миллиметровой бумагой, надо измерить координаты точек. Результаты измерений занести в табл.1. После расчета H и B построить график. На графике участок ED ¢ A строится симметрично участку ACDE (см. рис.3 ). Можно и сразу заготовить таблицу для снятия большего количества точек, например, 15-ти точек. 4. Для получения кривой намагничивания необходимо измерить координаты вершин петли y = y (x) при уменьшенных напряжениях, подаваемых от звукового генератора. Остальные параметры выбранного режима работы осциллографа и генератора изменять нельзя. Таблица 1
Следует измерить координаты вершин семи петель различных размеров, постепенно сводя петлю в точку, уменьшая выходное напряжение звукового генератора. 5. По данным измерений, сведенных в табл. 2, построить кривую намагничивания. Графики рекомендуется строить на миллиметровой бумаге.
Таблица 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 713; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.36.138 (0.013 с.) |

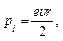
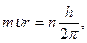 где n =1,2,3,...), то орбитальный магнитный момент электрона можно записать так:
где n =1,2,3,...), то орбитальный магнитный момент электрона можно записать так: в,
в,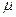 в = 0,927 10-23 А×м2 служит единицей измерения магнитных моментов микрочастиц; ее называют магнетоном Бора.
в = 0,927 10-23 А×м2 служит единицей измерения магнитных моментов микрочастиц; ее называют магнетоном Бора.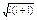
 ,
,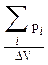 ,
, (1)
(1) H d l =
H d l = 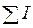 , (2)
, (2)
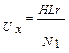 . (6)
. (6)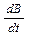 (7)
(7)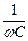 ток в цепи вторичной обмотки
ток в цепи вторичной обмотки .
.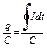 .
.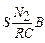 .
.


