
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимірювання частотних та амплітудних характеристик сигналівСодержание книги
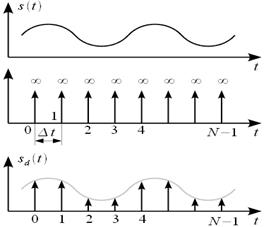
Поиск на нашем сайте Одним із найважливіших питань аналізу стану технічних каналів витоку інформації є вимірювання інформаційних характеристик діючих сигналів. При цьому, у першу чергу, необхідне уявлення та розуміння фізичних принципів передачі інформації. Важливим питанням за приймання та передавання сигналів є процес узгодження характеристик джерела/приймача сигналу з середовищем передачі. Одним із методів такого узгодження є застосування модуляції – процесу зміни одного чи декількох параметрів носійного коливання за законом інформаційного сигналу. Як носійні можуть бути використані коливання різної форми (прямокутні, трикутні тощо), проте найчастіше застосовуються гармонійні коливання. Залежно від того, який із параметрів носійного коливання змінюється, розрізняють вид модуляції (амплітудна (рис. 2.1,а), фазова (рис. 2.1,б), частотна (рис. 2.1,в) тощо). Модуляція дискретним сигналом (може приймати лише кінцеве число значень) називається цифровою модуляцією або маніпуляцією. У процесі приймання та аналізу сигнал проходить дискретизацію, тобто перетворення із аналогового (неперервного) у сигнал із скінченним числом його значень (рис. 2.1.г). При цьому для вибору інтервалу чи частоти дискретизації використовується теорема Котельникова [11, 12]:
Подання сигналу у вигляді дискретних відліків, які, у свою чергу, квантуються та оцифровуються, дає можливість обробки сигналів цифровими способами. Оскільки на приймальній стороні не відомі початкові параметри сигналу, що приймається, то для виключення похибки над прийнятим сигналом виконують низку додаткових обчислень: – розраховують два добутки X та Y між прийнятими коливаннями Uс(t) та косинусоїдальним
– отримують квадрат набутих значень X та Y, знаходять їхню суму й обчислюють квадратний корінь.
Рисунок 2.1 – Приклади аналізованих сигналів
З формули (2.3) видно, що значення функції Z (t) не залежить від початкової фази сигналу та за нормування
Після проведення даних операцій можливе визначення амплітудних характеристик аналізованих сигналів [13]: – значення максимальної амплітуди; – значення усередненої амплітуди (див. рис. 2.1,д):
де n – кількість імпульсів в аналізованій послідовності;
При цьому, середньоквадратича помилка може бути визначена за формулою:
Середньоквадратичний рівень сигналів/шумів:
де Т – інтервал вимірювання;
Середнє значення сигналів:
Розглянемо вимірювання даних характеристик на прикладі вимірювального комплексу «АКОР-3ПК». Апаратура, що входить до комплексу, забезпечує виконання наступних функцій. Перетворювач радіочастот (ПРЧ) забезпечує приймання сигналів у діапазоні частот 0,01 – 3000 МГц і перетворює їх у другу проміжну частоту 10,7 МГц із смугою пропускання не менше 4 МГц. Крім того, ПРЧ забезпечує детектування сигналів, що приймаються, для прослуховування. Блок АЦСП разом з БПО синтезує частоти у смузі 4 МГц із кроком 20 кГц і перетворюють сигнал із другою проміжною частотою у форму квадратури, забезпечують швидкість сканування 200 МГц/с, тим самим забезпечуючи перегляд робочого діапазону вимірювача (з урахуванням часу перемикання БПРЧ через 4 МГц) зі швидкістю 80 МГц/с у діапазоні частот 30…3000 МГц. У діапазонах частот 0,01…12,5 МГц і 12,5…44 МГц крок перебудови складає 30 і 200 кГц, відповідно. Даний блок забезпечує також третє перетворення частоти у «нульову», фільтрацію сигналу і формування двох каналів квадратури та забезпечує обчислення двох функцій взаємної кореляції X та Y між прийнятими коливаннями та формованими блоком косинусоїдальним і синусоїдальним сигналами. Перетворення частоти у «нульову» означає перетворення у смугу низькочастотного діапазону від 0 Гц до верхньої частоти цієї смуги. Блок аналого-цифрового сигнального процесора (АЦСП) проводить фільтрацію та перетворення аналогових сигналів, що надходять двома каналами X та Y, у цифрову форму з тактовою частотою 156 кГц й керує всіма пристроями, вбудованими у ЦБК. Дані сигнали виводяться у вікні Аналізатор/Квадратура у Головному вікні програми, вид яких наведено на рис. 2.2.
Рисунок 2.2 – Вид вхідного сигналу після обробки квадратури
Персональний комп’ютер (ПЕОМ) виконує наступні функції: а) обробляє оцифровані сигнали X та Y, таким чином, реалізуючи оптимальний виявляч, вимірювання амплітуд безперервних й імпульсних сигналів і шумів. Значення амплітуди Z (t) виводиться у вікні програми Аналіз/Амплітуда у Головному вікні програми, вид якої наведено на рис. 2.3
Рисунок 2.3 – Вид вхідного сигналу у вікні Амплітуда
б) керує апаратурою вимірювача, обробляє сигнали за допомогою спеціального програмного та математичного забезпечення, проводить розрахунок вимірюваних параметрів сигналів, ухвалює логічні рішення при роботі вимірювача в автоматичному режимі, відображає сигнальну й іншу інформацію, протоколює отримані результати. Блоком високочастотного комутатора (БВЧК) є швидкодіючий широкосмуговий ВЧ – комутатор, який служить для підключення до вимірювача додаткових антен для виявлення сигналів. У вимірювальному тракті вимірювача використовується антенний вхід ANT2.4 блока для підключення внутрішнього калібратора. Телефони (навушники) призначені для прослуховування вимірюваних сигналів. Вимірювання сигналів проводиться в автоматичному режимі за списком частот або на фіксованій частоті за командою оператора. При виборі режимів вимірювання потрібно керуватися наступним: – для імпульсних й амплітудно-модульованих сигналів використовуються режими вимірювання «P», «SA», середнє значення (режим "S"), максимальна амплітуда, усереднена амплітуда, середнє значення, ефективне й амплітудне значення; – для немодульованих сигналів використовуються режими «F», «А»; – для вимірювання шумів використовується режим «середньоквадратичне значення» («SK»); – для імпульсних сигналів використовується режим «квазіпікове значення» за ГОСТ Р 51319 (ГОСТ 11001-80) [14]. Спектральне описування інформаційного повідомлення має таке обґрунтування. Для кожної реалізації сигналу, що являє собою реалізацію x 1(t 1) випадкового процесу обчислюється спектральна функція за допомогою перетворення Фур’є [15, с. 32]:
За теоремою Парсеваля обчислюється середня (за час реалізації T р) потужність:
де функція
є функцією щільності потужності за частотою. Усереднення цієї функції за всіма реалізаціями повідомлення дає спектральну характеристику процесу, яку називають енергетичним спектром:
Знання енергетичного спектра сигналу дозволяє обчислити середню (за реалізаціями) потужність, що міститься у заданому діапазоні частот від ω1 до ω2):
де подвоєння інтегралу необхідно внаслідок формального визначення перетворення Фур’є в області позитивних та негативних частот. Спектр
що називають одностороннім енергетичним спектром. Для ергодичного процесу автокореляційна функція може бути знайдена по одній, теоретично нескінченній реалізації:
Функція rX (τ) характеризує у середньому частоту коливань у реалізації повідомлення. Важливі властивості автокореляційної функції: В інженерній практиці інтеграл замінюється сумою, а максимальне значення аргументу τ, τмах обирається порядку 0,1 T р. Часто достатньою характеристикою автокореляційної функції є її ширина τ0, що називається інтервалом кореляції. При τ > τ0 rx (τ) ≈ 0. Це означає відсутність лінійного зв’язку між X (t) та X (t + τ). Величина τ0 визначається як половина ширини основи прямокутника, висота якого дорівнює rx (0):
Між енергетичним спектром та автокореляційною функцією процесу існує однозначний зв’язок, що описується парою перетворень Фур’є:
Ширину енергетичного спектра Δω визначають як:
Енергетичний спектр є парною функцією свого аргументу. При використанні одностороннього енергетичного спектра поняття негативних частот зникає. Розглянемо далі необхідні нам основи електромагнітного поля.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 (2.1)
(2.1) , і синусоїдальним
, і синусоїдальним  сигналами, тобто
сигналами, тобто (2.2)
(2.2)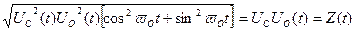 . (2.3)
. (2.3)




 дорівнює його амплітуді, тобто
дорівнює його амплітуді, тобто . (2.4)
. (2.4) , (2.5)
, (2.5) – поточні значення амплітуд імпульсів.
– поточні значення амплітуд імпульсів. . (2.6)
. (2.6)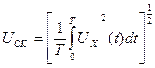 , (2.7)
, (2.7) – значення рівня шумів на інтервалі вимірювання.
– значення рівня шумів на інтервалі вимірювання. . (2.8)
. (2.8)

 . (2.9)
. (2.9) , (2.10)
, (2.10)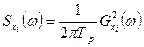
 . (2.11)
. (2.11) , (2.12)
, (2.12)
 . (2.13)
. (2.13) ;
;  (квадрат дисперсії процесу Х);
(квадрат дисперсії процесу Х);  (парність функції).
(парність функції). (2.14)
(2.14) ,
, . (2.15)
. (2.15) . (2.16)
. (2.16)


