
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базові відомості щодо електромагнітного поля та ПЕМВНСодержание книги
Поиск на нашем сайте
Основні закономірності електромагнітного поля описуються системою рівнянь Максвела, які у диференціальній формі можна представити так [16].
де H – вектор напруженості магнітного поля; E – вектор напруженості електричного поля; rot – вихор. Смисл ротора – це швидкість змінення напряму вектора поля у просторі;
μ 0 = 4π∙10-7 (Гн/м) – магнітна постійна вакууму; ρ – об’ємна щільність електричного заряду, причому σ – питома провідність, яка пов’язана з питомим опором провідників ε 2– діелектрична проникність середовища; μ 2 – магнітна проникність середовища. Поняття «дивергенція» перекладається українською мовою як розбіжність або збіжність ліній векторного поля. В однорідному векторному полі дивергенція дорівнює нулю. Фізичний смисл дивергенції у будь-якій точці поля – це швидкість зміни вектора у своєму напрямі (зміни модуля вектора) [17]. Побічні електромагнітні випромінювання та наведення (ПЕМВН) можна поділити на [18, с. 129; див. 10, с. 378]: – не передбачені у роботі технічних засобів акустоелектричні перетворення; – паразитні зв’язки та наведення; – побічні низькочастотні випромінювання; – побічні високочастотні випромінювання. Під низькочастотними випромінюваннями розуміють електромагнітні випромінювання з частотами чутного звукового діапазону. Джерелами таких випромінювань є пристрої та ланцюги, випадкові та не випадкові акустоелектричні перетворювачі зі з’єднувальними лініями. До високочастотних небезпечних випромінювань відносяться електромагнітні випромінювання від високочастотних ланцюгів, якими циркулює секретна або конфіденційна інформація. Джерелом таких випромінювань можуть бути: – підсилювачі та логічні елементи у режимі паразитної генерації; – генератори підмагнічування та стирання магнітофонів; – гетеродини радіо- та телевізійних приймачів; – елементи ВЧ - нав’язування; – пристрої та вузли комп’ютерної техніки. Сигнали можна представляти функціями часу або у вигляді частотних спектрів. При дослідженні ПЕМВН сигнали зазвичай представляються у вигляді частотних спектрів.
Якщо сигнал визначається гармонічною функцією A cos(ωt + ψ), то на шкалі частот вона визначається заданою амплітудою А та початковою фазою ψ (рис. 2.4).
Рисунок 2.4 – Звичне спектральне представлення гармоніки: гармонічна частота на шкалі частот та на шкалі фази
За комплексної форми запису косинусоїди
вводиться чисто математичне поняття негативної кутової частоти, а шкала частот доповнюється негативною напіввіссю. Амплітудний і фазовий спектр у цьому випадку зображаються парами ординат (рис. 2.5), що відповідають позитивним та негативним значенням кутової частоти.
Рисунок 2.5 – Спектральне представлення гармоніки для комплексної форми запису косинусоїди
Не синусоїдальні сигнали можуть бути розкладені у ряд Фур’є, тобто представлені у вигляді дискретного ряду гармонік. Для тригонометричної форми запису ряду Фур’є для функції
амплітуди An і початкові фази ψn визначаються формулами
де n – номер гармоніки. В (2.20) коефіцієнти розкладання
де Т – період основної частоти, ω 1 = 2π T – основна частота. Для комплексної форми запису ряду Фур’є
комплексні амплітуди визначаються за формулою
в якій An, ψn, an, bn обчислюються за раніше наведеними формулами. Сукупність амплітуд відповідних гармонік Лінійчастий фазовий спектр утворюють аргументи (фази) комплексних коефіцієнтів ряду Фур’є. Розглянемо періодичну послідовність прямокутних імпульсів з періодом повторення, що значно перевищує тривалість імпульсу (рис. 2.6, а) та характерне для засобів цифрової обробки інформації. Характеристикою послідовності імпульсів є щілинність N = T/ t 1. Імпульсу на осі ординат (рис. 2.6, а) відповідає часова функція
Згідно з (2.23) вираз для комплексних амплітуд визначається як
На підставі (2.25) можна побудувати спектр. Якщо в останньому виразі позначити
Число спектральних ліній між початком відліку за шкалою частот (або номерів гармонік) та першим нулем обвідної дорівнює числу спектральних ліній між сусідніми нулями та складає N – 1. Положення нулів обвідної спектра на осі частот не залежить від періоду Т, а визначається лише тривалістю імпульсу. При цьому коефіцієнти ряду заданого періодичного сигналу обернено пропорційні періоду (або щілинності імпульсів). Зі зростанням Т обвідна знижується, прагнучи при Т > ∞ збігтися з віссю абсцис.
Рисунок 2.6 – Послідовність прямокутних імпульсів (а) та її спектр (б)
Перепишемо часову функцію
Тут
У міру зростання періоду Т інтервал Інтеграл під знаком суми при У реальних умовах існує лише суцільний спектр імпульсів. Амплітуди гармонічних складових для послідовності імпульсів значно більші, ніж амплітуда обвідної спектральної густини для одиничного імпульсу. Проте нормами визначено розрахунок захищеності по одному імпульсу незалежно від попередніх і подальших. Тому у розрахункових формулах введена операція ділення на корінь квадратний із частоти проходження імпульсів, а невірне визначення цієї частоти приводить до помилкового результату.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.129.162 (0.007 с.) |

 (2.17)
(2.17) (Ф/м) – електростатична постійна вакууму, вона визначає швидкість поширення хвиль у вакуумі;
(Ф/м) – електростатична постійна вакууму, вона визначає швидкість поширення хвиль у вакуумі; Ом. Також має місце наступне відношення компонент поля нормованих шумів (атмосферних завад)
Ом. Також має місце наступне відношення компонент поля нормованих шумів (атмосферних завад)  Ом;
Ом;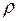 формулою
формулою  ;
;
 . (2.18)
. (2.18)
 (2.19)
(2.19) ;
;  , (2.20)
, (2.20) ;
;  , (2.21)
, (2.21) (2.22)
(2.22) , (2.23)
, (2.23)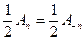 (модулів комплексних коефіцієнтів ряду Фур’є, відкладених проти відповідних позитивних і негативних частот) являє симетричний щодо осі ординат лінійчастий амплітудний спектр.
(модулів комплексних коефіцієнтів ряду Фур’є, відкладених проти відповідних позитивних і негативних частот) являє симетричний щодо осі ординат лінійчастий амплітудний спектр.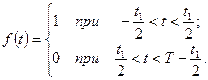 (2.24)
(2.24) . (2.25)
. (2.25) , то очевидно, що обвідна спектра, показана на рис. 2.6, б, описується простим виразом
, то очевидно, що обвідна спектра, показана на рис. 2.6, б, описується простим виразом  .
.
 у наступному вигляді
у наступному вигляді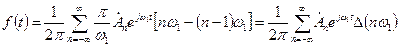 . (2.26)
. (2.26) – частотний інтервал між складовими ряду Фур’є. Оскільки
– частотний інтервал між складовими ряду Фур’є. Оскільки  , то
, то . (2.27)
. (2.27) скорочується, а лінійчастий спектр все більш згущується за умови зменшення модулів An комплексних амплітуд. При
скорочується, а лінійчастий спектр все більш згущується за умови зменшення модулів An комплексних амплітуд. При 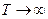 дискретні частоти
дискретні частоти 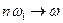 , тобто спектр із дискретного перетворюється у суцільний, а
, тобто спектр із дискретного перетворюється у суцільний, а  .
. .
.


