
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование периодических сигналовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Кафедра радиотехники и МДС
Анализ сигналов и систем
Пояснительная записка к курсовой работе на тему: «ИССЛЕДОВАНИЕ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ»
Работу выполнила: Панина Ж.С., группа 537 Работу проверил: Воронов К.Е.
Оценка: Дата:
Самара 2009 г.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
СОДЕРЖАНИЕ Введение………………………………………………………………………………………..5 1 Аппроксимация сигнала…………………………………………………...8 2 Исследование спектральных характеристик сигнала…………………..13 2.1 Построение АЧХ и ФЧХ периодического сигнала…………………13 2.2 Построение АЧХ и ФЧХ непериодического сигнала………………22 2.3 Средняя энергия и средняя мощность периодического сигнала…..24 2.4 Энергия в спектре непериодического сигнала……………………...26 2.5 Некоторые свойства преобразований Фурье………………………..27 2.5.1 Сдвиг сигнала во времени……………………………………...27 2.5.2 Изменение масштаба времени…………………………………28 2.5.3 Дифференцирование и интегрирование сигнала……………..30 2.5.4 Сложение с прямоугольным импульсом……………………...32 2.5.5 Расщепление сигнала…………………………………………...33 3 Анализ сигнала с применением программного пакета OrCAD 10.5…..35 3.1 Моделирование сигнала в пакете OrCAD …………………………..35 3.2 Ограничение спектра сигнала ……………………………………….37 3.3 Исследование сигнала с введёнными помехами………………………………………………………………39 3.4 Восстановление сигнала по его спектру…………………………….45 3.5 Фильтрация сигнала…………………………………………………..47 3.5.1 Фильтрация НЧ помехи …………………………………...…...49 3.5.2 Фильтрация ВЧ помехи…………………………..…………….51 3.5.3 Фильтрация совместного действия НЧ и ВЧ помехи………...53 4 Исследование прохождения сигнала через НЭ…………………………55 4.1 Аппроксимация степенным полиномом…………………………….55 4.2 Кусочно-линейная аппроксимация…………………………………..62 4.3 Бигармоническое воздействие……………………………………….68 4.4 Моделирование прохождения сигналов через НЭ в пакете OrCAD72 5 Расчёт сигнала на выходе цепи с использованием метода интеграла Дюамеля………………………………………………………………………….76
Заключение……………………………………………………………………….82 Список используемых источников……………………………………………..83 Приложение………………………………………………………………………84 РЕФЕРАТ
Пояснительная записка: АНАЛИЗ СИГНАЛОВ, ЭНЦЕФАЛОЛОГРАММЫ, ПРЕОБРАЗОВАНИЕ СИГНАЛОВ, ФИЛЬТРАЦИЯ ПОМЕХ, НЕЛИНЕЙНЫЙ ЭЛЕМИЕНТ
Объектом исследования является энцефолограмма. Цель работы: закрепить изученные ранее методы анализа сигналов, изменений, связанных с прохождением сигнала через нелинейные цепи. Исследовать способы выделения полезной информации из сигнала с шумами.
В результате работы проведён многогранный анализ представленной энцефалограммы, проведена фильтрация шумов, наложенных на информационный сигнал. Проведён анализ сигнала, прошедшего через заданный нелинейный элемент.
.
ВВЕДЕНИЕ
В данной курсовой работе должны быть закреплены изученные методы анализа сигналов, изменения связанные с прохождением сигналов через нелинейные цепи, исследованы способы решения практической задачи - выделения полезной информации, содержащейся в сигнале, на фоне помех, получены навыки моделирования реальных медицинских сигналов в пакете программ ORCAD.
Задание на курсовую работу по предмету Анализ сигналов и систем «Исследование энцефолограммы»
Задан сигнал – элемент энцефолограммы №39
Элемент энцефолограммы
Параметры сигнала и воздействующих помех приведены в таблице 1.
Таблица 1 - Параметры сигнала и воздействующих помех
Параметры ВАХ нелинейного элемента приведены в таблице 2.
Таблица 2 - Параметры ВАХ нелинейного элемента
Параметры гармонического сигнала описаны в таблице 3.
Таблица 3 - Параметры гармонического сигнала
Параметры входного сигнала для случая кусочно-линейной аппроксимации НЭ приведены в таблице 4.
Таблица 4 - Параметры входного сигнала для случая кусочно-линейной аппроксимации НЭ
Схема №14
Аппроксимация сигналов
Медицинские сигналы имеют достаточно сложную форму. Для того, чтобы иметь возможность применить к исследованию данного сигнала математические методы, необходимо аппроксимировать его математической функцией, удобной для дальнейшего анализа и в то же время с достаточной точностью передающей форму сигнала. Наиболее простым методом преобразования является метод графической аппроксимации. Функция разбивается на несколько участков с различным характером зависимости напряжения от времени. Выбираются участки по описанию близкие к линейным, гармоническим и полиномиальным функциям. Так как сигнал является периодическим, то его следует рассматривать на временном интервале, равном периоду сигнала. После разбиения интервала, на котором представлен сигнал, на характерные участки, определяем координаты точек соединяющих участки и координаты точек на концах интервала аппроксимации. Например аппроксимирующую функцию построим из совокупности степенных функций 1-й и 2-й степени. Графики таких функций являются прямые и параболы соответственно. Для каждого участка составим уравнения прямой (или параболы), проходящей через точки – границы участка (причем, если линия является параболой, то необходимо задать координаты еще одной какой-либо точки, т.к. уравнение параболы однозначно определяется по трем точкам). Данный метод сразу позволяет получить непрерывную аппроксимирующую функцию. Уравнение прямой имеет вид y(x)=kx+b. Пусть заданы координаты двух точек (x1,y1) и (x2,у2), через которые проходит данная прямая, тогда коэффициенты k и b определятся по формулам
Уравнение параболы имеет вид у(х) = ах2 + hx + с. Пусть заданы координаты трех точек (х1у1,), (x2,у2) и (х3,у3), через которые проходит данная парабола, тогда коэффициенты а, b и с определятся по формулам:
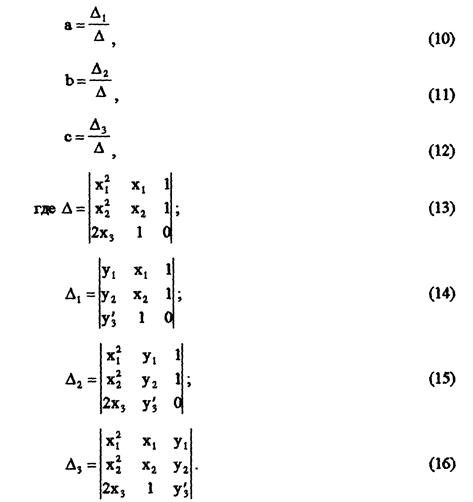
Более того, в случае сопряжения параболы на какой-либо из границ участка с прямой из соседнего участка, возможно получение уравнения параболы по двум известным точкам на границе интервала и известному угловому коэффициенту прямой, с которой сопрягается парабола. В таком случае аппроксимирующая функция в месте сопряжения двух линий, составляющих ее, является не только непрерывной, но и гладкой (то есть не имеющей изломов, что и наблюдается в природе). Пусть заданы координаты двух точек (х1,y1) и (х2,у2), через которые проходит данная парабола, и значение производной в какой либо точке (хз,у3), тогда коэффициенты а, b и с определятся по формулам (10)-(16). Определив точки сопряжения линий и воспользовавшись формулами (1-16), получим выражение для аппроксимирующей функции.
Сигнал № 37. Параметры сигнала: Табица№1: №14
. Рисунок 1 – Заданная энцефолограмма
Выделив 8 участков аппроксимации, определим аналитические уравнения каждого из участков.
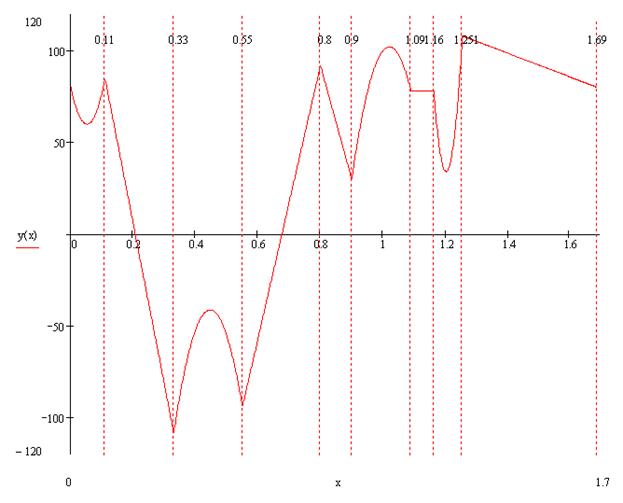
Вид аппроксимированного сигнала представлен на рис.2
Рисунок 2 – Аппроксимированный сигнал Периодического сигнала Пусть сигнал s(t) (ток, напряжение) представляет собой сложную периодическую функцию времени с периодом Т. Энергия такого сигнала, длящегося от t=-∞ до t=∞, бесконечно велика. Основной интерес представляет средняя мощность периодического сигнала и распределение этой мощности между отдельными гармониками сигнала. Очевидно, что средняя мощность сигнала, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Таким образом, средняя мощность периодического сигнала
При использовании тригонометрической формы ряда Фурье, учитывая, что С0=а0/2,
Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя):
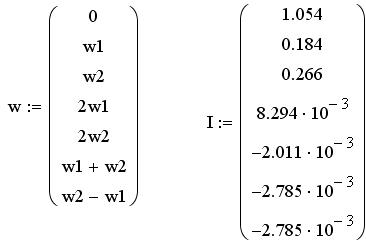
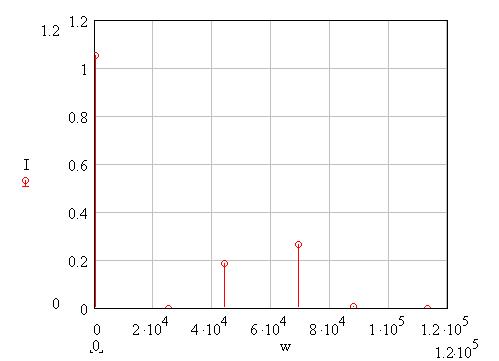
Символом I0=а0/2 обозначена постоянная составляющая, а In =An – амплитудой n-ой гармоники тока.
Итак, средняя мощность периодической последовательности равна сумме средних мощностей всех составляющих в спектре и не зависит от начальных фаз отдельных составляющих. Для данного сигнала средняя мощность равна:
Энергия периодического сигнала:
Проверка размерности величин:
Мы берём амплитуду в мВ, возводим в квадрат, получаем мкВ.
Сдвиг сигнала во времени Пусть сигнал s1(t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1(ω). При задержке этого сигнала на время t0 получим новою функцию времени s(t2)=s(t – t0), существующую на интервале от t1+t0 до t2+t0. Спектральная плотность сигнала s2(t) равна
Из этого соотношения видно, что сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси не зависит.
Сдвиг сигнала во времени осуществляется на величину 0.1Т = 0,169с
Рисунок 7 – ФЧХ исходного (Q(w)) и задержанного (Q1(w)) сигналов
Вывод: Сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси времени не зависит.
Изменение масштаба времени Пусть сигнал s1(t) подвергается сжатию во времени. Новый сжатый сигнал s2(t) связан с исходным соотношением s2(t)=s1(nt), n>1. Спектральная плотность сжатого импульса
Рисунок 8 – АЧХ исходного(S(w)) и сжатого S1(w) сигналов
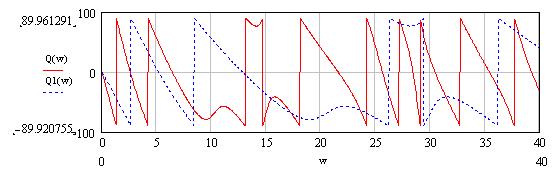
Рисунок 9 – ФЧХ исходного(S(w)) и сжатого S1(w) сигналов
Вывод: При сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшится в n раз.
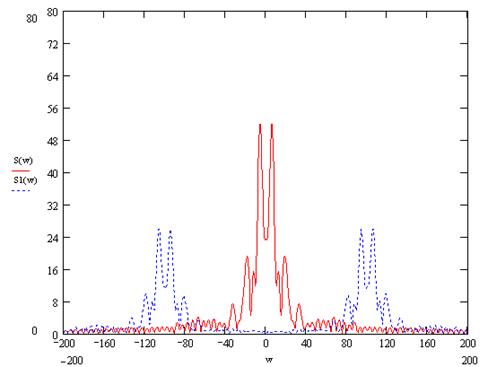
Расщепление сигнала Возьмём ω0= 100
Рисунок 15 – АЧХ исходного (S(w)) и расщепленного (S1(w)) сигналов
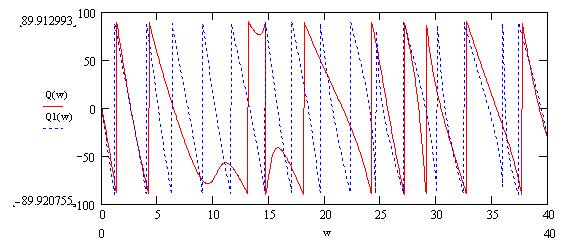
Рисунок 16 – ФЧХ исходного (S(w)) и расщепленного (S1(w)) сигналов Между сигналом
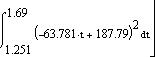
Ограничение спектра сигнала Определим полосу частот, занимаемую сигналом по уровню 0,9, т.е. полосу частот, на которой укладывается 90% площади фигуры, ограниченной спектром и осями координат. Составим схему в пакете OrCad для ограничения спектра сигнала по уровню 0,9 с помощью идеального фильтра LOPASS, частота среза которого равна наибольшему значению полосы частот ωс, занимаемой сигналом по уровню 0,9. В программе PSpice ограничение спектра исследуемого сигнала реализуется путем применения фильтра нижних частот с П - образной АЧХ, определяемой тремя числами - (частота, АЧХ в дБ, фаза в градусах). Для определения максимальной частоты спектра, занимаемой сигналом воспользуемся равенством Парсеваля:
С помощью данного соотношения найдём энергию заданного сигнала.
Е=9289мкДж
Теперь определим максимальную частоту спектра при уровне 0.9Е. 90% энергии лежит в первых трёх гармониках. Приведём расчёт:
Тогда граничная F полосы, в которой лежит 90% сигнала будет равна F=2*(1/Т), где 2- номер гармоники. (нулевую гармонику мы не берём, т.к. у неё нулевая частота).
Т= 1,69 F=2*(1/Т)=1,18 Гц
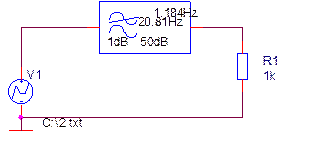
Для проведения расчёта в пакете программ OrCAD 10.5 соберём схему, указанную на рисунке 21.
Рисунок 21 – Схема, реализующая ограничения сигнала по уровню 90% его первоначальной энергии.
Рисунок 22 – Исходный V(LOPASS:IN) и ограниченный V(R1:2) сигналы
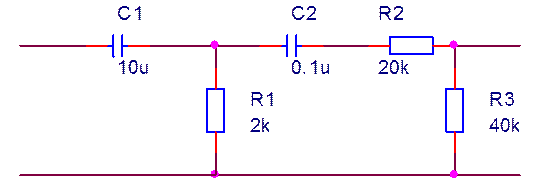
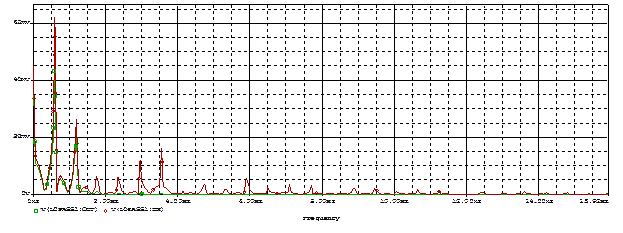
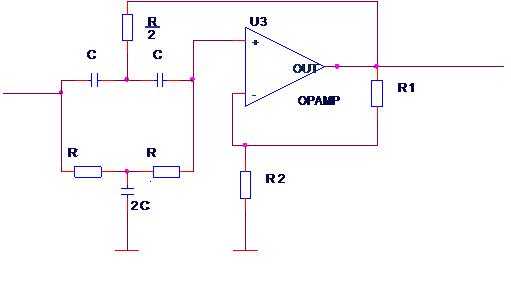
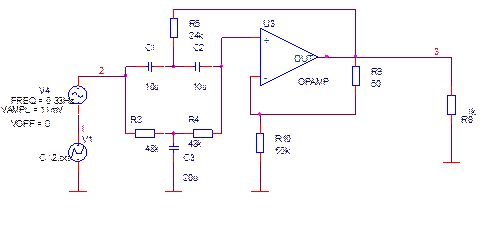
Рисунок 23 – АЧХ спектра исходный V(LOPASS1:IN) и ограниченный V(R1:2) сигнала Фильтрация сигнала Тот факт, что помехи искажают сигнал и вызывают ложную информацию, заставляет искать пути их ликвидации или уменьшения. С этой целью обычно применяются различные фильтры. Активные фильтры представляют собой комбинацию пассивных частотно избирательных цепей и активных элементов - как правило сложных транзисторных устройств, которые передают в пассивные цепи некоторую мощность от источника питания. Широкое применение нашли активные RC - фильтры, где в качестве активного элемента используется ОУ, в качестве пассивных RC - цепей. Так как на заданный полезный сигнал действуют одногармоническая НЧ и ВЧ помеха, с известными частотами, то целесообразно использовать заграждающий фильтр. Данный выбор фильтра позволит подавить помехи с наименьшими искажениями полезного сигнала. В данной курсовой работе рассматривается активный заграждающий фильтр второго порядка с двойным Т-образным мостом (рис41).
Рисунок 41 - Активный заграждающий фильтр второго порядка с двойным Т-образным мостом
Двойной Т-образный мост представляет собой пассивный заграждающий RC-фильтр. Его добротность Q составляет 0,25. Ее можно повысить, если двойной Т-образный мост включить в контур обратной связи усилителя. Сигналы высоких и низких частот проходят через двойной Т-образный фильтр без изменения. Для них выходное напряжение преобразователя полного сопротивления равно k* U e. На резонансной частоте выходное напряжение равно нулю. В этом случае двойной Т-образный фильтр эквивалентен заземленному резистору R/2. При этом резонансная частота fr = 1/2πRC не изменяется. Передаточная функция схемы на рис. 36 имеет вид
С помощью этого выражения можно непосредственно определять требуемые параметры фильтра. Задав коэффициент усиления повторителя напряжения равным 1, получим Q = 0,5. При увеличении коэффициента усиления добротность Q →∞ приk→2 Условием правильной работы схемы является оптимальная установка резонансной частоты и коэффициента передачи двойного Т-образного фильтра. Настройка схемы, особенно при больших значениях добротности, достаточно сложна. Это связано с тем, что изменение сопротивления одновременно влияет на оба параметра. В этом смысле предпочтительнее использовать активный заграждающий фильтр с мостом Вина-Робинсона.
Расчёт элементов фильтра: Ёмкость С задаётся произвольно в микрофарадах. R=1/2πCfr, где fr – частота среза фильтра, берётся равной частоте входной помехи. (Частота среза - это частота, на которой уровень подавляемого сигнала становится на 3 дБ меньше, чем уровень пропускаемого сигнала.) Для НЧ помехи fr= 0,33 Гн Для ВЧ помехи fr= 8 Гн Резисторы R1 и R2 задают коэффициент усиления схемы. k=R1/R2
Фильтрация НЧ помех Рассчитаем элементы схемы для фильтрации НЧ помехи
Смоделируем данную работу данной схемы в пакете OrCAD
Рисунок 42– Схема подавления НЧ помехи
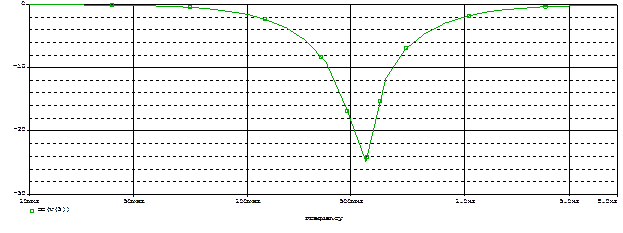
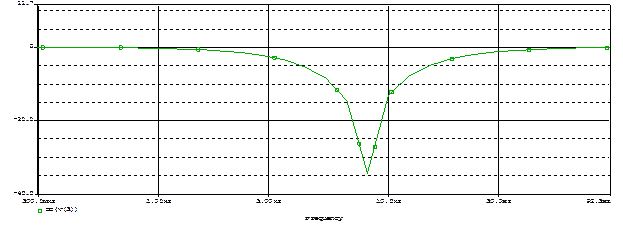
Рисунок 43 – АЧХ фильтра
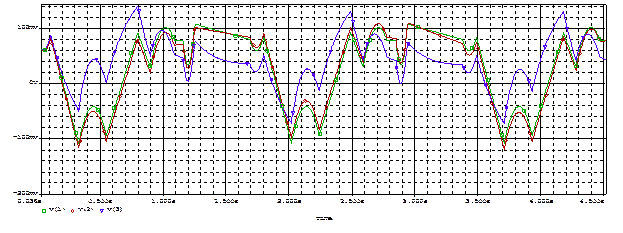
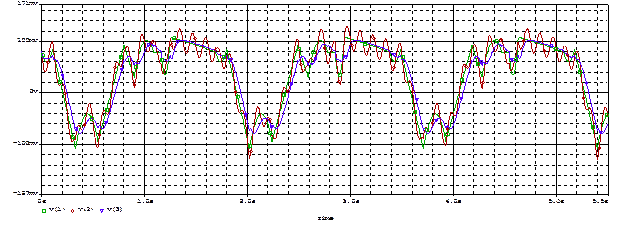
Рисунок 44 – График исходного (V(1)), искажённого НЧ помехой (V(2)) и отфильтрованного сигнала (V(3))
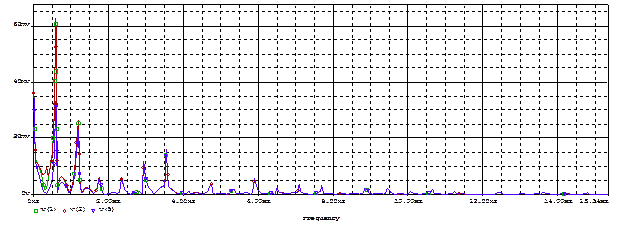
Рисунок 45 – График АЧХ спектра исходного (V(1)), искажённого НЧ помехой (V(2)) и отфильтрованного сигнала (V(3))
Фильтрация ВЧ помех Рассчитаем элементы схемы для фильтрации НЧ помехи
Смоделируем данную работу данной схемы в пакете OrCAD
Рисунок 46 – Схема подавления ВЧ помехи
Рисунок 47 – АЧХ фильтра
Рисунок 48 – График исходного (V(1)), искажённого ВЧ помехой (V(2)) и отфильтрованного сигнала (V(3))
Рисунок 49 – График АЧХ спектра исходного (V(1)), искажённого ВЧ помехой (V(2)) и отфильтрованного сигнала (V(3))
Бигармоническое воздействие На НЭ воздействуют два гармонических сигнала:
Параметры сигналов: A1=0.11В, f1=7кГц, U0=1,5В А2=0,15В, f2=11кГц, U0=0В
Этот бигармонический сигнал поступает на нелинейный элемент, у которого ВАХ описывается выражением:
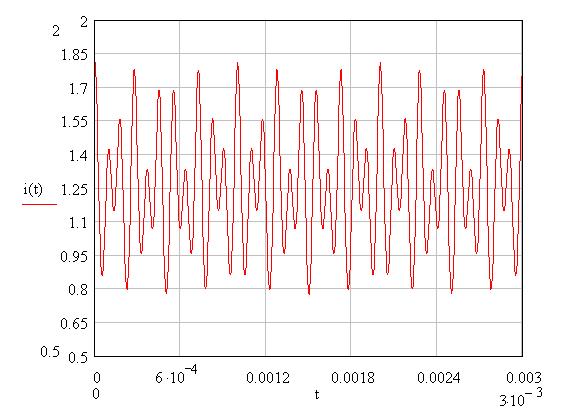
Рисунок 65 – Бигармонический сигнал на входе НЭ
Рисунок 66 – Спектр сигнала на входе НЭ
Для упрощения рассмотрим слабо нелинейный режим, то есть когда достаточно учитывать только линейный и квадратичный члены полинома.
Получим
На выходе появляются дополнительные составляющие на кратных, комбинационных частотах, которые можно посчитать по формулам:
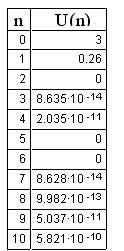
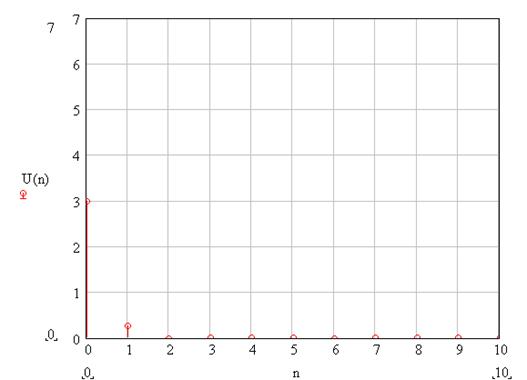
Рисунок 67 – Спектр бигармонического сигнала на выходе НЭ
ЗАКЛЮЧЕНИЕ В ходе выполнения данной курсовой работы были закреплены изученные ранее методы анализа сигналов, изменения связанные с прохождением сигналов через нелинейные цепи, исследованы способы решения практической задачи – выделения полезной информации, содержащейся в сигнале, на фоне помех.
Приложение
СПИСОК СОКРАЩЕНИЙ
АЧХ – амплитудно-частотная характеристика ВАХ – вольт-амперная характеристика НЭ – нелинейный элемент ФЧХ – фазо-частотная характеристика
Кафедра радиотехники и МДС
Анализ сигналов и систем
Пояснительная записка к курсовой работе на тему: «ИССЛЕДОВАНИЕ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ»
Работу выполнила: Панина Ж.С., группа 537 Работу проверил: Воронов К.Е.
Оценка: Дата:
Самара 2009 г.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
СОДЕРЖАНИЕ Введение………………………………………………………………………………………..5 1 Аппроксимация сигнала…………………………………………………...8 2 Исследование спектральных характеристик сигнала…………………..13 2.1 Построение АЧХ и ФЧХ периодического сигнала…………………13 2.2 Построение АЧХ и ФЧХ непериодического сигнала………………22 2.3 Средняя энергия и средняя мощность периодического сигнала…..24 2.4 Энергия в спектре непериодического сигнала……………………...26 2.5 Некоторые свойства преобразований Фурье………………………..27 2.5.1 Сдвиг сигнала во времени……………………………………...27 2.5.2 Изменение масштаба времени…………………………………28 2.5.3 Дифференцирование и интегрирование сигнала……………..30 2.5.4 Сложение с прямоугольным импульсом……………………...32 2.5.5 Расщепление сигнала…………………………………………...33 3 Анализ сигнала с применением программного пакета OrCAD 10.5…..35 3.1 Моделирование сигнала в пакете OrCAD …………………………..35 3.2 Ограничение спектра сигнала ……………………………………….37 3.3 Исследование сигнала с введёнными помехами………………………………………………………………39 3.4 Восстановление сигнала по его спектру…………………………….45 3.5 Фильтрация сигнала…………………………………………………..47 3.5.1 Фильтрация НЧ помехи …………………………………...…...49 3.5.2 Фильтрация ВЧ помехи…………………………..…………….51 3.5.3 Фильтрация совместного действия НЧ и ВЧ помехи………...53 4 Исследование прохождения сигнала через НЭ…………………………55 4.1 Аппроксимация степенным полиномом…………………………….55 4.2 Кусочно-линейная аппроксимация…………………………………..62 4.3 Бигармоническое воздействие……………………………………….68 4.4 Моделирование прохождения сигналов через НЭ в пакете OrCAD72 5 Расчёт сигнала на выходе цепи с использованием метода интеграла Дюамеля………………………………………………………………………….76
Заключение……………………………………………………………………….82 Список используемых источников……………………………………………..83 Приложение………………………………………………………………………84 РЕФЕРАТ
Пояснительная записка: АНАЛИЗ СИГНАЛОВ, ЭНЦЕФАЛОЛОГРАММЫ, ПРЕОБРАЗОВАНИЕ СИГНАЛОВ, ФИЛЬТРАЦИЯ ПОМЕХ, НЕЛИНЕЙНЫЙ ЭЛЕМИЕНТ
Объектом исследования является энцефолограмма. Цель работы: закрепить изученные ранее методы анализа сигналов, изменений, связанных с прохождением сигнала через нелинейные цепи. Исследовать способы выделения полезной информации из сигнала с шумами.
В результате работы проведён многогранный анализ представленной энцефалограммы, проведена фильтрация шумов, наложенных на информационный сигнал. Проведён анализ сигнала, прошедшего через заданный нелинейный элемент.
.
ВВЕДЕНИЕ
В данной курсовой работе должны быть закреплены изученные методы анализа сигналов, изменения связанные с прохождением сигналов через нелинейные цепи, исследованы способы решения практической задачи - выделения полезной информации, содержащейся в сигнале, на фоне помех, получены навыки моделирования реальных медицинских сигналов в пакете программ ORCAD.
Задание на курсовую работу по предмету Анализ сигналов и систем «Исследование энцефолограммы»
Задан сигнал – элемент энцефолограммы №39
Элемент энцефолограммы
Параметры сигнала и воздействующих помех приведены в таблице 1.
Таблица 1 - Параметры сигнала и воздействующих помех
Параметры ВАХ нелинейного элемента приведены в таблице 2.
Таблица 2 - Параметры ВАХ нелинейного элемента
Параметры гармонического сигнала описаны в таблице 3.
Таблица 3 - Параметры гармонического сигнала
Параметры входного сигнала для случая кусочно-линейной аппроксимации НЭ приведены в таблице 4.
Таблица 4 - Параметры входного сигнала для случая кусочно-линейной аппроксимации НЭ
Схема №14
ИССЛЕДОВАНИЕ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Периодическим называется любой сигнал, для которого выполняется условие Аппроксимация сигналов
Медицинские сигналы имеют достаточно сложную форму. Для того, чтобы иметь возможность применить к исследованию данного сигнала математические методы, необходимо аппроксимировать его математической функцией, удобной для дальнейшего анализа и в то же время с достаточной точностью передающей форму сигнала. Наиболее простым методом преобразования является метод графической аппроксимации. Функция разбивается на несколько участков с различным характером зависимости напряжения от времени. Выбираются участки по описанию близкие к линейным, гармоническим и полиномиальным функциям. Так как сигнал является периодическим, то его следует рассматривать на временном интервале, равном периоду сигнала. После разбиения интервала, на котором представлен сигнал, на характерные участки, определяем координаты точек соединяющих участки и координаты точек на концах интервала аппроксимации. Например аппроксимирующую функцию построим из совокупности степенных функций 1-й и 2-й степени. Графики таких функций являются прямые и параболы соответственно. Для каждого участка составим уравнения прямой (или параболы), проходящей через точки – границы участка (причем, если линия является параболой, то необходимо задать координаты еще одной какой-либо точки, т.к. уравнение параболы однозначно определяется по трем точкам). Данный метод сразу позволяет получить непрерывную аппроксимирующую функцию. Уравнение прямой имеет вид y(x)=kx+b. Пусть заданы координаты двух точек (x1,y1) и (x2,у2), через которые проходит данная прямая, тогда коэффициенты k и b определятся по формулам
Уравнение параболы имеет вид у(х) = ах2 + hx + с. Пусть заданы координаты трех точек (х1у1,), (x2,у2) и (х3,у3), через которые проходит данная парабола, тогда коэффициенты а, b и с определятся по формулам:
Более того, в случае сопряжения параболы на какой-либо из границ участка с прямой из соседнего участка, возможно получение уравнения параболы по двум известным точкам на границе интервала и известному угловому коэффициенту прямой, с которой сопрягается парабола. В таком случае аппроксимирующая функция в месте сопряжения двух линий, составляющих ее, является не только непрерывной, но и гладкой (то есть не имеющей изломов, что и наблюдается в природе). Пусть заданы координаты двух точек (х1,y1) и (х2,у2), через которые проходит данная парабола, и значение производной в какой либо точке (хз,у3), тогда коэффициенты а, b и с определятся по формулам (10)-(16). Опр
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.105 (0.01 с.) |








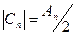 получаем
получаем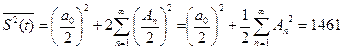 мВт
мВт

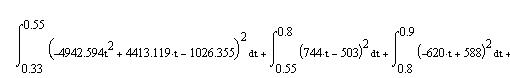


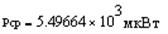

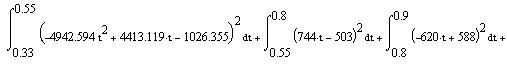

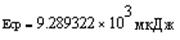
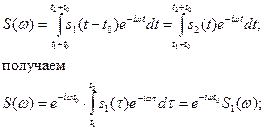

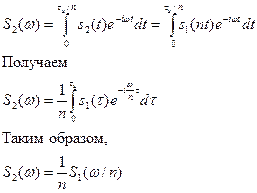 n= 2
n= 2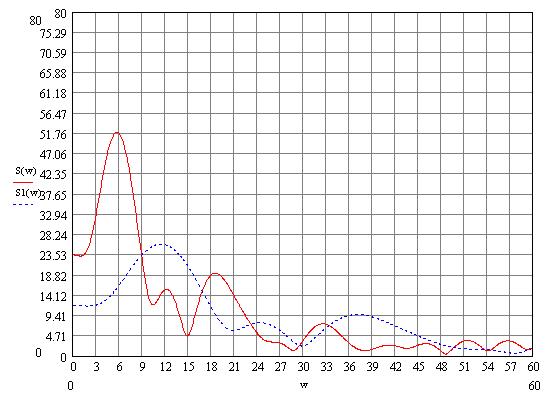
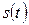 и его спектром
и его спектром 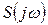 существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из возможных преобразований сигнала рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг сигнала во времени, изменение масштаба времени, дифференцирование и интегрирование сигнала, сложение и произведение сигналов.
существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из возможных преобразований сигнала рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг сигнала во времени, изменение масштаба времени, дифференцирование и интегрирование сигнала, сложение и произведение сигналов.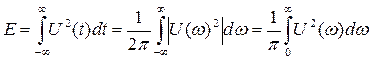
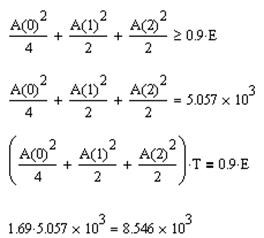

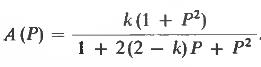




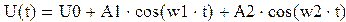
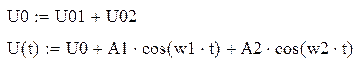
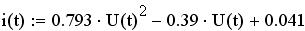
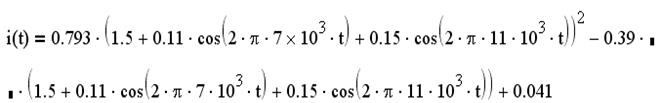
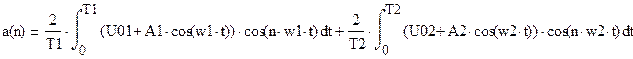
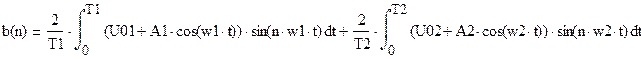
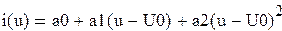
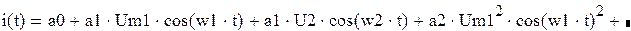
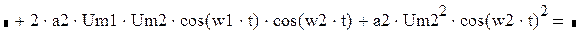


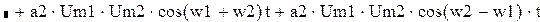

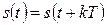 , где «период» Т является конечным отрезком, а k – любое целое число.
, где «период» Т является конечным отрезком, а k – любое целое число.


