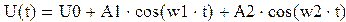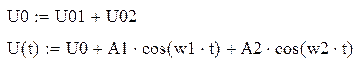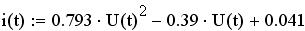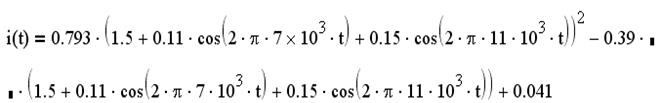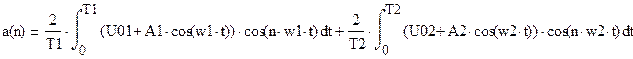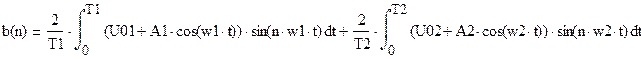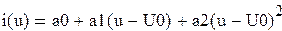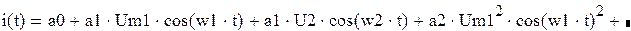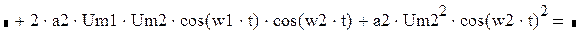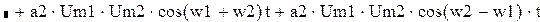Фильтрация совместного действия НЧ и ВЧ помехи

Реализацию подавления НЧ и ВЧ помех осуществим последовательным соединением НЧ и ВЧ фильтра (рис.45).

Рисунок 50 – Схема подавления ВЧ и НЧ помех

Рисунок 51 – АЧХ фильтра

Рисунок 52 – График исходного (V(1)), искажённого помехами (V(2)) и отфильтрованного сигнала (V(3))

Рисунок 53 – График АЧХ спектра исходного (V(1)), искажённого ВЧ помехой (V(2)) и отфильтрованного сигнала (V(3))

 

ВЫВОД:

Применяя активный заграждающий фильтр второго порядка с двойным Т-образным мостом для фильтрации НЧ, ВЧ и совместного действия помех, при настройке частоты среза фильтра на частоту помехи, мы добились почти полного её подавления. При использовании данных фильтров происходит фильтрация помехи и незначительная фильтрация полезного сигнала в окрестности частоты помехи, это связано с добротностью контуров, а в целом полезный сигнал сохраняется.

Исследование прохождения сигнала через НЭ

Аппроксимация степенным полиномом

Этот способ аппроксимации основан на разложении нелинейной ВАХ в ряд Тейлора в окрестности рабочей точки „u₀”

В зависимости от амплитуды входного воздействия, формы ВАХ, положения рабочей точки „u₀” на ВАХ степенной полином часто удаётся упростить, используя для описания несколько членов ряда.

По данным таблицы 2 подбираем выражение для ВАХ: в 1-ом случае это парабола. Находим уравнение параболы по 3-м точкам с координатами (1; 0.2), (1.5; 0.85), (2; 2,2) выбор такого количества точек обусловлен тем, что работаем с НЭ, у которого малые по амплитуде сигналы.

Получим график I(U) – зависимость тока от напряжения на выходе НЭ.

Таблица 2 – ВАХ НЭ

I,A	U,B
0.16	0.5
0.36
1.2	1.5
2.5
	2.5

 

I(U)=0,7929*U²-0,3901*U+0,0407

 

Рисунок 54 – ВАХ нелинейного элемента

 

Таблица 3 – Аппроксимированная ВАХ НЭ

I,A	U,B
0,0407
0.4435
2.4321

 

Рисунок 55 – Степенная аппроксимация ВАХ НЭ (I(U)) и исходная ВАХ НЭ (Itabl(U))

 

Построим сигнал на входе нелинейного элемента. Параметры сигнала: A=0.11B, U0=1.5B, f=7кГц, w=2∙π∙f

Рисунок 56 – Сигнал на входе НЭ

Рассчитаем и построим спектр выходного напряжения:

с

 

 

 

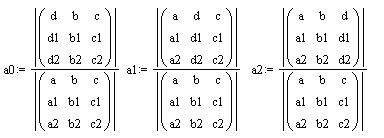
Рисунок 57 – Спектр гармонического сигнала

Получаем спектр из двух гармоник, первая – нулевая (за счет постоянной составляющей сигнала), вторая – на частоте ω, т.е. на частоте входного сигнала.

При прохождении через нелинейный элемент напряжение преобразуется в выходной ток. Найдем гармоники данного выходного сигнала. Для этого представим i(u) как: i(u)=a0+a1(u-U0)+a2(u-U0)²+…, где коэффициенты a0,a1,a2 … - некоторые числа.

Для нахождения коэффициентов a0,a1,a2 нужно решить систему уравнений:

Решим систему уравнений матричным способом. Представим систему уравнений в матричном виде:

(А)*(В)=(D), где матрица А:

матрица B:

матрица D:

 

 

 

Применив тригонометрические преобразования, сигнал на выходе НЭ запишем в следующей форме:

 

 

Итак,

 

 

 

 

Рисунок 58 – Сигнал на выходе НЭ

 

 

 

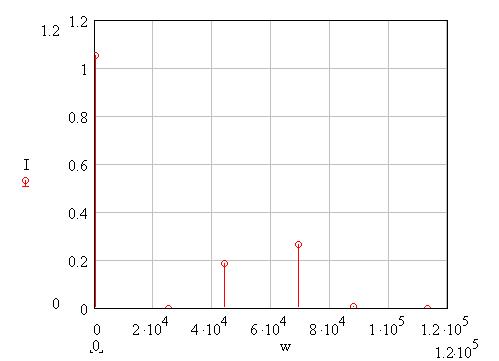
Рисунок 59 – Спектр тока на выходе НЭ

 

Из рисунка и приведенного выше выражения видны следующие нелинейности ВАХ при гармоническом воздействии:

- ток покоя i(U0) получает приращение, обусловленное коэффициентами a2,a4… при четных степенях полинома.

- амплитуда I1 гармоники основной частоты ω1 связана с амплитудой возбуждения Um нелинейным соотношением, обусловленным нечетными степенями полинома.

- ток i(t) содержит высшие гармоники с частотами nω1, кратными частоте воздействия ω1.

 

Кусочно-линейная аппроксимация

Этот вид аппроксимации используется при больших по амплитуде входных сигналах, при этом реальную характеристику заменяют отрезками прямых линий с различными наклонами. Выберем 2 точки, лежащие на линейном участке (2;2,4321) (2,5;4,021) и по ним найдем уравнение прямой.

 

 

Рисунок 60 – Кусочно-линейная аппроксимация НЭ

 

 

По графику определим напряжение отсечки: Uотс=1.175В

На вход нелинейного элемента поступает сигнал u(t) с параметрами: А=5.1В, f=12кГц θ=55˚. Находим рабочую точку:

 

 

Рисунок 61 – Сигнал на входе НЭ

Найдём спектр выходного сигнала:

 

Рисунок 62 – Спектр входного сигнала

 

 

Входное напряжение преобразуется в выходной ток и имеет вид:

 

 

Рисунок 63 – Ток на выходе нелинейного элемента

 

Рисунок 64 - Спектр тока на выходе нелинейного элемента

 

Функции Берга:

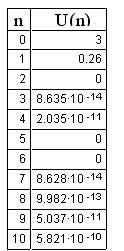
Таблица 6 - Значения функции Берга для n=2..10

Бигармоническое воздействие

На НЭ воздействуют два гармонических сигнала:

Параметры сигналов:

A1=0.11В, f1=7кГц, U₀=1,5В

А2=0,15В, f2=11кГц, U₀=0В

Этот бигармонический сигнал поступает на нелинейный элемент, у которого ВАХ описывается выражением:

 

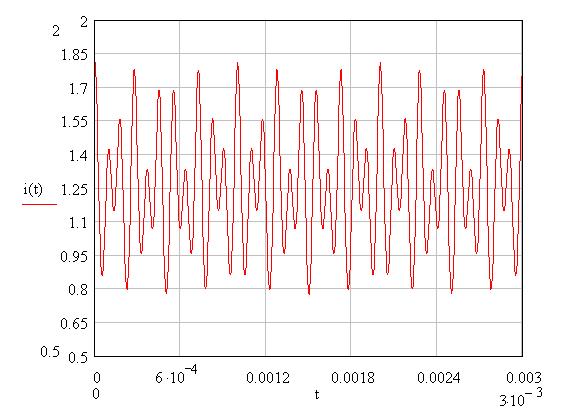
Рисунок 65 – Бигармонический сигнал на входе НЭ

 

Рисунок 66 – Спектр сигнала на входе НЭ

 

Для упрощения рассмотрим слабо нелинейный режим, то есть когда достаточно учитывать только линейный и квадратичный члены полинома.

Получим

 

 

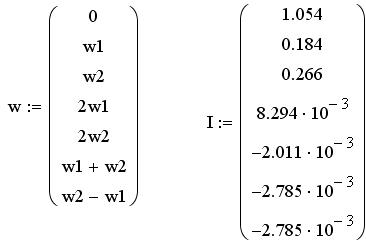
На выходе появляются дополнительные составляющие на кратных, комбинационных частотах, которые можно посчитать по формулам:

 

 

 

 

 

 

 

Рисунок 67 – Спектр бигармонического сигнала на выходе НЭ