
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия в спектре непериодического сигналаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для получения выражения для непериодического сигнала воспользуемся выражением, которое при выполнении условия f(t)=g(t)=s(t), определяет полную энергию сигнала
Это важное соотношение, устанавливающее связь между энергией сигнала (выделяемой на сопротивлении 1ом) и модулем его спектральной плотности, известно под названием равенство Парсеваля. Величина
Энергия данного сигнала:
2.5 Некоторые свойства преобразований Фурье Между сигналом s(t) и его спектром S(ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований сигнала рассмотрим следующие, наиболее важные: сдвиг сигнала во времени, изменение масштаба времени, сложение сигналов, дифференцирование, интегрирование сигнала.
Сдвиг сигнала во времени Пусть сигнал s1(t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1(ω). При задержке этого сигнала на время t0 получим новою функцию времени s(t2)=s(t – t0), существующую на интервале от t1+t0 до t2+t0. Спектральная плотность сигнала s2(t) равна
Из этого соотношения видно, что сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси не зависит.
Сдвиг сигнала во времени осуществляется на величину 0.1Т = 0,169с
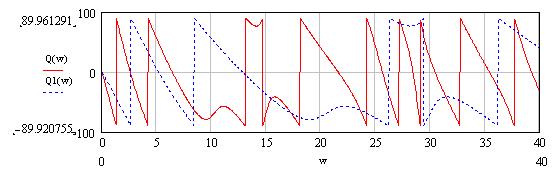
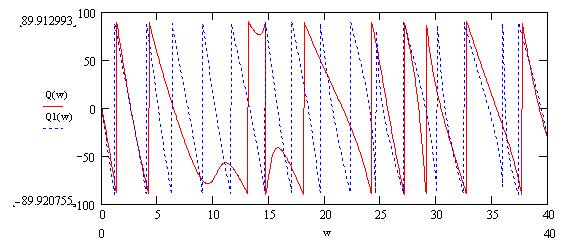
Рисунок 7 – ФЧХ исходного (Q(w)) и задержанного (Q1(w)) сигналов
Вывод: Сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси времени не зависит.
Изменение масштаба времени Пусть сигнал s1(t) подвергается сжатию во времени. Новый сжатый сигнал s2(t) связан с исходным соотношением s2(t)=s1(nt), n>1. Спектральная плотность сжатого импульса
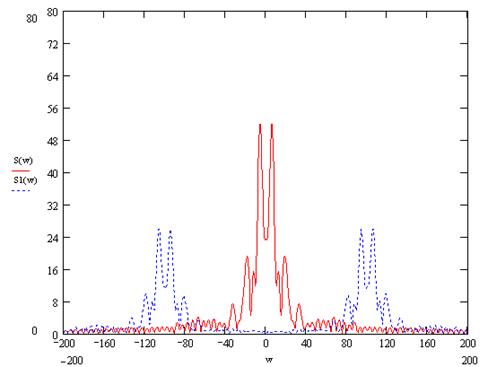
Рисунок 8 – АЧХ исходного(S(w)) и сжатого S1(w) сигналов
Рисунок 9 – ФЧХ исходного(S(w)) и сжатого S1(w) сигналов
Вывод: При сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшится в n раз.
Дифференцирование и интегрирование сигнала Дифференцирование сигнала s1(t) можно трактовать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Но производная функции еiωt равна iωeiωt, из чего непосредственно вытекает следующие соответствия:
Рисунок 10 – АЧХ исходного (S(w)) и интегрированного (Si(w)) сигналов
Рисунок 11 – АЧХ исходного (S(w)) и дифференцированного (Sd(w)) сигналов
Рисунок 12 – ФЧХ исходного (S1(w)), дифференцированного (Sd(w)), интегрированного (Si(w)) сигналов
Выводы: Спектр продифференцированного сигнала отличается от спектра исходного сигнала множителем iω. При дифференцировании скорость изменения сигнала во времени возрастает. Как следствие модуль спектра производной имеет большие значения в области высоких частот по сравнению с модулем спектра исходного сигнала. При интегрировании происходит ослабление высокочастотных спектральных составляющих.
Сложение с прямоугольным импульсом А = 0. 11 В, τ = 1.3с, tи = 1,69с
Рисунок 13 – АЧХ исходного сигнала (S(w)), прямоугольного импульса (S1(w)) и суммарного сигнала (As(w))
Рисунок 14 - ФЧХ исходного сигнала (Q(w)), прямоугольного импульса (Q1(w)) и суммарного сигнала (Qs(w)) Вывод: Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным, очевидно, что при сложении сигналов s1(t), s2(t),…, обладающих спектрами S1(ω), S2(ω),…, суммарному сигналу s(t)=s1(t) + s2(t) + … соответствует спектр S(ω)=S1(ω) + S2(ω) + ….
Расщепление сигнала Возьмём ω0= 100
Рисунок 15 – АЧХ исходного (S(w)) и расщепленного (S1(w)) сигналов
Рисунок 16 – ФЧХ исходного (S(w)) и расщепленного (S1(w)) сигналов Между сигналом
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.77 (0.006 с.) |



 имеет смысл энергии приходящейся на 1 Гц и рассматривается как спектральная плотность энергии.
имеет смысл энергии приходящейся на 1 Гц и рассматривается как спектральная плотность энергии.



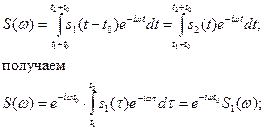

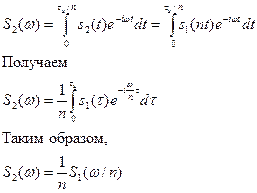 n= 2
n= 2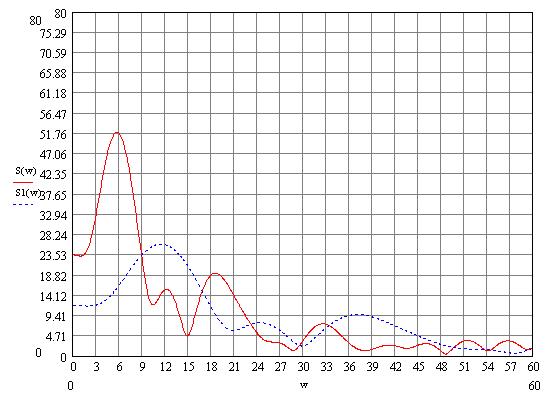
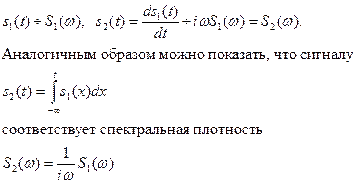





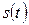 и его спектром
и его спектром 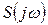 существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из возможных преобразований сигнала рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг сигнала во времени, изменение масштаба времени, дифференцирование и интегрирование сигнала, сложение и произведение сигналов.
существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из возможных преобразований сигнала рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг сигнала во времени, изменение масштаба времени, дифференцирование и интегрирование сигнала, сложение и произведение сигналов.


