
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение характеристик случайных сигналовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Анализ различных задач радиотехники показывает, что по существу любой сигнал, несущий информацию, может рассматриваться как случайный (стохастический). Это обусловливается, с одной стороны, случайными искажениями сигнала при его распространении и наличием разнообразных (внешних и внутренних) помех, а с другой—несовершенством применяемых радиотехнических устройств и систем. Ряд процессов, влияющих на их технический уровень и качество, относится к категории случайных. Экспериментальный анализ таких процессов также связан с измерением характеристик соответствующих случайных сигналов. Изучение свойств и характеристик случайных сигналов базируется, как известно, на теории вероятностей и математической статистике. Потребность в этом привела к развитию методов и средств, составляющих содержание статистических измерений. Они основаны на общих принципах измерения параметров сигналов, но имеют свою специфику и ряд принципиальных особенностей, вытекающих из теории случайных процессов. Напомним исходные определения и сведения о характеристиках случайных сигналов и уточним основные задачи техники статистических измерений.
ОБЩИЕ СВЕДЕНИЯ Случайным называется сигнал, мгновенные значения которого изменяются во времени случайным образом. В связи с этим он описывается случайной функцией времени X(t), которую можно рассматривать как бесконечную совокупность (ансамбль) функций xi(t), каждая из которых представляет собой одну из возможных реализаций X(t). На рис. 8.1 в качестве примера приведена совокупность реализаций xi(t), где xi(tj)—мгновенное значение сигнала X(t), соответствующее значению i -й реализации в j -й момент времени. Полное описание случайных сигналов может быть произведено с помощью системы вероятностных характеристик. Любая из них определяется либо усреднением по совокупности реализаций xi(t), либо усреднением по времени для одной реализации X(t). В общем случае результаты таких усреднений неодинаковы, они могут зависеть либо не зависеть от времени или номера реализации. Наличие или отсутствие этой зависимости определяет такие фундаментальные свойства сигналов, как стационарность и эргодичность. Стационарным называется сигнал, вероятностные характеристики которого не зависят от времени. Соответственно вероятностные характеристики эргодических сигналов не зависят от номера реализации.
Классификация случайных сигналов по признакам стационарности и эргодичности позволяет выделить следующие их виды: стационарные эргодические, стационарные неэргодические, нестационарные эргодические и нестационарные неэргодические. В рамках курса мы ограничимся рассмотрением методов и средств измерения вероятностных характеристик случайных сигналов первого вида как наиболее простого и типичного. Для таких сигналов усреднение любой вероятностной характеристики по множеству реализаций эквивалентно усреднению повремени одной теоретически бесконечно длинной реализации. Другими словами все вероятностные характеристики стационарного эргодического сигнала могут быть получены по одной его реализации. Ясно, что проводить измерения с одной реализацией сигнала значительно проще, чем с совокупностью реализаций. Для практических приложений наиболее важны следующие вероятностные характеристики стационарных эргодических сигналов, имеющих длительность реализации Т (ГОСТ 16465—70): среднее значение (математическое ожидание), характеризующее, как и
Рис. 8.1. Совокупность реализаций случайного сигнала.
для детерминированных сигналов (см. § 3.1), постоянную составляющую сигнала
средняя мощность, характеризующая энергетический уровень сигнала,
дисперсия, характеризующая среднюю мощность переменной составляющей (флюктуации) сигнала,
или среднее квадратическое отклонение его
функция распределения, определяемая как интегральная вероятность того что значение Xi(tj) ниже некоторого заданного уровня х,
т. е. для стационарных эргодических сигналов Fx характеризуется относительным временем пребывания значений реализации ниже уровня х ( одномерная плотность вероятности, называемая также дифференциальным законом распределения,
где
корреляционная функция, характеризующая стохастическую связь между мгновенными значениями случайного сигнала, разделенными заданным интервалом времени
или нормированная корреляционная функция
взаимная корреляционная функция, характеризующая стохастическую связь между мгновенными значениями двух случайных сигналов X(t) и Y(t), разделенными интервалом времени
и соответствующая ей нормированная взаимная корреляционная функция
спектральная плотность мощности, определяющая среднюю мощность сигнала, приходящуюся на единицу полосы частот. Распределение средней мощности по частоте характеризует энергетический спектр сигнала. Он может быть определен для каждой реализации xi(t) по общим правилам (см. § 7.8). Оказывается, что для стационарных случайных сигналов функция спектральной плотности мощности
Если мы имеем два стационарных сигнала X(t) и Y(t), они могут быть охарактеризованы взаимной спектральной плотностью мощности, которая в общем случае является комплексной величиной
При расчетах по формулам (8.11) и (8.12) можно пользоваться значениями Как следует из формул (8.1) — (8.12), все вероятностные характеристики, представляющие собой неслучайные числа или функции, определяются по одной реализации X(t) бесконечной длительности. Практически же длительность Т, называемая продолжительностью анализа, всегда ограничена. Поэтому реально всякая экспериментальная характеристика отличается от соответствующей вероятностной (теоретической) характеристики и может являться только ее оценкой. Оценки, полученные аппаратурным путем, называются статистическими характеристиками и обозначаются знаком «
|
||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.61.163 (0.012 с.) |


 (8.1)
(8.1) (8.2)
(8.2) (8.3)
(8.3) (8.4)
(8.4) (8.5)
(8.5) — i -й интервал пребывания; п — количество интервалов);
— i -й интервал пребывания; п — количество интервалов); (8.6)
(8.6) — расстояние между соседними уровнями Xi(tj) и
— расстояние между соседними уровнями Xi(tj) и  , называемое дифференциальным коридором, а
, называемое дифференциальным коридором, а  — i -й интервал пребывания реализации в пределах этого коридора;
— i -й интервал пребывания реализации в пределах этого коридора; ,
, (8.7)
(8.7) (8.8)
(8.8)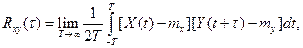 (8.9)
(8.9) (8.10)
(8.10) связана с корреляционной функцией парой преобразований Фурье (теорема Винера — Хинчина):
связана с корреляционной функцией парой преобразований Фурье (теорема Винера — Хинчина): (8.11)
(8.11)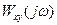 . Поэтому на практике определяют функции действительной и мнимой составляющих
. Поэтому на практике определяют функции действительной и мнимой составляющих  (8.12)
(8.12) и
и  . Тогда функции спектральной плотности мощности будут нормированными.
. Тогда функции спектральной плотности мощности будут нормированными. » (см. § 1.3). В этом смысле измерение характеристик случайных сигналов всегда сопровождается статистическими погрешностями. В остальном метрологические характеристики анализаторов статистических характеристик аналогичны характеристикам приборов других подгрупп и регламентируются ГОСТ 8.251—77. Анализаторы статистических характеристик входят в подгруппу X (см. § 2.1), где они образуют вид Х6.
» (см. § 1.3). В этом смысле измерение характеристик случайных сигналов всегда сопровождается статистическими погрешностями. В остальном метрологические характеристики анализаторов статистических характеристик аналогичны характеристикам приборов других подгрупп и регламентируются ГОСТ 8.251—77. Анализаторы статистических характеристик входят в подгруппу X (см. § 2.1), где они образуют вид Х6.


