
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод интерференционных фигурСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При подаче на входы Y и X двух синхронных синусоидальных напряжений луч на экране ЭЛТ совершает сложное движение, и траектория луча воспринимается нами как неподвижная интерференционная фигура (фигура Лиссажу). Вид ее зависит от кратности Табл. 7.2. Примеры интерференционных фигур
Из табл. 7.2 видно, что, независимо от значения
откуда по результатам подсчета Чем сложнее фигура, тем затруднительнее становится применять рассмотренное правило. Поэтому при практических измерениях нужно всегда стремиться к простейшему виду фигуры — эллипсу, когда Метод круговой развертки Круговую развертку целесообразно применять при Этим методом можно измерять и частоту следования импульсов. Однако при дробно-рациональном отношении частот (например, 3/2) результаты измерений могут оказаться неоднозначными. Поэтому такие измерения следует проводить только с импульсами отрицательной полярности. Они создают разрывы на изображении окружности, которые при дробном отношении частот не наблюдаются (разрывы, полученные при первом обороте луча, будут засвечены при последующих оборотах).
ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА
Наиболее распространенным методом измерения
Перед измерением h и Н необходимо совместить центр эллипса с началом координат шкалы. Для этого поочередно отключают напряжения Результаты измерения
при Второй метод измерения
Если, кроме того, амплитуды
В практике измерений
|
||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.161.122 (0.009 с.) |

 , соотношения амплитуд напряжений и фазового сдвига между ними. Полагая равными амплитуды напряжений (обеспечивается регулировкой усиления в УВО и УГО), приведем примеры интерференционных фигур для различных значений
, соотношения амплитуд напряжений и фазового сдвига между ними. Полагая равными амплитуды напряжений (обеспечивается регулировкой усиления в УВО и УГО), приведем примеры интерференционных фигур для различных значений  (табл. 7.2).
(табл. 7.2).
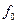 и
и  соотношением
соотношением
 и
и  и измерения
и измерения 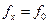 . Однако чем выше
. Однако чем выше  , что расширяет возможности измерения больших
, что расширяет возможности измерения больших  с помощью осциллографа является метод эллипса. Эллипс является частным случаем интерференционной фигуры при
с помощью осциллографа является метод эллипса. Эллипс является частным случаем интерференционной фигуры при 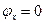 и
и  либо превращаться в окружность (круговая развертка) при
либо превращаться в окружность (круговая развертка) при  . Методика измерения
. Методика измерения 
 и
и  и совмещают середины горизонтальной и вертикальной линий (создаваемых соответственно
и совмещают середины горизонтальной и вертикальной линий (создаваемых соответственно  не вносит заметной погрешности, либо, наоборот, оценить
не вносит заметной погрешности, либо, наоборот, оценить 



 и
и  равны, то
равны, то
 как опорным. Методика измерения
как опорным. Методика измерения  ,но теперь измеряется угловое положение светящейся полуокружности, создаваемой напряжением
,но теперь измеряется угловое положение светящейся полуокружности, создаваемой напряжением  при подаче на вход Z.
при подаче на вход Z.


