
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифровые анализаторы спектраСодержание книги
Поиск на нашем сайте
Исходной предпосылкой цифровых методов спектрального анализа является теорема Котельникова (см. § 3.6.1). Сигнал, спектр которого ограничен сверху частотой Под ДПФ понимается цифровое моделирование прямого преобразования Фурье (7.9), которое в общем случае описывается соотношением
где N — число учитываемых отсчетов сигнала, определяемое для времени анализа Из (7.11) следует, что при выполнении процедуры ДПФ необходимо осуществить следующие операции: выборку с заданным интервалом генерирование весовых коэффициентов умножение (или взвешивание) мгновенных значений Ux(t) на весовые коэффициенты в требуемой последовательности; суммирование полученных произведений для каждого значения частоты из множества рабочих частот. Образованная взвешенная сумма F(p) является дискретной оценкой комплексного аппаратурного спектра, который далее может быть пересчитан в амплитудный и фазовый спектры.
Рис. 7.38. Структурная схема цифрового АС.
уделяется разработке экономичных алгоритмов, позволяющих значительно уменьшить Сущность БПФ сводится к тому, что последовательность из N отсчетов разбивается на m более коротких подпоследовательностей. Для каждой такой подпоследовательности требуется выполнять уже не N2 операций комплексного умножения и суммирования (в расчете на вычисление амплитудного и фазового спектров), а В преселектор входят все каскады АС от входной цепи до АЦП. Он имеет полосу пропускания, равную полосе обзора АС, и обеспечивает фильтрацию Ux(t). Дискретизация Ux(t) осуществляется в АЦП, причем импульсный преобразователь образует решетчатую копию Ux(t) с интервалом дискретизации
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.151.180 (0.046 с.) |

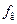 , полностью описывается отсчетами через интервалы времени
, полностью описывается отсчетами через интервалы времени  (решетчатая копия непрерывного сигнала). С помощью дискретного преобразования Фурье (ДПФ) совокупность временных отсчетов может быть пересчитана в комплексный дискретный спектр и далее в амплитудный и фазовый спектры.
(решетчатая копия непрерывного сигнала). С помощью дискретного преобразования Фурье (ДПФ) совокупность временных отсчетов может быть пересчитана в комплексный дискретный спектр и далее в амплитудный и фазовый спектры.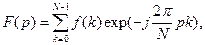 (7.11)
(7.11) как
как  ; f(k) — кодовое представление отсчетов сигнала с помощью безразмерного времени k, связанного с моментами выборки мгновенных значений сигнала
; f(k) — кодовое представление отсчетов сигнала с помощью безразмерного времени k, связанного с моментами выборки мгновенных значений сигнала 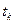 соотношением
соотношением  ;
;  — безразмерная частота.
— безразмерная частота.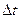 мгновенных значений Ux(t) и их цифровое кодирование;
мгновенных значений Ux(t) и их цифровое кодирование; в том же кодовом представлении;
в том же кодовом представлении;
 ), меньше
), меньше  операций. Тогда весь требуемый объем вычислений может быть выполнен за
операций. Тогда весь требуемый объем вычислений может быть выполнен за  операций, что и обеспечивает возможность сокращения
операций, что и обеспечивает возможность сокращения 


