Измерение фазового сдвига методом
Похожие статьи вашей тематики
СУММЫ И РАЗНОСТИ НАПРЯЖЕНИЙ
Общая идея, положенная в основу рассматриваемого метода, заключается в переносе информации об измеряемом значении  в амплитуду результирующего (суммарного или разностного) напряжения с последующим измерением этого напряжения аналоговым или цифровым вольтметром. Таким образом, фазовые измерения трансформируются в амплитудные, существенно расширяя функции вольтметров и превращая их в амплифазометры. в амплитуду результирующего (суммарного или разностного) напряжения с последующим измерением этого напряжения аналоговым или цифровым вольтметром. Таким образом, фазовые измерения трансформируются в амплитудные, существенно расширяя функции вольтметров и превращая их в амплифазометры.
Действительно, если сигналы, описываемые выражениями (6.2), подать на схему сложения (сумматор), то амплитуда их векторной суммы с учетом (6.3) будет равна

и при 
 (6.7) (6.7)
Аналогично с помощью схемы вычитания можно образовать разностное напряжение, амплитуда которого
 (6.8) (6.8)
Как видно из (6.7) и (6.8), для измерения  достаточно использовать только значение достаточно использовать только значение  , или , или  .Однако такой фазометр будет иметь неравномерную шкалу и резко выраженную зависимость погрешности измерения .Однако такой фазометр будет иметь неравномерную шкалу и резко выраженную зависимость погрешности измерения  от самого значения от самого значения  (в силу свойств функций cos (в силу свойств функций cos  /2 и sin /2 и sin  /2). Результаты измерения /2). Результаты измерения  будут зависеть, кроме того, от будут зависеть, кроме того, от  (хотя эта информация необходима для реализации амплифазометра). Поэтому в практических схемах фазометров (рис. 6.1) осуществляют дополнительные преобразования, используя для этой цели и суммарное, и разностное напряжения. (хотя эта информация необходима для реализации амплифазометра). Поэтому в практических схемах фазометров (рис. 6.1) осуществляют дополнительные преобразования, используя для этой цели и суммарное, и разностное напряжения.
Как видно из рис. 6.1, перед образованием суммарного и разностного напряжений амплитуды  и и  уравниваются с помощью ВУ1 и ВУ2, а дополнительные преобразования сводятся либо к делению уравниваются с помощью ВУ1 и ВУ2, а дополнительные преобразования сводятся либо к делению  на на  (рис. 6.1, а), либо к образованию разности (рис. 6.1, а), либо к образованию разности 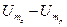 (рис. 6.1, б). В первом случае в качестве ИУ фазометра применяется ИО, рассмотренный в § 3.5.5, а во втором — дополнительная схема вычитания с вольтметром. (рис. 6.1, б). В первом случае в качестве ИУ фазометра применяется ИО, рассмотренный в § 3.5.5, а во втором — дополнительная схема вычитания с вольтметром.
Если в схеме рис. 6.1, а разностное напряжение подать на вход канала делимого ИО, а суммарное — на вход канала делителя, то показание ИО, согласно (6.7) и (6.8), будет пропорционально
 (6.9) (6.9)
Из (6.9) видно, что результаты измерения  уже не зависят от уже не зависят от  .Кроме того, неравномерность шкалы и зависимость погрешности измерения от .Кроме того, неравномерность шкалы и зависимость погрешности измерения от  значительно уменьшаются, так как функция tg значительно уменьшаются, так как функция tg  /2 более линейна, чем, например, sin /2 более линейна, чем, например, sin  /2. Однако, поскольку пределы измерения ИО ограничены, диапазон измеряемых /2. Однако, поскольку пределы измерения ИО ограничены, диапазон измеряемых  меньше 0...± меньше 0...± 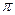 . .
Недостатки схемы рис. 6.1, а устраняются в схеме рис. 6.1, б, где образуется разность

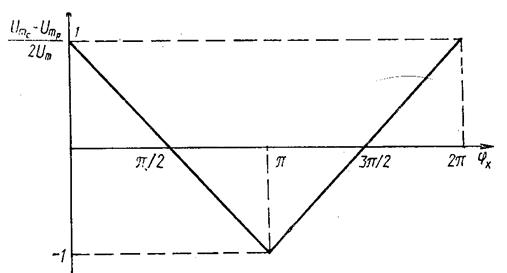
На рис. 6.2 приведен график зависимости  от от  , из которого видно, что при применении вольтметра с нулем посредине шкалы и , из которого видно, что при применении вольтметра с нулем посредине шкалы и

Рис. 6.1. Структурные схемы фазометров, реализующих метод суммы и разности напряжении:
а — с измерителем отношения; б — с фазовым детектором.
Рис. 6.2. Градуировочная характеристика фазометра с фазовым детектором.
предварительной калибровке фазометра для устранения зависимости  пределы измерения пределы измерения  расширяются до 0...2 расширяются до 0...2 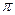 , а шкала фазометра является равномерной. , а шкала фазометра является равномерной.
Оба варианта фазометра могут быть реализованы в диапазонах ВЧ и СВЧ. На ВЧ применяются типовые схемы сложения и вычитания (пассивные и активные), ИО работает на частоте сигналов  и и  , а в качестве измерителя , а в качестве измерителя  чаще всего применяется ФД с магнитоэлектрическим прибором. В диапазоне СВЧ схемы сложения и вычитания представляют собой гибридные соединения типа восьми- и двенадцатиполюсников, свойства и характеристики которых рассматриваются в курсе «Антенны и устройства СВЧ». Между ними и измерительной частью фазометра включаются детекторы СВЧ сигналов, квадратичный закон детектирования которых должен учитываться при анализе работы фазометра. чаще всего применяется ФД с магнитоэлектрическим прибором. В диапазоне СВЧ схемы сложения и вычитания представляют собой гибридные соединения типа восьми- и двенадцатиполюсников, свойства и характеристики которых рассматриваются в курсе «Антенны и устройства СВЧ». Между ними и измерительной частью фазометра включаются детекторы СВЧ сигналов, квадратичный закон детектирования которых должен учитываться при анализе работы фазометра.
Основное применение рассмотренного метода — разработка на его основе аналоговых фазометров, работающих в диапазонах ВЧ и СВЧ и обеспечивающих измерение  с основной погрешностью порядка ±2,5°. с основной погрешностью порядка ±2,5°.
Преобразование частоты в фазометрах
Фазометры, в которых сигналы  и и  непосредственно смешиваются и сравниваются, называются гомодинными. Хотя они просты в схемном отношении, но далеко не всегда оптимальны. Действительно, измерительные преобразователи в схемах рис. 6.1 широкодиапазонные, что отрицательно сказывается на их характеристиках и параметрах фазометра в целом. Значительно лучшие параметры будет иметь фазометр, в котором все преобразования производятся на одной частоте. Это становится возможным, если воспользоваться принципами супергетеродинного приема, предполагающего перенос частоты непосредственно смешиваются и сравниваются, называются гомодинными. Хотя они просты в схемном отношении, но далеко не всегда оптимальны. Действительно, измерительные преобразователи в схемах рис. 6.1 широкодиапазонные, что отрицательно сказывается на их характеристиках и параметрах фазометра в целом. Значительно лучшие параметры будет иметь фазометр, в котором все преобразования производятся на одной частоте. Это становится возможным, если воспользоваться принципами супергетеродинного приема, предполагающего перенос частоты  и и  на некоторую промежуточную частоту. на некоторую промежуточную частоту.
Достоинства супергетеродинного приема широко используются в радиоизмерительной технике. Мы уже знакомы с конкретными примерами, когда гетеродинное преобразование частоты позволяет осуществить частотную селекцию входного сигнала (в селективных вольтметрах) или расширить диапазон измерений (в ЦЧ). Покажем, что перенос частоты входных сигналов в фазометрах не только расширяет их частотный диапазон, но и не вносит дополнительных погрешностей в результат измерения  . .
Если в дополнение к сигналам (6.2) образовать гетеродинный сигнал
 (6.10) (6.10)
подать попарно сигналы  , , 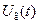 и и  , ,  на соответствующие смесители, а затем выделить с помощью УПЧ напряжения разностной частоты, то на соответствующие смесители, а затем выделить с помощью УПЧ напряжения разностной частоты, то
 (6.11) (6.11)
где  и и  — фазовые сдвиги в трактах преобразования частоты. При идентичных фазовых характеристиках этих трактов — фазовые сдвиги в трактах преобразования частоты. При идентичных фазовых характеристиках этих трактов  и, как следует из (6.11) и (6.3), фазовый сдвиг между сигналами и, как следует из (6.11) и (6.3), фазовый сдвиг между сигналами  и и  по-прежнему равен по-прежнему равен  .Таким образом, само гетеродинное преобразование частоты, действительно, не вносит дополнительной погрешности в результат измерения .Таким образом, само гетеродинное преобразование частоты, действительно, не вносит дополнительной погрешности в результат измерения  . Гетеродинный сигнал (6.10) может быть образован путем непрерывного линейного изменения фазы одного из входных сигналов или с помощью гетеродина. . Гетеродинный сигнал (6.10) может быть образован путем непрерывного линейного изменения фазы одного из входных сигналов или с помощью гетеродина.
Первый способ реализуется с помощью фазовращателя (ФВ), включаемого, например, в первый (опорный) канал фазометра и управляемого таким образом, что начальная фаза выходного сигнала ФВ  , где , где  — скорость изменения — скорость изменения  . В этом случае фаза выходного сигнала ФВ . В этом случае фаза выходного сигнала ФВ  а частота а частота  . Если теперь преобразованный и второй сигналы подать на смеситель, то дальнейшие преобразования будут выполняться на частоте . Если теперь преобразованный и второй сигналы подать на смеситель, то дальнейшие преобразования будут выполняться на частоте  . Этот способ позволяет избежать применения специального гетеродина, но эффективен при измерении только постоянных или медленно меняющихся . Этот способ позволяет избежать применения специального гетеродина, но эффективен при измерении только постоянных или медленно меняющихся  . .
Наиболее распространенным является второй способ, который не только позволяет создавать широкодиапазонные фазометры, но и обеспечивает автоматизацию исследования ФЧХ, если в качестве гетеродина используется генератор качающейся частоты (ГКЧ). Особенностью ГКЧ фазометров является их двухканальность: один канал используется в качестве гетеродина, а второй — в качестве источника измерительных сигналов, подаваемых на вход исследуемой цепи. Разность частот сигналов на выходах обоих каналов поддерживается постоянной и равной промежуточной частоте фазометра.
В широкодиапазонных фазометрах применяется также стробоскопическое преобразование частоты. Гетеродинный сигнал в этом случае представляет собой последовательность коротких строб-импульсов, а в качестве смесителя применяется диодная ключевая схема с накопителем. Стробоскопическое преобразование позволяет получить коэффициент
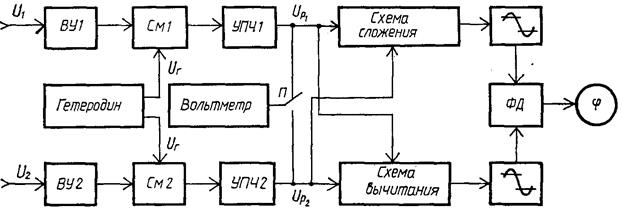
Рис. 6.3. Структурная схема фазометра с преобразованием частоты.
перекрытия по частоте в пределах 100...1000 без сменных гетеродинов и смесителей.
Структурная схема фазометра с общим гетеродином и измерителем  на основе ФД приведена на рис. 6.3. Суммарное и разностное напряжения ограничиваются по амплитуде, и входные напряжения ФД имеют форму меандра с нормированной амплитудой. Это автоматически устраняет зависимость на основе ФД приведена на рис. 6.3. Суммарное и разностное напряжения ограничиваются по амплитуде, и входные напряжения ФД имеют форму меандра с нормированной амплитудой. Это автоматически устраняет зависимость  и применяется во всех современных фазометрах. В то же время обеспечивается возможность поочередного измерения амплитудных значений и применяется во всех современных фазометрах. В то же время обеспечивается возможность поочередного измерения амплитудных значений  и и  с частотной селекцией, как в селективных вольтметрах. с частотной селекцией, как в селективных вольтметрах.
НУЛЕВОЙ МЕТОД
Нулевой метод как основная модификация метода сравнения распространен при измерении не только амплитудных и частотно-временных параметров сигналов, но также и фазовых параметров их. Поясним сущность и особенности нулевого метода измерения  с помощью рис. 6.4, где ИФВ — измерительный фазовращатель вида ФЗ, используемый в качестве образцовой меры с помощью рис. 6.4, где ИФВ — измерительный фазовращатель вида ФЗ, используемый в качестве образцовой меры  , ФВ необходим для предварительной калибровки фазометра, а в качестве ИУ могут быть использованы индикаторы равенства фаз , ФВ необходим для предварительной калибровки фазометра, а в качестве ИУ могут быть использованы индикаторы равенства фаз  и и  , противофазности или квадратурности их. , противофазности или квадратурности их.
С помощью ИФВ начальная фаза сигнала  , принимаемого за опорный, может изменяться (запаздывать) на величину , принимаемого за опорный, может изменяться (запаздывать) на величину  . Тогда с помощью ИУ можно зафиксировать величину . Тогда с помощью ИУ можно зафиксировать величину  . Если . Если  , то , то 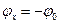 , т. е. измеряемое значение , т. е. измеряемое значение  прямо отсчитывается по шкале ИФВ. При прямо отсчитывается по шкале ИФВ. При   , а при , а при   . Можно в принципе измерять любое промежуточное значение . Можно в принципе измерять любое промежуточное значение  , но тогда будет реализован уже не нулевой, а дифференцированный метод измерения , но тогда будет реализован уже не нулевой, а дифференцированный метод измерения  . Он не применяется в практике фазовых измерений, так как для измерения . Он не применяется в практике фазовых измерений, так как для измерения  необходим дополнительный фазометр, который не только усложняет прибор, но и увеличивает погрешность измерения необходим дополнительный фазометр, который не только усложняет прибор, но и увеличивает погрешность измерения  . В то же время индикаторы значений . В то же время индикаторы значений  , равных 0, 90или 180°, реализуются достаточно просто и погрешности в результат измерения , равных 0, 90или 180°, реализуются достаточно просто и погрешности в результат измерения  практически не вносят. практически не вносят.

| | | | | | | | Рис. 6.4. Структурная схема аналогового фазометра, реализующего нулевой метод.
| | | | Рис. 6.5. Структурная схема цифрового фазометра, реализующего нулевой метод.
| | | |
В качестве индикатора значений  , равных , равных  и и 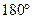 , чаще всего применяется осциллограф. При подаче , чаще всего применяется осциллограф. При подаче  и и  на входы на входы  и и 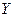 осциллографа наблюдаемая интерференционная фигура будет иметь вид эллипса, параметры которого определяются значением осциллографа наблюдаемая интерференционная фигура будет иметь вид эллипса, параметры которого определяются значением  . Если . Если  , то эллипс «стягивается» в линию, которая наклонена вправо. При , то эллипс «стягивается» в линию, которая наклонена вправо. При  линия будет наклонена влево. Момент «стягивания» эллипса в линию может быть зафиксирован очень точно. линия будет наклонена влево. Момент «стягивания» эллипса в линию может быть зафиксирован очень точно.
Индикатор значения  аналогичен измерителю аналогичен измерителю  в схемах рис. 6.1, б и 6.3. Как видно из рис. 6.2, в момент в схемах рис. 6.1, б и 6.3. Как видно из рис. 6.2, в момент  выходное напряжение ФД равно нулю, что также точно фиксируется магнитоэлектрическим прибором. выходное напряжение ФД равно нулю, что также точно фиксируется магнитоэлектрическим прибором.
В заключение подчеркнем роль установочного ФВ, позволяющего скомпенсировать неидентичность фазовых характеристик каналов фазометра в процессе его предварительной калибровки. При калибровке на оба входа фазометра подается сигнал  ,а ИФВ устанавливается в начальное положение ,а ИФВ устанавливается в начальное положение  . Изменяя фазовый сдвиг, вносимый ФВ, фиксируют значение . Изменяя фазовый сдвиг, вносимый ФВ, фиксируют значение  ,и на этом калибровка фазометра заканчивается. ,и на этом калибровка фазометра заканчивается.
Процесс измерения  в фазометрах, реализующих нулевой метод, достаточно легко автоматизируется. Такие фазометры, аналогичные автокомпенсационным вольтметрам (см. § 3.5.2),реализуются как цифровые приборы. Типовая структурная схема автокомпенсационного цифрового фазометра (ЦФ) приведена на рис. 6.5. Видно, что ЦФ включает узлы схемы рис. 6.4, а конкретным объектом автоматизации является ИФВ, управляемый через УУ выходным напряжением ФД. В момент компенсации (при в фазометрах, реализующих нулевой метод, достаточно легко автоматизируется. Такие фазометры, аналогичные автокомпенсационным вольтметрам (см. § 3.5.2),реализуются как цифровые приборы. Типовая структурная схема автокомпенсационного цифрового фазометра (ЦФ) приведена на рис. 6.5. Видно, что ЦФ включает узлы схемы рис. 6.4, а конкретным объектом автоматизации является ИФВ, управляемый через УУ выходным напряжением ФД. В момент компенсации (при  ) код на входе ИФВ отражает измеряемое значение ) код на входе ИФВ отражает измеряемое значение  и фиксируется с помощью цифрового ОУ. Сам ИФВ может быть аналоговым или дискретным. В первом случае в код должен быть преобразован угол поворота ИФВ, и уравновешивание фаз и фиксируется с помощью цифрового ОУ. Сам ИФВ может быть аналоговым или дискретным. В первом случае в код должен быть преобразован угол поворота ИФВ, и уравновешивание фаз  и и  является равномерным. Во втором случае появляется возможность реализовать поразрядное уравновешивание фаз по аналогии с ЦВ (см. § 3.6.2). Для этого ИФВ должен представлять собой цепочку последовательно включенных ФВ является равномерным. Во втором случае появляется возможность реализовать поразрядное уравновешивание фаз по аналогии с ЦВ (см. § 3.6.2). Для этого ИФВ должен представлять собой цепочку последовательно включенных ФВ 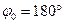 (старший разряд), (старший разряд), 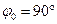 (следующий разряд) и далее с дискретом (следующий разряд) и далее с дискретом  . .
Нулевой метод относится к числу самых точных и широкодиапазонных методов измерения  . Погрешность измерения . Погрешность измерения  , как видно из рис. 6.4 и 6.5, в основном определяется параметрами ИФВ, а известные типы ИФВ позволяют создавать гомодинные фазометры в диапазонах ВЧ и СВЧ. Поэтому на базе нулевого метода разработаны государственные специальные эталоны единицы фазового сдвига в диапазонах ВЧ (ГОСТ 8.139—75) и СВЧ (ГОСТ 8.194— 76 и ГОСТ 8.416—81). Они обеспечивают воспроизведение единицы Ф при СКО не более 0,01° на ВЧ и не более 0,1° на СВЧ. Этот же порядок имеет неисключенная систематическая погрешность, определяемая параметрами ИФВ. , как видно из рис. 6.4 и 6.5, в основном определяется параметрами ИФВ, а известные типы ИФВ позволяют создавать гомодинные фазометры в диапазонах ВЧ и СВЧ. Поэтому на базе нулевого метода разработаны государственные специальные эталоны единицы фазового сдвига в диапазонах ВЧ (ГОСТ 8.139—75) и СВЧ (ГОСТ 8.194— 76 и ГОСТ 8.416—81). Они обеспечивают воспроизведение единицы Ф при СКО не более 0,01° на ВЧ и не более 0,1° на СВЧ. Этот же порядок имеет неисключенная систематическая погрешность, определяемая параметрами ИФВ.
Измерительные фазовращатели
 Классификация типов ИФВ как приборов вида ФЗ достаточно обширна. В диапазоне ВЧ это RС-фазовращатели, индуктивные и емкостные, а в диапазоне СВЧ — фазовращатели на удлинителях, отражательные, диэлектрические и поляризационные. Рассмотрим в качестве примеров наиболее распространенные типы ИФВ: RC — фазовращатели, фазовращатели на удлинителях и диэлектрические ФВ. Классификация типов ИФВ как приборов вида ФЗ достаточно обширна. В диапазоне ВЧ это RС-фазовращатели, индуктивные и емкостные, а в диапазоне СВЧ — фазовращатели на удлинителях, отражательные, диэлектрические и поляризационные. Рассмотрим в качестве примеров наиболее распространенные типы ИФВ: RC — фазовращатели, фазовращатели на удлинителях и диэлектрические ФВ.
 Простейшим RC-фазовращателем является элементарная RС-цепь, которая может быть дифференцирующей или интегрирующей. С помощью таких цепей можно получить изменение Простейшим RC-фазовращателем является элементарная RС-цепь, которая может быть дифференцирующей или интегрирующей. С помощью таких цепей можно получить изменение  в пределах 0...±90°. Однако характеристики их не удовлетворяют требованиям, предъявляемым к ИФВ. Прежде всего недостаточен диапазон изменения в пределах 0...±90°. Однако характеристики их не удовлетворяют требованиям, предъявляемым к ИФВ. Прежде всего недостаточен диапазон изменения  , так как значения , так как значения  могут изменяться в пределах 0...3600 или 0…±180°. Далее имеет место резкая зависимость могут изменяться в пределах 0...3600 или 0…±180°. Далее имеет место резкая зависимость  . Поэтому элементарные RС-цепи применяются только для создания фиксированных значений . Поэтому элементарные RС-цепи применяются только для создания фиксированных значений  или как функциональные элементы более сложных ИФВ. или как функциональные элементы более сложных ИФВ.
Характерным примером фиксированного RС-фазовращателя является так называемый квадратурный ФВ. Он легко образуется как комбинация дифференцирующей RС-цепи с 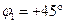 и интегрирующей RС-цепи с и интегрирующей RС-цепи с 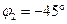 , соединенных в виде шестиполюсника (рис. 6.6). Фазовый сдвиг между , соединенных в виде шестиполюсника (рис. 6.6). Фазовый сдвиг между  и и  равен в этом случае 90° и поддерживается постоянным в широком диапазоне частот. Это достоинство квадратурного ФВ является в ряде случаев принципиальным и используется при проектировании ИФВ в виде фазоразностных RС-цепей, являющихся обобщением шестиполюсника, изображенного на рис. 6.6, на произвольные значения равен в этом случае 90° и поддерживается постоянным в широком диапазоне частот. Это достоинство квадратурного ФВ является в ряде случаев принципиальным и используется при проектировании ИФВ в виде фазоразностных RС-цепей, являющихся обобщением шестиполюсника, изображенного на рис. 6.6, на произвольные значения  и и  . Однако чаще плавное изменение . Однако чаще плавное изменение  в широких пределах при в широких пределах при  достигается с помощью мостовых ФВ. Типовая схема мостового ФВ и векторная диаграмма напряжений, поясняющая работу схемы, приведены на рис. 6.7. достигается с помощью мостовых ФВ. Типовая схема мостового ФВ и векторная диаграмма напряжений, поясняющая работу схемы, приведены на рис. 6.7.
Рис. 6.7. Структурная схема (а) и векторная диаграмма (б) напряжений мостового ФВ.
Как видно из рис. 6.7, а, ФВ представляет собой четырехплечую мостовую цепь, в одну диагональ которой подается 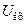 , а с другой диагонали снимается , а с другой диагонали снимается 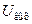 . Если . Если  то делитель то делитель 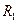 , ,  делит делит 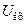 пополам, и точка пополам, и точка  является центром окружности, построенной на является центром окружности, построенной на 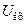 как на диаметре (рис. 6.7, б). Так как сумма векторов как на диаметре (рис. 6.7, б). Так как сумма векторов  и и  также должна быть равна также должна быть равна 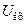 , а угол между ними , а угол между ними 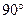 , то точка , то точка  должна двигаться по этой окружности при изменении должна двигаться по этой окружности при изменении  . В результате . В результате 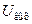 , определяемое вектором ВГ, оказывается постоянным по модулю и равным , определяемое вектором ВГ, оказывается постоянным по модулю и равным  , а по фазе сдвинуто относительно , а по фазе сдвинуто относительно 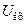 на величину на величину  . При R = 0 . При R = 0  = 0, а при = 0, а при   . Такие ФВ особенно удобны при реализации ИФВ с дискретным поразрядным изменением . Такие ФВ особенно удобны при реализации ИФВ с дискретным поразрядным изменением  . .

Рис. 6.8. Схематическое устройство фазовращателя на удлинителях:
а — телескопический ФВ; б — тромбонный ФВ.
Принцип действия ФВ на удлинителях основан на изменении геометрической длины  линии передачи СВЧ сигнала. Как известно из теории длинных линий, фаза бегущей волны на выходе линии определяется величиной линии передачи СВЧ сигнала. Как известно из теории длинных линий, фаза бегущей волны на выходе линии определяется величиной 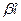 , где , где  (для коаксиалов) или (для коаксиалов) или  (для волноводов) - фазовая постоянная. Таким образом, изменяя (для волноводов) - фазовая постоянная. Таким образом, изменяя  , можно получить ФВ с пределами изменения , можно получить ФВ с пределами изменения  . Практическое применение находят две конструктивные разновидности таких ФВ: телескопический и тромбонный, схематически показанные в волноводном варианте на рис. 6.8. . Практическое применение находят две конструктивные разновидности таких ФВ: телескопический и тромбонный, схематически показанные в волноводном варианте на рис. 6.8.
В диэлектрических ФВ фазовый сдвиг  получают введением в коаксиал или волновод диэлектрика, изменяющего фазовую скорость распространения волны и, следовательно, значение получают введением в коаксиал или волновод диэлектрика, изменяющего фазовую скорость распространения волны и, следовательно, значение  . Характерные примеры диэлектрических ФВ на прямоугольном и круглом волноводах показаны на рис. 6.9. . Характерные примеры диэлектрических ФВ на прямоугольном и круглом волноводах показаны на рис. 6.9.
Если в прямоугольном волноводе распространяется волна 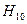 , то максимальный эффект будет получен при размещении диэлектрика в виде пластины посредине широкой стенки волновода (в пучности электрического поля). Конструктивно это можно реализовать с помощью пластинчатого (рис. 6.9, а) или ножевого (рис. 6.9, б) ФВ. Каждый из них имеет свои достоинства и недостатки, но в целом они уступают ФВ на круглом волноводе (рис. 6.9, в). При распространении в нем волны , то максимальный эффект будет получен при размещении диэлектрика в виде пластины посредине широкой стенки волновода (в пучности электрического поля). Конструктивно это можно реализовать с помощью пластинчатого (рис. 6.9, а) или ножевого (рис. 6.9, б) ФВ. Каждый из них имеет свои достоинства и недостатки, но в целом они уступают ФВ на круглом волноводе (рис. 6.9, в). При распространении в нем волны   . С помощью переходов такой ФВ может быть включен в линию передачи любой конструкции. . С помощью переходов такой ФВ может быть включен в линию передачи любой конструкции.
Рис 6.9. Схематическое устройство диэлектрических ФВ.
МЕТОД ПРЕОБРАЗОВАНИЯ ФАЗОВОГО СДВИГА В ИНТЕРВАЛ ВРЕМЕНИ
Как уже неоднократно отмечалось, преобразование измеряемой величины в интервал времени  очень эффективно при построении ЦИП. Широко применяется этот метод и в фазометрии, являясь основным при проектировании большинства типов ЦФ. Суть метода поясняется рис. 6.10. очень эффективно при построении ЦИП. Широко применяется этот метод и в фазометрии, являясь основным при проектировании большинства типов ЦФ. Суть метода поясняется рис. 6.10.
Если с помощью ФУ, аналогичных рис. 5.2, преобразовать гармонические сигналы  и и  (рис. 6.10, а) в короткие импульсы (рис. 6.10, а) в короткие импульсы  и и  (рис. 6.10, б, в), соответствующие моментам перехода (рис. 6.10, б, в), соответствующие моментам перехода  и U2 через нуль в положительном направлении, то интервал времени и U2 через нуль в положительном направлении, то интервал времени
между ближайшими импульсами (рис. 6.10, г) будет пропорционален  . Действительно, по определениям . Действительно, по определениям
 и и 
т. е.
 (6.12) (6.12)
Как видно из (6.12), при измерении  рассматриваемым методом необходимо определять отношение рассматриваемым методом необходимо определять отношение  . Наиболее просто это можно осуществить, если значение . Наиболее просто это можно осуществить, если значение  (называемое еще фазовым интервалом) будет задано не опорным и интервальным импульсами (называемое еще фазовым интервалом) будет задано не опорным и интервальным импульсами  и и  (как в измерителях (как в измерителях  ), а с помощью прямоугольного импульса длительностью ), а с помощью прямоугольного импульса длительностью  . Действительно, из рис. 6.10, г, следует, что в этом случае значение . Действительно, из рис. 6.10, г, следует, что в этом случае значение  может быть определено как постоянная составляющая периодической последовательности прямоугольных импульсов и легко измерено аналоговым или цифровым вольтметром. Если же может быть определено как постоянная составляющая периодической последовательности прямоугольных импульсов и легко измерено аналоговым или цифровым вольтметром. Если же  нужно преобразовать в цифровой код, нужно преобразовать в цифровой код,
то это также легко может быть сделано с помощью селектора, управляемого импульсами  как стробирующими (по аналогии с ЦЧ). В связи с этим во всех фазометрах, реализующих метод преобразования как стробирующими (по аналогии с ЦЧ). В связи с этим во всех фазометрах, реализующих метод преобразования  , предусматривается образование из , предусматривается образование из  и и  периодической последовательности прямоугольных импульсов. Наиболее часто это осуществляется с помощью триггеров, и поэтому такие фазометры называют триггерными. Таким образом, напряжение периодической последовательности прямоугольных импульсов. Наиболее часто это осуществляется с помощью триггеров, и поэтому такие фазометры называют триггерными. Таким образом, напряжение 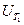 на рис. 6.10, г — это выходное напряжение преобразователя, структурная схема которого показана на рис. 6.11, а. на рис. 6.10, г — это выходное напряжение преобразователя, структурная схема которого показана на рис. 6.11, а.
В практических схемах фазометров могут фиксироваться моменты перехода  и и  через нуль не только в положительном, но и в отрицательном направлениях. Такие фазометры называются двухполупериодными и имеют преобразователь через нуль не только в положительном, но и в отрицательном направлениях. Такие фазометры называются двухполупериодными и имеют преобразователь  ,структурная схема которого показана на рис. 6.11, б, а дополнительные временные диаграммы — на рис. 6.10, д, ж ,структурная схема которого показана на рис. 6.11, б, а дополнительные временные диаграммы — на рис. 6.10, д, ж

Рис. 6.10. Временные диаграммы, поясняющие метод преобразования 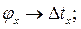
а— входные сигналы  , и , и  ; б — короткие импульсы, соответствующие моментам перехода ; б — короткие импульсы, соответствующие моментам перехода  через нуль в положительном направлении; в — короткие импульсы, соответствующие моментам перехода через нуль в положительном направлении; в — короткие импульсы, соответствующие моментам перехода  через нуль в положительном направлении; г — импульсы на выходе триггера однополупериодного фазометра; д — короткие импульсы, соответствующие моментам перехода через нуль в положительном направлении; г — импульсы на выходе триггера однополупериодного фазометра; д — короткие импульсы, соответствующие моментам перехода  через нуль в отрицательном направлении; е —короткие импульсы, соответствующие моментам перехода через нуль в отрицательном направлении; е —короткие импульсы, соответствующие моментам перехода  через нуль в отрицательном направлении; ж — импульсы на выходе второго триггера двухполупериодного фазометра. через нуль в отрицательном направлении; ж — импульсы на выходе второго триггера двухполупериодного фазометра.
.
Рис. 6.11. Структурные схемы преобразователей триггерных фазометров:
а — однополупериодного; б — двухполупериодного.
Классификация ЦФ аналогична классификации ЦВ (см. § 3.6.1) и ЦЧ (см. § 5.3). Среди них выделяют ЦФ, измеряющие значение  за один период за один период  (или даже его часть) — неинтегрирующие ЦФ и измеряющие среднее за интервал времени (или даже его часть) — неинтегрирующие ЦФ и измеряющие среднее за интервал времени  (см. рис. 6.10, г) значение (см. рис. 6.10, г) значение  — интегрирующие ЦФ (ИЦФ). — интегрирующие ЦФ (ИЦФ).
Неинтегрирующие ЦФ
Структурная схема однополупериодного неинтегрирующего ЦФ, реализующая алгоритм (6.12), приведена в упрощенном виде на рис. 6.12. Работа всех функциональных узлов ЦФ нам уже знакома. Поэтому отметим лишь, что с помощью УУобеспечивается синхронизм в этой работе и ограничивается время измерения  значением Т. значением Т.
Рис. 6.12. Структурная схема однополупериодного неинтегрирующего ЦФ.
Как следует из (6.12), измерение  должно проводиться в два этапа: измерение должно проводиться в два этапа: измерение  (переключатель П в положении 1) и измерение Т (положение 2). При первом измерении счетчик зафиксирует (переключатель П в положении 1) и измерение Т (положение 2). При первом измерении счетчик зафиксирует
 (6.13) (6.13)
где  — период следования импульсов ГСчИ. При втором измерении — период следования импульсов ГСчИ. При втором измерении 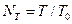 и для вычисления и для вычисления  по результатам измерения по результатам измерения 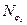 и и 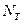 будет справедлива формула будет справедлива формула
 (6.14) (6.14)

Рис. 6.13. Структурные схемы прямоотсчетных неинтегрирующих ЦФ:
а —с умножением частоты входного сигнала; б —с использованием системы АПЧ.
Таким образом, рассмотренный ЦФ является фактически комбинированным прибором (фазометр-частотомер). Двухэтапность процесса измерения и необходимость в дополнительных вычислениях по формуле (6.14) являются его существенными недостатками. Известные способы устранения этих недостатков направлены на достижение кратности периодов  и и  . Действительно, если в формуле (6.13) . Действительно, если в формуле (6.13)  (n=1, 2, 3, …), то мы получаем прямоотсчетный ЦФ. (n=1, 2, 3, …), то мы получаем прямоотсчетный ЦФ.

Рис. 6.14. Структурные схемы прямоотсчетных неинтегрирующих ЦФ:
а —с блоком расширения импульсов; б —с делением частоты входного сигнала.
В этом случае можно идти двумя путями: образованием счетных импульсов с периодом следования  и увеличением времени измерения и увеличением времени измерения  в в  раз (хотя измерения по-прежнему производятся за один период). раз (хотя измерения по-прежнему производятся за один период).
Схемные модификации, позволяющие реализовать первый путь, иллюстрируются рис. 6.13 (для простоты УУ не показано). Как видно из рис. 6.13, а, в первом случае счетные импульсы образуются путем умножения частоты сигнала  в в  раз. Во втором случае (рис. 6.13, б) частота ГСчИ в раз. Во втором случае (рис. 6.13, б) частота ГСчИ в  раз больше частоты входных сигналов, а точное поддержание этого соотношения обеспечивается с помощью системы АПЧ при использовании сигнала раз больше частоты входных сигналов, а точное поддержание этого соотношения обеспечивается с помощью системы АПЧ при использовании сигнала  в качестве опорного. в качестве опорного.
Второй путь также может быть реализован с помощью двух схемных модификаций (рис. 6.14). В первом случае (рис. 6.14, а)для увеличения времени измерения (масштабного преобразования) в схему ЦФ включается дополнительный блок расширения импульсов (БРИ), а счетные импульсы образуются с помощью ФУ из сигнала  .Вторая модификация (рис. 6.14, б)применяется при исследовании ФЧХ четырехполюсников. .Вторая модификация (рис. 6.14, б)применяется при исследовании ФЧХ четырехполюсников.
Интегрирующие ЦФ
По определению в ИЦФ производится измерение среднего значения  за время за время  и не зависящее от и не зависящее от  (поэтому ИЦФ называют еще фазометрами с постоянным временем измерения). Обозначим число фазовых интервалов (поэтому ИЦФ называют еще фазометрами с постоянным временем измерения). Обозначим число фазовых интервалов  ,попадающих в интервал времени ,попадающих в интервал времени  , через , через  .Как видно из рис. 6.10, г, .Как видно из рис. 6.10, г, 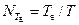 , и счетчик ИЦФ зафиксирует с учетом (6.13) общее число импульсов , и счетчик ИЦФ зафиксирует с учетом (6.13) общее число импульсов
 (6.15) (6.15)
Таким образом, результат измерения  не зависит от не зависит от  ,т. е. устраняется самый существенный недостаток неинтегрирующего ЦФ. Если, кроме того, обеспечить схемным путем выполнение соотношения ,т. е. устраняется самый существенный недостаток неинтегрирующего ЦФ. Если, кроме того, обеспечить схемным путем выполнение соотношения  , то мы получаем прямоотсчетный фазометр. Рассмотрим возможные схемные решения ИЦФ. , то мы получаем прямоотсчетный фазометр. Рассмотрим возможные схемные решения ИЦФ.

Рис. 6.15. Структурная схема однополупериодного ИЦФ.
На рис. 6.15 представлена упрощенная структурная схема однополупериодного ИЦФ, реализующая алгоритм 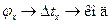 . На выходе селектора 1 образуются пачки счетных импульсов, причем число импульсов в одной пачке равно . На выходе селектора 1 образуются пачки счетных импульсов, причем число импульсов в одной пачке равно 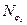 . Эти пачки поступают на вход селектора 2, который открыт во время действия стробирующего импульса. Стробирующий импульс формируется в УУ из импульсов ГСчИ, частота следования которых предварительно понижается в . Эти пачки поступают на вход селектора 2, который открыт во время действия стробирующего импульса. Стробирующий импульс формируется в УУ из импульсов ГСчИ, частота следования которых предварительно понижается в  раз с помощью делителя частоты. Таким образом, раз с помощью делителя частоты. Таким образом,  , а число пачек счетных импульсов, прошедших на выход селектора 2, равно , а число пачек счетных импульсов, прошедших на выход селектора 2, равно  .В результате счетчик фиксирует число импульсов N, прямо определяющее измеряемое значение .В результате счетчик фиксирует число импульсов N, прямо определяющее измеряемое значение  . Комбинируя схемы рис. 6.11, б и рис. 6.15, можно получить двухполупериодный ИЦФ с суммирующим счетчиком. . Комбинируя схемы рис. 6.11, б и рис. 6.15, можно получить двухполупериодный ИЦФ с суммирующим счетчиком.
В практике проектирования ИЦФ наряду со схемой рис. 6.15 широкое применение находит схема, реализующая алгоритм 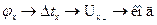 . На возможность такой реализации было указано при характеристике самого метода преобразования . На возможность такой реализации было указано при характеристике самого метода преобразования 
|


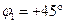 и интегрирующей RС-цепи с
и интегрирующей RС-цепи с 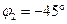 , соединенных в виде шестиполюсника (рис. 6.6). Фазовый сдвиг между
, соединенных в виде шестиполюсника (рис. 6.6). Фазовый сдвиг между  и
и  равен в этом случае 90° и поддерживается постоянным в широком диапазоне частот. Это достоинство квадратурного ФВ является в ряде случаев принципиальным и используется при проектировании ИФВ в виде фазоразностных RС-цепей, являющихся обобщением шестиполюсника, изображенного на рис. 6.6, на произвольные значения
равен в этом случае 90° и поддерживается постоянным в широком диапазоне частот. Это достоинство квадратурного ФВ является в ряде случаев принципиальным и используется при проектировании ИФВ в виде фазоразностных RС-цепей, являющихся обобщением шестиполюсника, изображенного на рис. 6.6, на произвольные значения  и
и  . Однако чаще плавное изменение
. Однако чаще плавное изменение  в широких пределах при
в широких пределах при  достигается с помощью мостовых ФВ. Типовая схема мостового ФВ и векторная диаграмма напряжений, поясняющая работу схемы, приведены на рис. 6.7.
достигается с помощью мостовых ФВ. Типовая схема мостового ФВ и векторная диаграмма напряжений, поясняющая работу схемы, приведены на рис. 6.7.
 в амплитуду результирующего (суммарного или разностного) напряжения с последующим измерением этого напряжения аналоговым или цифровым вольтметром. Таким образом, фазовые измерения трансформируются в амплитудные, существенно расширяя функции вольтметров и превращая их в амплифазометры.
в амплитуду результирующего (суммарного или разностного) напряжения с последующим измерением этого напряжения аналоговым или цифровым вольтметром. Таким образом, фазовые измерения трансформируются в амплитудные, существенно расширяя функции вольтметров и превращая их в амплифазометры.

 (6.7)
(6.7) (6.8)
(6.8) , или
, или  .Однако такой фазометр будет иметь неравномерную шкалу и резко выраженную зависимость погрешности измерения
.Однако такой фазометр будет иметь неравномерную шкалу и резко выраженную зависимость погрешности измерения  (хотя эта информация необходима для реализации амплифазометра). Поэтому в практических схемах фазометров (рис. 6.1) осуществляют дополнительные преобразования, используя для этой цели и суммарное, и разностное напряжения.
(хотя эта информация необходима для реализации амплифазометра). Поэтому в практических схемах фазометров (рис. 6.1) осуществляют дополнительные преобразования, используя для этой цели и суммарное, и разностное напряжения. и
и  уравниваются с помощью ВУ1 и ВУ2, а дополнительные преобразования сводятся либо к делению
уравниваются с помощью ВУ1 и ВУ2, а дополнительные преобразования сводятся либо к делению 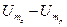 (рис. 6.1, б). В первом случае в качестве ИУ фазометра применяется ИО, рассмотренный в § 3.5.5, а во втором — дополнительная схема вычитания с вольтметром.
(рис. 6.1, б). В первом случае в качестве ИУ фазометра применяется ИО, рассмотренный в § 3.5.5, а во втором — дополнительная схема вычитания с вольтметром. (6.9)
(6.9)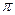 .
.
 от
от 
 пределы измерения
пределы измерения  и
и  , а в качестве измерителя
, а в качестве измерителя  чаще всего применяется ФД с магнитоэлектрическим прибором. В диапазоне СВЧ схемы сложения и вычитания представляют собой гибридные соединения типа восьми- и двенадцатиполюсников, свойства и характеристики которых рассматриваются в курсе «Антенны и устройства СВЧ». Между ними и измерительной частью фазометра включаются детекторы СВЧ сигналов, квадратичный закон детектирования которых должен учитываться при анализе работы фазометра.
чаще всего применяется ФД с магнитоэлектрическим прибором. В диапазоне СВЧ схемы сложения и вычитания представляют собой гибридные соединения типа восьми- и двенадцатиполюсников, свойства и характеристики которых рассматриваются в курсе «Антенны и устройства СВЧ». Между ними и измерительной частью фазометра включаются детекторы СВЧ сигналов, квадратичный закон детектирования которых должен учитываться при анализе работы фазометра. (6.10)
(6.10)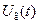 и
и  (6.11)
(6.11) и
и  — фазовые сдвиги в трактах преобразования частоты. При идентичных фазовых характеристиках этих трактов
— фазовые сдвиги в трактах преобразования частоты. При идентичных фазовых характеристиках этих трактов  и, как следует из (6.11) и (6.3), фазовый сдвиг между сигналами
и, как следует из (6.11) и (6.3), фазовый сдвиг между сигналами  и
и  по-прежнему равен
по-прежнему равен  , где
, где  — скорость изменения
— скорость изменения  . В этом случае фаза выходного сигнала ФВ
. В этом случае фаза выходного сигнала ФВ  а частота
а частота  . Если теперь преобразованный и второй сигналы подать на смеситель, то дальнейшие преобразования будут выполняться на частоте
. Если теперь преобразованный и второй сигналы подать на смеситель, то дальнейшие преобразования будут выполняться на частоте  . Этот способ позволяет избежать применения специального гетеродина, но эффективен при измерении только постоянных или медленно меняющихся
. Этот способ позволяет избежать применения специального гетеродина, но эффективен при измерении только постоянных или медленно меняющихся 
 и
и  , противофазности или квадратурности их.
, противофазности или квадратурности их. . Если
. Если  , то
, то 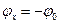 , т. е. измеряемое значение
, т. е. измеряемое значение 
 , а при
, а при 
 . Можно в принципе измерять любое промежуточное значение
. Можно в принципе измерять любое промежуточное значение  , но тогда будет реализован уже не нулевой, а дифференцированный метод измерения
, но тогда будет реализован уже не нулевой, а дифференцированный метод измерения 
 и
и 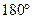 , чаще всего применяется осциллограф. При подаче
, чаще всего применяется осциллограф. При подаче  и
и 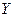 осциллографа наблюдаемая интерференционная фигура будет иметь вид эллипса, параметры которого определяются значением
осциллографа наблюдаемая интерференционная фигура будет иметь вид эллипса, параметры которого определяются значением  . Изменяя фазовый сдвиг, вносимый ФВ, фиксируют значение
. Изменяя фазовый сдвиг, вносимый ФВ, фиксируют значение 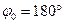 (старший разряд),
(старший разряд), 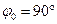 (следующий разряд) и далее с дискретом
(следующий разряд) и далее с дискретом  .
. Классификация типов ИФВ как приборов вида ФЗ достаточно обширна. В диапазоне ВЧ это RС-фазовращатели, индуктивные и емкостные, а в диапазоне СВЧ — фазовращатели на удлинителях, отражательные, диэлектрические и поляризационные. Рассмотрим в качестве примеров наиболее распространенные типы ИФВ: RC — фазовращатели, фазовращатели на удлинителях и диэлектрические ФВ.
Классификация типов ИФВ как приборов вида ФЗ достаточно обширна. В диапазоне ВЧ это RС-фазовращатели, индуктивные и емкостные, а в диапазоне СВЧ — фазовращатели на удлинителях, отражательные, диэлектрические и поляризационные. Рассмотрим в качестве примеров наиболее распространенные типы ИФВ: RC — фазовращатели, фазовращатели на удлинителях и диэлектрические ФВ. Простейшим RC-фазовращателем является элементарная RС-цепь, которая может быть дифференцирующей или интегрирующей. С помощью таких цепей можно получить изменение
Простейшим RC-фазовращателем является элементарная RС-цепь, которая может быть дифференцирующей или интегрирующей. С помощью таких цепей можно получить изменение  . Поэтому элементарные RС-цепи применяются только для создания фиксированных значений
. Поэтому элементарные RС-цепи применяются только для создания фиксированных значений 
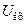 , а с другой диагонали снимается
, а с другой диагонали снимается 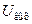 . Если
. Если  то делитель
то делитель 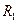 ,
,  делит
делит  является центром окружности, построенной на
является центром окружности, построенной на  и
и  также должна быть равна
также должна быть равна 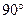 , то точка
, то точка  должна двигаться по этой окружности при изменении
должна двигаться по этой окружности при изменении  . В результате
. В результате  , а по фазе сдвинуто относительно
, а по фазе сдвинуто относительно 
 . Такие ФВ особенно удобны при реализации ИФВ с дискретным поразрядным изменением
. Такие ФВ особенно удобны при реализации ИФВ с дискретным поразрядным изменением 
 линии передачи СВЧ сигнала. Как известно из теории длинных линий, фаза бегущей волны на выходе линии определяется величиной
линии передачи СВЧ сигнала. Как известно из теории длинных линий, фаза бегущей волны на выходе линии определяется величиной 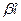 , где
, где  (для коаксиалов) или
(для коаксиалов) или  (для волноводов) - фазовая постоянная. Таким образом, изменяя
(для волноводов) - фазовая постоянная. Таким образом, изменяя  , можно получить ФВ с пределами изменения
, можно получить ФВ с пределами изменения  . Практическое применение находят две конструктивные разновидности таких ФВ: телескопический и тромбонный, схематически показанные в волноводном варианте на рис. 6.8.
. Практическое применение находят две конструктивные разновидности таких ФВ: телескопический и тромбонный, схематически показанные в волноводном варианте на рис. 6.8. . Характерные примеры диэлектрических ФВ на прямоугольном и круглом волноводах показаны на рис. 6.9.
. Характерные примеры диэлектрических ФВ на прямоугольном и круглом волноводах показаны на рис. 6.9.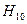 , то максимальный эффект будет получен при размещении диэлектрика в виде пластины посредине широкой стенки волновода (в пучности электрического поля). Конструктивно это можно реализовать с помощью пластинчатого (рис. 6.9, а) или ножевого (рис. 6.9, б) ФВ. Каждый из них имеет свои достоинства и недостатки, но в целом они уступают ФВ на круглом волноводе (рис. 6.9, в). При распространении в нем волны
, то максимальный эффект будет получен при размещении диэлектрика в виде пластины посредине широкой стенки волновода (в пучности электрического поля). Конструктивно это можно реализовать с помощью пластинчатого (рис. 6.9, а) или ножевого (рис. 6.9, б) ФВ. Каждый из них имеет свои достоинства и недостатки, но в целом они уступают ФВ на круглом волноводе (рис. 6.9, в). При распространении в нем волны 
 . С помощью переходов такой ФВ может быть включен в линию передачи любой конструкции.
. С помощью переходов такой ФВ может быть включен в линию передачи любой конструкции.
 очень эффективно при построении ЦИП. Широко применяется этот метод и в фазометрии, являясь основным при проектировании большинства типов ЦФ. Суть метода поясняется рис. 6.10.
очень эффективно при построении ЦИП. Широко применяется этот метод и в фазометрии, являясь основным при проектировании большинства типов ЦФ. Суть метода поясняется рис. 6.10. и
и 
 (6.12)
(6.12) . Наиболее просто это можно осуществить, если значение
. Наиболее просто это можно осуществить, если значение  , предусматривается образование из
, предусматривается образование из 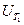 на рис. 6.10, г — это выходное напряжение преобразователя, структурная схема которого показана на рис. 6.11, а.
на рис. 6.10, г — это выходное напряжение преобразователя, структурная схема которого показана на рис. 6.11, а.
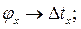
 , и
, и  ; б — короткие импульсы, соответствующие моментам перехода
; б — короткие импульсы, соответствующие моментам перехода 
 (или даже его часть) — неинтегрирующие ЦФ и измеряющие среднее за интервал времени
(или даже его часть) — неинтегрирующие ЦФ и измеряющие среднее за интервал времени  (см. рис. 6.10, г) значение
(см. рис. 6.10, г) значение 
 (6.13)
(6.13) — период следования импульсов ГСчИ. При втором измерении
— период следования импульсов ГСчИ. При втором измерении 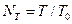 и для вычисления
и для вычисления 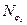 и
и 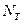 будет справедлива формула
будет справедлива формула (6.14)
(6.14)
 (n=1, 2, 3, …), то мы получаем прямоотсчетный ЦФ.
(n=1, 2, 3, …), то мы получаем прямоотсчетный ЦФ.
 и увеличением времени измерения
и увеличением времени измерения  раз (хотя измерения по-прежнему производятся за один период).
раз (хотя измерения по-прежнему производятся за один период). , через
, через  .Как видно из рис. 6.10, г,
.Как видно из рис. 6.10, г, 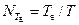 , и счетчик ИЦФ зафиксирует с учетом (6.13) общее число импульсов
, и счетчик ИЦФ зафиксирует с учетом (6.13) общее число импульсов (6.15)
(6.15) , то мы получаем прямоотсчетный фазометр. Рассмотрим возможные схемные решения ИЦФ.
, то мы получаем прямоотсчетный фазометр. Рассмотрим возможные схемные решения ИЦФ.
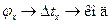 . На выходе селектора 1 образуются пачки счетных импульсов, причем число импульсов в одной пачке равно
. На выходе селектора 1 образуются пачки счетных импульсов, причем число импульсов в одной пачке равно 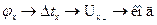 . На возможность такой реализации было указано при характеристике самого метода преобразования
. На возможность такой реализации было указано при характеристике самого метода преобразования 


