
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приборов для измерения фазового сдвигаСодержание книги
Поиск на нашем сайте
Под фазой гармонического сигнала понимается аргумент функции
где Um, ω и θ — постоянные амплитуда, угловая частота и начальная фаза сигнала. Таким образом, фаза сигнала Ψ=ωt+θ является линейной функцией времени и может изменяться при -∞<t<∞ в сколь угодно широких пределах. Однако в силу периодичности (6.1) можно ограничить пределы изменения Ψзначениями 0 - 2π или ± π. Измерение Ψ практического интереса не представляет, поскольку фактически полную информацию о гармоническом сигнале дают результаты измерений Um и f (или T). Другое дело, если мы имеем два или несколько взаимосвязанных гармонических сигналов одинаковой частоты. Если, например,
то разность фаз Ψ1 – Ψ2= θ1 - θ2 является постоянной величиной и может однозначно характеризовать степень взаимосвязи Ut(t) и U2(t). В частности, если θ1 - θ2 = 0, то такие сигналы будут синфазными. При практическом применении (Ψ1 – Ψ2) в качестве характеристики взаимосвязи сигналов достаточно часто знать только модуль
опуская информацию о знаке (Ψ1 – Ψ2). В связи с этим величина φ получила название фазового сдвига и чаще всего является целью фазовых измерений, хотя фазометры позволяют, как правило, определять и знак (Ψ1 – Ψ2). Поскольку фазовые параметры имеют ясный физический смысл для гармонических сигналов, гармонический анализ периодических сигналов сложной формы также может проводиться с их помощью. В этом случае фазовый сдвиг является мерой взаимосвязи гармоник, которые образуют спектр сигнала сложной формы. Покажем это на примере сигналов с кратными частотами nω и kω:
Если в процессе измерений, проводимых, например, на частоте
и из (6.4) получаем
т. е. по-прежнему
Как и частотно-временные измерения, фазовые измерения можно классифицировать на абсолютные и относительные. Задачей абсолютных измерений является определение
Как уже подчеркивалось, фазовыми параметрами характеризуются не только электрические сигналы, но и электрорадиотехнические цепи. Для двухполюсников важно знать фазовый сдвиг между током и напряжением (в случае цепей с сосредоточенными постоянными) или фазу коэффициента отражения (при переходе к цепям с распределенными постоянными). Четырехполюсники (ЧП) характеризуются модулем и фазой коэффициента передачи, причем зависимость Фазометры входят в подгруппу Ф (см. § 2.1), образуя вид Ф2. Самостоятельный вид ФЗ составляют измерительные фазовращатели — образцовые меры Хотя фазометры не подразделяются на виды в зависимости от конкретного назначения или принципа работы, это вовсе не означает, что принцип работы всех фазометров базируется на каком-то одном методе измерения
|
|||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.236 (0.009 с.) |

 (6.1)
(6.1) (6.2)
(6.2) , (6.3)
, (6.3) (6.4)
(6.4) , умножить частоту сигнала
, умножить частоту сигнала  в
в 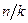 раз, то тогда
раз, то тогда
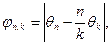 (6.5)
(6.5) не зависит от t и может являться мерой взаимосвязи Un(t) и Uk (t). Если выбрать n = 1, то тогда фазовые сдвиги гармоник будут измеряться относительно первой гармоники и в соответствии с (6.5)
не зависит от t и может являться мерой взаимосвязи Un(t) и Uk (t). Если выбрать n = 1, то тогда фазовые сдвиги гармоник будут измеряться относительно первой гармоники и в соответствии с (6.5) (6.6)
(6.6) , а задачей относительных измерений — определение изменений
, а задачей относительных измерений — определение изменений  и
и  в (6.2). Измерение флюктуации фазы относится к измерениям характеристик случайных сигналов.
в (6.2). Измерение флюктуации фазы относится к измерениям характеристик случайных сигналов. является ФЧХ четырехполюсника.
является ФЧХ четырехполюсника.


