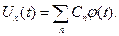Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения и классификация анализаторов спектраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В основе спектральных методов анализа лежит, как известно, преобразование Фурье для временной функции, описывающей исследуемый сигнал. Если сигнал является периодическим, он может быть представлен суммой гармонических составляющих, описываемых рядом
где
В практике электрорадиоизмерений интересуются, как правило, только амплитудным спектром (называя его просто спектром) и при экспериментальном анализе воспроизводят в координатах Как видно из (7.7), спектры периодических сигналов являются дискретными и образуются равноотстоящими спектральными линиями (гармониками) с частотным интервалом между соседними линиями, определяемым периодом повторения сигнала Тх. Форма огибающей спектра целиком определяется формой сигнала и не зависит от Тх. При увеличении Тх спектральные линии сближаются и в предельном случае
где
откуда для амплитудного спектра непериодического сигнала
а для фазового сдвига
Выражение (7.8) является так называемым обратным преобразованием Фурье, позволяющим по известным
откуда
В качестве примеров приведены амплитудный и фазовый спектры одиночных видеоимпульса (рис. 7.27, а) и радиоимпульса (рис. 7.27, б) прямоугольной формы. В силу бесконечности спектров периодических и непериодических сигналов при экспериментальном анализе их ограничиваются определением ширины спектра, под которой понимают интервал частот, где сосредоточена основная часть энергии сигнала. Как видно из рис. 7.27, для видео- и радиоимпульсов прямоугольной формы основная часть энергии сосредоточена
Рис. 7.27. Спектры одиночных импульсов.
в главном лепестке. В АС обеспечивается возможность воспроизведения по крайней мере еще двух боковых лепестков спектра. Однако и в этом случае экспериментальный анализ спектра ограничен во времени. Вместо, например, комплексного спектра (7.9) или его составляющих (7.10) мы можем определить только так называемый аппаратурный спектр Кроме ряда Фурье (7.7), базирующегося на системе тригонометрических функций, спектральное разложение периодических сигналов может быть произведено по функциям Уолша и Хаара. Поэтому в общем случае необходимо иметь в виду возможность представления периодического сигнала в виде ряда некоторой полной системы ортогональных функций
Анализаторы спектра принято классифицировать в соответствии с методом анализа спектра и способом проведения анализа. В зависимости от метода анализа выделяют фильтровые АС, реализующие метод фильтрации, дисперсионные АС, базирующиеся на дисперсионно-временном методе анализа, рециркуляционные АС, реализующие так называемый рециркуляционный (интерференционный) метод, и цифровые АС, использующие алгоритмы дискретного преобразования Фурье. По способу проведения анализа спектра различают АС параллельного и последовательного действия, а также комбинированные АС. Охарактеризуем кратко эти способы. Параллельный анализ спектра позволяет выявить и проанализировать все составляющие спектра одновременно. Такой анализ производится без потери информации в реальном масштабе времени и эффективен как для периодических, так и для непериодических сигналов. Однако в аппаратурном отношении АС параллельного действия — это сложные, а иногда и трудно реализуемые приборы. При последовательном анализе составляющие спектра выявляются и анализируются последовательно (поочередно). Это имеет практический смысл лишь при неизменном в течение
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.214.4 (0.037 с.) |

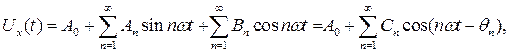 (7.7)
(7.7)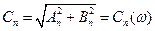 - амплитудный спектр, а
- амплитудный спектр, а  - фазовый спектр сигнала.
- фазовый спектр сигнала.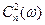 - энергетический спектр. Однако при решении целого ряда задач (например, восстановление сигнала по известным
- энергетический спектр. Однако при решении целого ряда задач (например, восстановление сигнала по известным 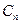 и
и 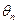 ) необходимо определять как амплитудный, так и фазовый спектры.
) необходимо определять как амплитудный, так и фазовый спектры. образуют сплошной спектр. Этот случай соответствует непериодическому сигналу, для определения которого необходимо перейти от ряда Фурье (7.7) к интегралу Фурье
образуют сплошной спектр. Этот случай соответствует непериодическому сигналу, для определения которого необходимо перейти от ряда Фурье (7.7) к интегралу Фурье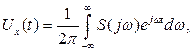 (7.8)
(7.8)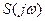 называется комплексным спектром
называется комплексным спектром 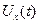 и может быть представлен как
и может быть представлен как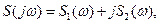
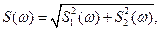
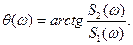
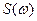 и
и 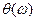 или
или 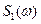 и
и 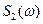 восстановить исследуемый сигнал. Для определения
восстановить исследуемый сигнал. Для определения 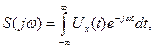 (7.9)
(7.9) (7.10)
(7.10)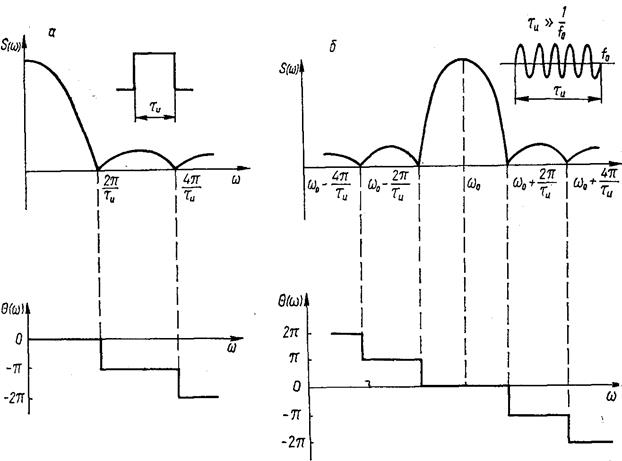
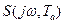 и его составляющие
и его составляющие  и
и  , получаемые заменой в (7.9) и (7.10) пределов интегрирования с
, получаемые заменой в (7.9) и (7.10) пределов интегрирования с  на
на  , где
, где  — время анализа. Таким образом, аппаратурный спектр — функция не только частоты, но и времени анализа и поэтому получил название текущего спектра. Конечность (финитность)
— время анализа. Таким образом, аппаратурный спектр — функция не только частоты, но и времени анализа и поэтому получил название текущего спектра. Конечность (финитность)