Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектр Фур'є неперервних та дискретних сигналів.Содержание книги
Поиск на нашем сайте
Нехай
де У свою чергу Фур'є-спектр
Співвідношення (1.1), (1.2) являють собою пари інтегральних перетворень Фур'є, причому (1.2) – пряме перетворення Фур'є, (1.1) – іобернене перетворення Фур'є. Відмітимо, що сигнал Основні властивості Фур'є-спектра 1. Функція
Функцію 2. Внаслідок дійсності сигналу
3. Енергія спектра Фур'є обмежена й дорівнює енергії вихідного сигналу (рівність Парсеваля):
У теорії безперервних лінійних систем з постійними параметрами широко використовується поняття перетворення Лапласа (s - перетворення):
функції, визначеної на комплексної s- площині: При цьому пряме перетворення Фур'є (1.2) може розглядатися як перетворення Лапласа, обчислене на уявній осі в s-площині:
У зв'язку із цим, у літературі часто можна зустріти позначення для Фур'є-спектра – В теорії дискретних лінійних систем замість s-перетворення Лапласа широко використовується поняття Z-перетворення дискретного сигналу
Z-перетворення має сенс, для тих значень комплексної змінної z, при яких ряд (1.4) збігається. Z-перетворення лінійне, завдяки чому воно успішно використовується при описі лінійних дискретних систем. Вихідна послідовність може бути відновлена за допомогою оберненого Z - перетворення:
де С – замкнутий контур, що охоплює все особливі точки функції Спектр Фур'є дискретних сигналів. Спектром Фур'є послідовності
Вираз (1.6) показує, як вихідна послідовність може бути зібрана з дискретизованих комплексних синусоїд різних частот, узятих з вагами
Z - перетворення. Ефективність частотного аналізу дискретних сигналів істотно зростає, якщо замінити перетворення Лапласа Z - перетворенням. У цьому випадку зображення сигналу X (p), яке представляє собою трансцендентну функцію змінної P = d + jw, замінюється Z - зображенням сигналу X (Z), яке є раціональною функцією змінної Z = x + jy. Формули Z - перетворення виходять з формули Лапласа (1.6) заміною змінних epT = Z. (1.7) Підстановка (1.7) та її похідної dZ / dp = TepT в (1.6) приводить до формул прямого і зворотного Z - перетворення
Точки на уявної осі комплексного змінного p = d + jw, тобто точки p = jw, визначають реально частотні характеристики сигналу. Уявної осі відповідає на площині Z одиничне коло, тому що в цьому випадку згідно (1.7) Z = ejwT = Тому безперервного росту змінної на уявної осі площині p = d + jw, відповідає багаторазовий обхід одиничному колі на площині z = x + jy (Мал. 1.4). Цим фактом пояснюється, зокрема, та обставина, що інтегрування у формулі зворотного z - перетворення (1.8) здійснюється уздовж одиничному колі площині z замість інтегрування уздовж прямої паралельної уявної площини p. Враховуючи вищевикладене та формули (1.7), (1.9) можна стверджувати, що ліва полуплоскость змінного p = d + jw відображається на площину одиничного кола змінного z = x + jy, права полуплоскость - на площину z за межами одиничного кола.
Підстановка (1.9) в z - зображення сигналу призводить до спектру цього сигналу, підстановка (1.7) дає зображення по Лапласа. Приклад. Визначити спектр та побудувати графіки модуля й аргументу спектральної щільності сигналу x (nT) = {a; b} (Мал. 1.5, а).
Рішення. Z - зображення сигналу згідно (1.8) X (Z) = Звідси підстановкою (1.9) визначаємо спектр сигналу X (jw) = a + be-jwT. Графіки модуля й аргументу спектральної щільності наведені на малюнку 1.6, а, б на інтервалі частот [0; wд].
Поза інтервалу частот [0; wд] частотні залежності повторюються з періодом wд.
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.87 (0.011 с.) |

 – неперервний сигнал, що задовольняє умові
– неперервний сигнал, що задовольняє умові  . Сигнал
. Сигнал  . (1.1)
. (1.1) – комплексна функція, що визначає амплітуду та фазову затримку комплексної синусоїди із частотою
– комплексна функція, що визначає амплітуду та фазову затримку комплексної синусоїди із частотою  :
:  . У загальному випадку ця функція визначена на всій осі частот
. У загальному випадку ця функція визначена на всій осі частот  і називається вона Фур'є-спектром сигналу
і називається вона Фур'є-спектром сигналу  (1.2)
(1.2) и Фур'є-спектр
и Фур'є-спектр  .
. називають амплітудним спектром (іноді магнітудою спектра), вона визначає дійсну амплітуду синусоїди із частотою
називають амплітудним спектром (іноді магнітудою спектра), вона визначає дійсну амплітуду синусоїди із частотою  , що приймає участь у формуванні сигналу. Функцію
, що приймає участь у формуванні сигналу. Функцію  називають фазовим спектром, вона показує фазовий зсув, якому варто піддати комплексну синусоїду частоти
називають фазовим спектром, вона показує фазовий зсув, якому варто піддати комплексну синусоїду частоти 
 ,
, 
 ,
, 

 , (1.3)
, (1.3) .
. .
. , в якому є вказівка на те, що це спектр саме неперервного сигналу.
, в якому є вказівка на те, що це спектр саме неперервного сигналу. (1.4)
(1.4) ,
, .
. називають комплексну функцію
називають комплексну функцію 
 (1.5)
(1.5) (1.6)
(1.6) . Порівняння (1.5) з (1.4) показує, що спектр Фур'є
. Порівняння (1.5) з (1.4) показує, що спектр Фур'є  в комплексній Z-площині. Властивості спектра Фур'є дискретних сигналів подібні до властивостей спектра Фур'є неперервних сигналів. Однак є принципова відмінність. Спектр
в комплексній Z-площині. Властивості спектра Фур'є дискретних сигналів подібні до властивостей спектра Фур'є неперервних сигналів. Однак є принципова відмінність. Спектр  . Тому його значення розглядають на одному періоді – або
. Тому його значення розглядають на одному періоді – або  , або
, або  .
. (1.8)
(1.8) (1.9)
(1.9)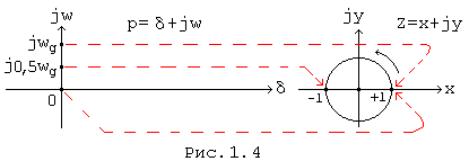
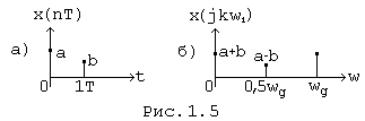
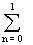 x (nT) Zn = x (0T) Z-0 + x (1T) Z-1 = a + bZ-1
x (nT) Zn = x (0T) Z-0 + x (1T) Z-1 = a + bZ-1