
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості лінійних дискретних системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Раніше було відзначено, що всі стаціонарні лінійні системи (аналогові і дискретні) мають загальні властивості: - Адитивності; - Однорідності; - Інваріантності у часі. Розглянемо ще два найважливіші властивості лінійних дискретних систем: - Властивість пам'яті; - Стійкість. Властивість пам'яті лінійних дискретних систем Властивість пам'яті системи передбачає її здатність "пам'ятати передісторію" (попередні відліки впливу) при обчисленні реакції в поточний момент часу. Тривалість передісторії (кількість попередніх відліків впливу) визначає тривалість пам'яті. Розглянемо властивість пам'яті нерекурсивних і рекурсивних ЛДС. Згідно різницевого рівняння нерекурсивною ЛДС (4.21). при обчисленні реакції y(n) в поточний n -ий момент часу система «пам'ятає» (N-1), що передують відліків впливу. Отже, нерекурсивна ЛДС має властивість пам'яті, її тривалість кінечна і дорівнює (N-1). Згідно різницевого рівняння рекурсивної ЛДС (4.14), кожен поточний відлік реакції y(n) можна виразити через попередні відліки впливу:
Таким чином: □ відлік реакції у (0) залежить від поточного відліку впливу x (0); □ відлік в y(1) залежить від поточного і попереднього відліків впливу x(1-i), i=0,1; □ відлік у (2) залежить від поточного та двох попередніх відліків впливу x(2-i), i = 0,1, 2. Аналогічним чином, нескладно показати, що відлік y (3) залежить від відліків впливу x(3-i), i = 0,1, 2,3 і т. д. Отже, при обчисленні відліку реакції в поточний л-й момент часу система «пам'ятає» всю передісторію впливу, а значить, рекурсивна ЛДС має властивість пам'яті та її тривалість в загальному випадку бесконеч на. Це властивість пам'яті рекурсивних ЛДС пояснюється наявністю зворотного зв'язку (див. формулу (4.14)), завдяки чому будь-який ненульовий відлік впливу циркулює в системі нескінченно. З плином часу він затухає, але присутній, але принаймні, теоретично. Стійкість лінійних дискретних систем ЛДС називається стійкою, якщо при обмеженому впливі
де
де Існують два критерії стійкості ЛДС. Один з них дозволяє оцінити стійкість ЛДС за її характеристиці в часовій області, інший - по z -зображенню цієї характеристики в пана області.
Оцінка стійкості по імпульсної характеристиці: критерій стійкості Якщо жоден з коефіцієнтів розкладання імпульсної характеристики у вигляді (3.45)
не дорівнює нулю:
критерій стійкості формулюється так: для того щоб лінійна дискретна система була стійка, необхідно і достатньо, щоб виконувалася умова абсолютної збіжності ряду
Доказ. При відомої імпульсної характеристиці h(n) реакція може бути обчислена але формулою згортки (4.9)
Для мо.дуля реакції справедливі співвідношення:
Оцінимо максимальне значення (4.26) Якщо реакція обмежена значеніечі
необхідно, щоб виконувалася умова (4.25). З іншого боку, для того щоб реакція в (4.26) була обмеженою, досить виконання умови (4.25), що й було потрібно довести. Якщо хоча б один з коефіцієнтів розкладання Критерій (4.25) дозволяє стверджувати, що нерекурсівние ЛДС (КИХ-системи) принципово стійкі, оскільки їх імпульсна характеристика кінцева. Перш ніж робити висновки про стійкість рекурсивних ЛДС, розглянемо простої приклад. Приклад Визначити, стійка чи рекурсивна ЛДС, імпульсна характеристика (IX) якої має вид дискретної експоненти
Рішення. Підставивши дану IХ в (4.25), отримаємо ряд типу (3.20)
при q= У цій області імпульсна характеристика має вигляд затухаючої експоненти, а ЛДС, згідно критерію (4.25), є стійкою. Поза області збіжності, при | a |
а ЛДС, згідно критерію (4.25), нестійкою.
Узагальнюючи даний результат, можна зробити наступні висновки: - Рекурсивні ЛДС (БИХ-системи) вимагають перевірки на стійкість; - Імпульсна характеристика стійкою рекурсивної ЛДС має характер затухаючої функції часу.
|
|||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.148 (0.008 с.) |

 ;
; ;
; ;
; - будь-яке як завгодно велике позитивне число, не рівне нескінченності, і довільних, але обмежених початкових умовах реакція буде також обмеженою
- будь-яке як завгодно велике позитивне число, не рівне нескінченності, і довільних, але обмежених початкових умовах реакція буде також обмеженою - будь-яке як завгодно велике позитивне число, не рівне без-кінцівки.
- будь-яке як завгодно велике позитивне число, не рівне без-кінцівки.
 ,
, (4.25)
(4.25)

 , підставивши замість відліків впливу
, підставивши замість відліків впливу  їх максимально допустиму величину
їх максимально допустиму величину  дорівнює нулю, можлива ситуація, коли умова (4.25) виконується, а ЛДС-нестійка.
дорівнює нулю, можлива ситуація, коли умова (4.25) виконується, а ЛДС-нестійка.
 (4.27)
(4.27) область його збіжності
область його збіжності 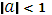 .
.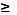 1, ряд (4.27) виявляється розбіжним
1, ряд (4.27) виявляється розбіжним



