
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричне подання циклічних кодівСодержание книги
Поиск на нашем сайте
Для формування рядків породжувальної матриці за першим способом утворення циклічного коду беруть комбінації простого k-розрядного коду G(х), що містять одиницю в одному розряді. Ці комбінації збільшуються на хn-k, визначається залишок R(х) від ділення отриманого добутку хn-kG(х) на утворюючий поліном і записується відповідний рядок матриці у вигляді суми добутку хn-kG(х) і залишку R(х). При цьому породжувальна матриця Рn,k подається двома підматрицями – інформаційною Uk і додатковою Нр:
Інформаційна підматриця Uk, являє собою квадратну одиничну матрицю з кількістю рядків і стовпців, рівною k. Додаткова підматриця Нр містить р = п - k стовпців і k рядків і утворена залишками R(х). Породжувальна матриця дозволяє одержати k комбінацій коду. Інші комбінації утворюються підсумовуванням за модулем два рядків породжувальної матриці у всіх можливих поєднаннях. При другому способі утворення циклічного коду породжувальна матриця Pn,k формується шляхом множення утворюючого полінома Р(х) степеня Вибір утворюючого полінома При побудові циклічного коду спочатку визначається число інформаційних розрядів k за заданим об’ємом коду. Потім знаходиться найменша довжина кодових комбінацій n, що забезпечує виявлення або виправлення помилок заданої кратності. Ця проблема зводиться до перебування потрібного утворюючого полінома Р(х). Як уже відзначалося раніше, степінь утворюючого полінома повинен дорівнювати числу перевірних розрядів Оскільки в циклічному коді розпізнювачами помилок є залишки від ділення многочлена прийнятої комбінації на утворюючий коректувальний многочлен, то спроможність коду буде тим вища, чим більше залишків може бути утворено в результаті цього ділення. Найбільше число залишків, що дорівнює 2-1 (крім нульового), може забезпечити тільки многочлен порядка степеня Відомо, що двочлен типу (хn + 1) = (х2z-1 + 1), у розкладанні якого як співмножник повинен входити утворюючий многочлен, має ту властивість, що він є спільним кратним для усіх без винятку незвідних поліномів степеня n і розкладається на множники з усіх незвідних поліномів степеня 2, які діляться без залишку на число z.
Найпростішим циклічним кодом є код, що забезпечує виявлення однократних помилок. Вектору однократної помилки відповідає одночлен xi, степінь котрого i може приймати значення від 1 до п. Для того щоб могла бути виявлена помилка, одночлен xi не повинен ділитися на утворюючий поліном Р(х). Серед незвідних многочленів, що входять у розкладання двочлена хn + 1, є багаточлен найменшого степеня х + 1. Таким чином утворюючим поліномом даного коду є двочлен Р(х) = х + 1. Залишок від ділення будь-якого многочлена на х + 1 може приймати тільки два значення: 0 і 1. Отже, при будь-якому числі інформаційних розрядів необхідний тільки один перевірний розряд. Значення символу цього розряду забезпечує парність числа одиниць у кодовій комбінації. Даний циклічний код із перевіркою на парність забезпечує виявлення не тільки однократних помилок, але і всіх помилок непарної кратності. Для побудови циклічного коду, що виправляє однократні або виявляє дворазові помилки, необхідно, щоб кожній одиничній помилці відповідав свій розпізнавач, тобто залишок від ділення многочлена прийнятої комбінації на утворюючий многочлен. Оскільки кількість можливих однократних помилок дорівнює п, а незвідний многочлен степеня
Звідси знаходять степінь утворюючого полінома
і загальну довжину п кодової комбінації. Оскільки утворюючий многочлен Р(х) повинен входити як співмножник в розкладання двочлена (хn + 1) = (х2z-1 + 1), то використовуючи відзначені раніше властивості цього двочлена, а також умову (5.6), можна вибрати утворюючий поліном. Однак не всякий мнгочлен степеня Утворюючі поліноми кодів, які здатні виправляти помилки будь-якої кратності, можна визначати, користуючись таким правилом Хеммінга.
1. За заданим числом інформаційних розрядів k визначається число перевірних розрядів 2. Розглядаючи отриманий (n, k)-код і некоректуючий n-розрядний код визначають додаткові розряди для забезпечення виправлення однієї помилки в цьому коді і знаходять відповідний утворюючий поліном. 3. Повторюється дана процедура стільки разів, поки не буде отриманий код, що виправляє незалежні помилки до даної кратності включно. Закодувати просту інформаційну групу G(х) = 1011 циклічним кодом, що забезпечує виявлення дворазових або усунення однократних помилок. Розв’язання. За заданою кількістю інформаційних символів k = 4
визначаємо значність коду. Користуючись співвідношенням (5.6) і табл. 5.1, отримаємо n = 3,2. Для побудови циклічного коду необхідно вибрати утворюючий поліном Р(х) степеня
Вибираємо як утворюючий поліном співмножник
Кодування здійснюємо першим способом. Для цього вихідну кодову комбінацію G(х) множимо на xn-k=x3
Визначаємо залишок R(х) від розподілу хn-k G(х) на утворюючий багаточлен Р(х):
Залишок R(x) = х2. Отже, поліном F(х) циклічного коду буде мати вигляд
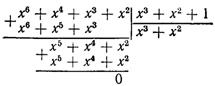
Отримане повідомлення циклічним кодом Р*(х) = х6+ х4 + х3 + х2. Перевірити декодуванням наявність помилок у прийнятій комбінації, якщо утворюючий поліном Р(х) == х3 + х2 +1. Розв’язання. Декодування здійснюється діленням полінома отриманої комбінації на утворюючий поліном
Залишок від розподілу R(х) = 0. Отже, комбінація прийнята без перекручувань.
Отримана комбінація P*(х) = х6 + х4 + х2 + 1, закодована циклічним кодом. Утворюючий поліном Р(х) = х3 + х2 + 1. Перевірити наявність помилок у кодовій комбінації. Розв’язання. Ділимо поліном отриманої комбінації на утворюючий поліном
залишок – R(х) = х2 0. Отже, комбінація прийнята з помилками. Побудувати породжувальну матрицю циклічного коду при n = 7; Розв’язання. Оскільки k = 4, інформаційна підматриця має вигляд
Для одержання першого рядка додаткової підматриці множимо перший рядок інформаційної підматриці на x3. Ділимо на утворюючий поліном, тобто виконуємо операції
Остаточно одержимо таку породжувальну матрицю:
Для побудови породжувальної матриці другим способом перший рядок матриці одержуємо шляхом множення утворюючого полінома на
Згорткові коди. Згорткові коди відносяться до безперервних рекурентних кодів. Кодове слово є згорткою відгуку лінійної системи (кодера) на вхідну інформаційну послідовність. Тому згорткові коди є лінійними, для яких сума будь-яких кодових слів також є кодовою послідовністю.
Розглянемо згортковий код з швидкостями вигляду Кодер загорткового коду містить тактований регістр памяті для збереження визначеного числа інформаційних символів і перетворювач вхідної інформаційної послідовності у вихідну кодову послідовність. Структурна схема кодера ЗК (7.5) зображена на рисунку 1.3.
Рис.1.3 – Структурна схема кодера
Послідовність кодування детально розписана в таблиці 1. Таблиця 1 - Процес кодування послідовності інформаційних бітів 01101000
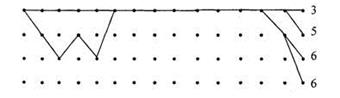
Способи задання згорткових кодів багато в чому збігаються з використовуваними для лінійних блокових. Одним з основних є опис згорткового коду набором Кодові грати цього коду показані на мал. 1.1. При його складанні враховано, що кодер містить пам'ять у вигляді дворозрядного регістра. Кожному з чотирьох можливих станів цього регістра відповідає один з чотирьох вузлів решітки. Тому лівий символ в позначенні вузла дорівнює останньому інформаційному біту, вже записаному в регістр. При записі в регістр чергового інформаційного символу регістр міняє стан на одне з двох сусідніх. Цей перехід позначений ребрами грат. Порядок вузлів вибраний таким, що при нульовому поточному інформаційному символі (а=0) перехід в наступний стан відповідає верхньому ребру, а при
Рисунок 1.1 - Кодові грати
Кожній інформаційній послідовності відповідає певний шлях на кодових гратах і кодова послідовність. Наприклад, вхідним інформаційним бітам 01100 відповідає кодове слово 00 11 01 01 11, якому відповідає на мал. 1.1 шлях, відмічений жирною лінією. Відомий ряд алгоритмів декодування згортальних кодів. У практичних системах і, зокрема в мобільному зв'язку, як правило, використовується алгоритм Вітербі, що відрізняється простотою реалізації при помірних довжинах кодового обмеження.
Алгоритм Вітербі реалізує оптимальне (максимально правдоподібне) декодування як рекурентний пошук на кодовой гратах шляху, найближчого до послідовності, що приймається. На кожній ітерації алгоритму Вітербі зіставляються два шляхи, що ведуть в даний стан (вузол грат). Найближчий з них до прийнятої послідовності зберігається для подальшого аналізу. Нехай передається нульове кодове слово, а в каналі виникла трикратна помилка, так що прийнята послідовність має вигляд 10 10 00 00 10 00... 00.... Результати пошуку найближчої дороги після прийому 14 елементарних блоків показані на рисунку 1.2.
Рисунок 1.2 - Приклад роботи алгоритму Вітербі
Імпульсно-кодова модуляція І́мпульсно-ко́дова модуля́ція ---- використовується для оцифровки аналогових сигналів перед їхньою передачею. Практично всі види аналогових даних (відео, голос, музика, дані телеметрії, віртуальні мири) допускають застосування імпульсно-кодовій модуляції.
Щоб одержати на вході каналу зв'язку (передавальний кінець) ІК-модульований сигнал з аналогового, амплітуда аналогового сигналу вимірюється через рівні проміжки часу. Кількість оцифрованих значень у секунду (або швидкість оцифрування) кратна максимальній частоті (Гц) у спектрі аналогового сигналу. Миттєве обмірюване значення аналогового сигналу округляється до найближчого рівня з декількох заздалегідь певних значень. Цей процес називається квантуванням, а кількість рівнів завжди береться кратним ступеню двійки, наприклад, 8, 16, 32 або 64. Номер рівня може бути відповідно представлений 3, 4, 5 або 6 бітами. Таким чином, на виході модулятора виходить набір бітів (0 або 1).
На прийомному кінці каналу зв'язку демодулятор перетворює послідовність бітів в імпульси з тим же рівнем квантування, що використав модулятор. Далі ці імпульси використовуються для відновлення аналогового сигналу.
Різновидами ІКМ є: Диференціальна (або дельта) імпульсно-кодова модуляція (ДІКМ) кодує сигнал у вигляді різниці між поточним і попереднім значенням. Для звукових даних такий тип модуляції зменшує необхідну кількість біт на відлік приблизно на 25%. Адаптивна ДІКМ (АДІКМ) є різновидом ДІКМ, що змінює рівень кроку квантування, що дозволяє ще більше зменшити вимоги до смуги пропускання при заданому відношенні сигналу і шуму.
Импульсно-кодовая модуляция
Передача квантованных значений сигнала с помощью коротких импульсов различной высоты называется амплитудно-импульсной модуляцией (АИМ). Под импульсно-кодовой модуляцией (ИКМ) понимается передача непрерывных функций при помощи двоичного кода.
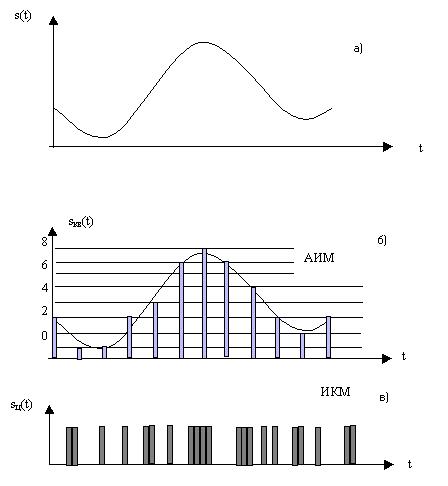
При кодовой модуляции необходимо передать числа, выражающие величину квантованных отсчетов. Для этого можно воспользоваться двоичным кодом. Числа, подлежащие передаче, надо записать в двоичной системе счисления – это и даст необходимые кодовые комбинации. При помощи n - значных двоичных чисел можно представить чисел. Благодаря квантованию количество чисел, подлежащих передаче, сводится до конечной величины. Если принять шаг квантования за единицу, то будет означать наибольшее квантованное значение. Количество знаков в двоичной кодовой комбинации равно. Если n – не целое, то оно округляется до ближайшего целого числа. На рис.3 показаны преобразования аналогового сигнала (а) в АИМ (б) и ИКМ (в) для n = 4.
Рис. 3
При выборе шага квантования (или числа N) следует учитывать два фактора. С одной стороны, увеличение числа ступеней квантования увеличивает точность передачи сигнала, с другой – требует удлинения кодовой комбинации (n). Так для телефонной передачи установлено, что удовлетворительное качество передачи достигается при
При анализе приема сигналов с импульсно-кодовой модуляцией обычно рассматривают не отношение средних мощностей сигнала и помехи, а отношение половины шага квантования
заменяет отношение сигнал – шум.
Пусть число уровней квантования равно N. Будем передавать каждое из N значений n-значным кодовым числом, составленным из импульсов, квантованных на m уровней (АИМ). Общее число возможных комбинаций равно
Если все уровни равновероятны, средняя мощность сигнала равна
Отсюда шаг квантования равен
откуда
Таким образом, при неизменных мощностях сигнала и помехи выгодно уменьшать основание кода. Наименьшее значение m равно 2 (двоичный код), что соответствует ИКМ. В этом случае
В обычной АИМ N=m >>1, и в этом случае
Следовательно, ИКМ дает выигрыш в отношении сигнал – помеха в
Какой же ценой достигается этот выигрыш? Если при АИМ за каждый тактовый интервал (отсчет) передается один импульс, то при ИКМ за тот же интервал должны быть переданы n импульсов. При неизменной скважности каждый из этих n импульсов в n раз короче (см. рис. 3), а, следовательно, ширина спектра сигнала в n раз больше, чем ширина спектра сигнала АИМ. Таким образом, за увеличение отношения сигнал – помеха мы расплачиваемся расширением полосы.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.182.15 (0.015 с.) |

 .
.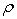 = n - k на одночлен xk-1 наступних k-1 зсувів отриманої комбінації.
= n - k на одночлен xk-1 наступних k-1 зсувів отриманої комбінації.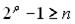 .
.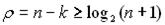 (5.6)
(5.6)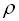 , необхідне для виправлення однократних помилок, і знаходиться утворюючий поліном.
, необхідне для виправлення однократних помилок, і знаходиться утворюючий поліном.
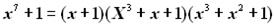 .
. .
.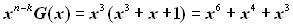 .
.
 .
.
 .
. .
.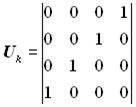 .
.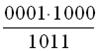 . Залишок від цих операцій 011 складає перший рядок додаткової підматриці. Аналогічно визначаємо інші рядки додаткової підматриці. Додаткова підматриця має вигляд:
. Залишок від цих операцій 011 складає перший рядок додаткової підматриці. Аналогічно визначаємо інші рядки додаткової підматриці. Додаткова підматриця має вигляд: .
.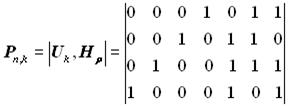 .
.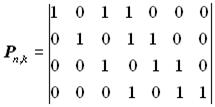 .
.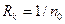 , де
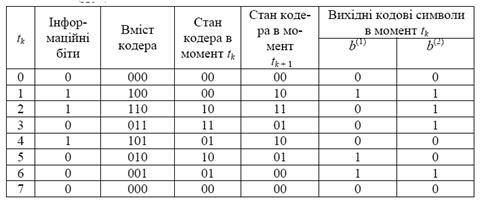
, де 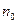 - деяке натуральне число.Послідовність символів такого згорткового коду складається з елементарних блоків завдовжки
- деяке натуральне число.Послідовність символів такого згорткового коду складається з елементарних блоків завдовжки 
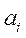 = 1 - нижньому.
= 1 - нижньому.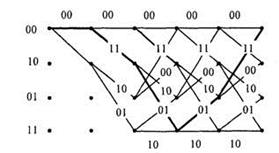

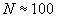 , т.е. при семизначном коде.
, т.е. при семизначном коде.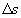 (цена округления) к среднеквадратичному значению помехи
(цена округления) к среднеквадратичному значению помехи  . Квадрат отношения
. Квадрат отношения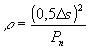
 . Очевидно, что
. Очевидно, что 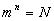 . Пусть шкала уровней симметрична относительно нуля, т. е. разрешенными являются уровни:
. Пусть шкала уровней симметрична относительно нуля, т. е. разрешенными являются уровни: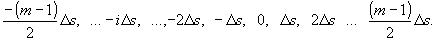
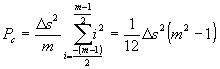
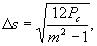
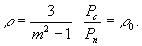
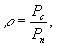 т.е. введенная величина
т.е. введенная величина 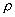 совпадает с обычным определением отношения сигнал – помеха.
совпадает с обычным определением отношения сигнал – помеха.
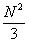 раз.
раз.


