Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ефект близькості в двопровідній лінії зв’язку. Причина явища.Содержание книги
Поиск на нашем сайте
Двухпроводная линия, представляющая собой систему двух параллельных проводов, широко используется на практике. Строгий анализ основных собственных волн в такой линии при конечной проводимости проводов был проведен на основе решения уравнения Гельмгольца в биполярной системе координат [13]. Он является весьма сложным и здесь не приводится. Ограничимся рассмотрением идеальной двухпроводной линии, т.е. будем считать, что провода обладают бесконечной проводимостью и расположены в однородной изотропной среде без потерь. В такой линии возможно распространение ТЕМ-волн двух типов, которые принято называть однотактной и, двухтактной или соответственно четной и нечетной волнами, В любом поперечном сечении линии у однотактной волны токи в проводах синфазны, а у двухтактной -противофазны (имеют противоположное направление). Ограничимся рассмотрением двухтактной волны.
Поперечное сечение линии и используемая декартова система координат показаны на рис. 10.34. Расстояние между осями проводов dh = 2, радиусы проводов одинаковы и равны а. Комплексные амплитуды токов в первом (i т 1) и втором (iт2) проводах (рис. 10.34) и векторы Ё и Н в соответствии с общей теорией ТЕМ-волн(см.9.4) представим в виде
При этом выполняется равенство Е°(х, у) =-grad u°(x, у), где функция и°(х, у) совпадает с электростатическим потенциалом в двумерной задаче о поле двух разноименно заряженных цилиндров, на одном из которых потенциал и°= V0 (первый провод), а на другом и°=- V° (второй провод). Эта задача рассматривалась в 3.6.3, и было показано, что электростатическое поле таких проводов эквивалентно полю двух разноименно заряженных нитей, проходящих через точки с координатами х = l, у = z = 0 (первая нить) и х =- l, у - z = 0 (вторая нить) параллельно оси Z. Погонные заряды первой и второй нитей обозначим через τ° и -τ° соответственно. Отметим, что по сравнению с формулами 3.6.3 здесь изменены обозначения (и0, V0 и τ° вместо и, V и τ т). Величины h,l и асвязаны соотношением (3.56), аV°и τ°-формулой (3.57), в которой нужно только заменить Vна V ° и τ°на τ°. В соответствии с формулой (3.49) имеем
Подчеркнем, что формулы (10.63) и (10.64) являются строгими и справедливы при любом расстоянии d между проводами. На рис.10.35 показана построенная на основе формул (10.63) и (10.64) структура поля двухтактной ТЕМ-волны в поперечном сечении симметричной двухпроводной линии. Зная напряженность магнитного поля, нетрудно найти плотность токов, текущих по проводам. Рассмотрим, например, первый провод. Введем систему цилиндрических координат
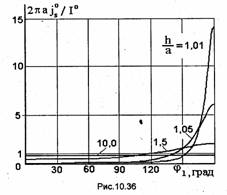
Из полученной формулы видно, что ток в общем случае распределен по периметру провода неравномерно, величина │ j Sm │возрастает при φ1→π. При h>>а эта неравномерность проявляется
слабо, и можно считать, что распределение тока в каждом проводе осесимметрично. При сближении проводов неравномерность распределения тока возрастает. Это приводит к увеличению потерь в линии. Указанное явление называют эффектом близости. На рис. 10.36 показана зависимость функции js° от угла ф, для нескольких значений отношения Л/а, указанных на соответствующих кривых. Коэффициенты ослабления (а) и фазы (Р) двухтактной волны в симметричной двухпроводной линии могут быть вычислены по приближенной формуле, полученной Зоммерфельдом [13]:
электрическая проницаемость и удельная проводимость среды, окружающей линию, а μ r2 и σ2 - относительная магнитная проницаемость и удельная проводимость проводов линии. При выводе формулы (10.67) предполагалось, что имеет место сильно выраженный поверхностный эффект (т.е. выполняется неравен-
При анализе волн в многопроводных линиях обычно используют методы, не учитывающие эффект близости. При близком расположении проводов эти методы могут привести к заметным погрешностям. Представление о влиянии эффекта близости на затухание волн в двухпроводной линии дает рис. 10.37, на котором показана зависимость отношения истинных значений коэффициента ослабления αм к его значениям αм °, вычисленным в предположении осесимметричного распределения тока в каждом проводе, т.е. без учета эффекта близости. Приведенный график рассчитан для случая двухтактной волны в симметричной двухпроводной линии с алюминиевыми проводами при а =.3 мм и f=1 МГц. Как видно, при близком расположении проводов неучет эффекта близости приводит к существенной погрешности. Волновое сопротивление идеальной двухпроводной линии вычисляется по формуле ZB= 2 V°//°. Для двухтактной волны
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.192.174 (0.007 с.) |


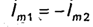


 связанных с координатами х, у, z соотношениями
связанных с координатами х, у, z соотношениями