
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальний закон розподілу випадкової похибки. Середньо-квадратичне значення та дисперсія випадкової похибки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Випадкова похибка — складова загальної похибки вимірювання, яка змінюється випадковим чином (як за знаком, так і за величиною) під час повторних вимірювань однієї і тієї ж величини. Нормальний розподіл (розподіл Ґауса) — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності
де μ — математичне сподівання, σ2 — дисперсія випадкової величини. Нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Наприклад, відстань від влучення снаряду гармати до цілі при великій кількості пострілів характеризується саме нормальним розподілом. Диспе́рсія є мірою відхилення значень випадкової величини від центру розподілу. Більші значення дисперсії свідчать про більші відхилення значень випадкової величини від центру розподілу. Якщо дисперсія дорівнює 0, то всі реалізації випадкової величини знаходяться в одній точці. Нехай випадкова змінна X може набувати значення Дисперсією випадкової величини X називається математичне сподівання квадрату відхилення цієї величини від її математичного сподівання (середнього значення). Дисперсія є центральним моментом другого порядку. Дисперсія дискретної випадкової величини X має такий вигляд:
де Дисперсія абсолютно неперервної випадкової величини
де Математичне сподівання, середнє значення є однією з основних числових характеристик кожної числової змінної. Воно є узагальненим поняттям середнього значення сукупності чисел на той випадок, коли елементи множини значень цієї сукупності мають різну "вагу", ціну, важливість, пріоритет, що є характерним для значень випадкової змінної. Нехай дискретна випадкова змінна X може набувати значення Математичним сподіванням будь-якої дискретної величини називається сума всіх можливих для неї значень, помножених на ймовірності їх (визначення П.Л. Чебишева):
де № 83 Електронні осцилографи, призначення та узагальнена структурна схема. Фунціональні можливості осцилографа при дослідженні електричних сигналів. Електронний осцилограф — це вимірювальний прилад з електронно-променевою трубкою, призначений для дослідження та реєстрації швидкоплинних процесів у електричних колах. У більшості випадків електронні осцилографи використовують для досліджень періодично змінюваних процесів. Але при використанні електронно-променевих трубок з післясвіченням осцилографами можна користуватись і для досліджень неперіодичних, одноразових процесів. Цими приладами можна вимірювати величини напруги, струму, частоти, зсуву фаз, досліджувати форму кривої змінної напруги, визначати характеристики магнітних матеріалів та нелінійних опорів. Їх можна використовувати як нуль-індикатори у схемах порівняння напруг змінного струму. Структурно-функціональну схему електронно-променевого осцилографа показано на рис. Досліджуваний електричний сигнал подають на гнізда, позначені як Y. Подільником напруги ПНУ величина напруги досліджуваного сигналу знижується до рівня, придатного для підсилення на попередньому підсилювачі ПГПҐ (а це десяті — соті частки вольта) і підсилюється ним, а потім і підсилювачем вертикального відхилення ПВВ, вихідні затискачі якого з'єднано з пластинами вертикального відхилення електронного променя електронно-променевої трубки ЕПТ. Разом з тим попередньо підсилений досліджуваний сигнал через правий (на схемі) контакт перемикача сигналів синхронізації Псинх проходить на вхід пристрою синхронізації ПС, а через нього — на генератор розгортки ГР, який генерує напругу пилкоподібної форми, такої, як показано на рисунку. Після підсилення цієї напруги підсилювачем ПГВ, напруга створює між вертикально розташованими пластинами горизонтальної розгортки електричне поле, яке з часом рівномірно збільшуючись, відхиляє електронний промінь. Якщо напруги на гніздах Y немає, то цей промінь креслить на екрані осцилографа горизонтальну пряму лінію.
Структурно-функціональна схема електронно-променевого осцилографа Якщо ж напруга на гніздах Y є, то на електронний промінь одразу діятимуть дві взаємно перпендикулярні сили, завдяки чому цей промінь креслитиме залежність напруги, прикладеної до гнізд Y, від часу, наприклад синусоїду напруги мережі, якщо гнізда Y з нею десь з'єднані, тощо. Важливе значення у роботі осцилографа має пристрій синхронізації ПС, який дає змогу за допомогою попередньо підсиленої напруги UY керувати роботою генератора розгортки, а точніше — примушувати його починати роботу, тобто пересувати електронний промінь упоперек екрана у певний час, наприклад у момент початку збільшення напруги Uy від нуля у позитивний бік. Це сприятиме тому, що за періодично горизонтальної розгортки всі наступні зображення періодично-змінної напруги точно накладатимуться одне на одне і зображення на екрані буде стійким, як нерухомий рисунок. При бажанні керувати розгорткою за допомогою зовнішнього сигналу, перемикач синхронізації (Псинх) переводять у положення "З" (зовнішня). В цьому разі внутрішній зв'язок між напругою UY, що спостерігається, і розгорткою розривається. У більшості осцилографів (окрім показаних на схемі перемикачів) є ще перемикач виду розгортки: "періодична — чекаюча". Періодична — це та, що працює весь час роботи осцилографа й синхронізується періодичною досліджуваною напругою Uy або зовнішніми сигналами. Чекаюча розгортка — це така, що зовсім не працює за відсутності напруги UY. В цьому разі на екрані є лише світна крапка (звичайно з лівого боку), а розгортка починає діяти лише з моменту появи напруги UY. Такою розгорткою доцільно користуватись при дослідженні випадкових чи імпульсних процесів. Якщо ці процеси не повторюються, то доцільно користуватись осцилографом, у якому електронно-променева трубка має значне післясвічення, бо в разі його відсутності спостерігач не встигає розгледіти подробиці процесу. Іноді необхідно розглядати водночас дві напруги у взаємодії. У таких випадках перемикач Проз, який переводять у нижнє положення, зовсім вимикає розгортку, а на пластини X, що керують променем, подають поділену ПНХ і підсилену підсилювачами ППХ і ПГВ напругу, що надходить із гнізд X. У цьому разі на екрані електронно-променевої трубки будуть викреслюватись так звані фігури Ліссажа, за якими можна визначити величину кута зсуву фаз між напругами Ux і Uy, досить точно виміряти величину частоти невідомого джерела змінного струму тощо.
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

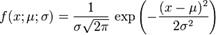
 відповідно з ймовірностями
відповідно з ймовірностями 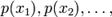 причому
причому 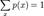 .
.
 і називається стандартним відхиленням величини X від її середнього значення; D — це оператор дисперсії випадкової величини;
і називається стандартним відхиленням величини X від її середнього значення; D — це оператор дисперсії випадкової величини; виглядає так:
виглядає так: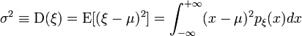
 , тобто це середнє значення величини
, тобто це середнє значення величини  ;
;  — функція густини імовірності.
— функція густини імовірності.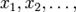 відповідно з ймовірностями
відповідно з ймовірностями  причому
причому 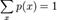 .
.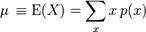
 — це середнє значення випадкової величини X, областю можливих значень якої є множина
— це середнє значення випадкової величини X, областю можливих значень якої є множина  ; E — оператор математичного сподівання; E (X) — математичне сподівання величини X.
; E — оператор математичного сподівання; E (X) — математичне сподівання величини X.



