
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення поля розсіювання розмірів під час механічної обробкиСодержание книги
Поиск на нашем сайте
Розглянемо спочатку визначення сумарної похибки обробки великої партії заготовок на попередньо налагоджувальному верстаті методом автоматичного отримання розміру. При цьому врахуємо, що установка заготовок проводиться у пристрої, обробка їх виконується за велику кількість настроювань. Сумарну похибку або поле розсіювання потрібного розміру можна подати у вигляді наступної функціональної залежності:
де
Завдання визначення сумарної похибки механічної обробки можна порівняти із завданням визначення допуску на замикаючій ланці розмірного ланцюга. При вирішенні цього завдання по максимуму та мінімуму складові виразу (1.29) алгебраїчно сумують:
Сумарну похибку діаметральних розмірів, а також розміру, що сполучає два протилежних елементи, які підлягають одночасній обробці цільним або набірним інструментом, слід визначати без урахування складової Розглянемо другий закон підсумування первинних похибок. Застосовуючи метод неповної взаємозамінюваності, сумування перших п’яти членів виразу (1.29) можна проводити відповідно до
де t - коефіцієнт, що характеризує процент ризику отримання браку в процесі обробки, і дорівнює t=1 при проценті ризику 32%, t=2-4,5% та t=3-0,27%;
Приймаючи t=3,
а з урахуванням похибок форми сумарна похибка потрібного розміру складе
При визначенні сумарної похибки діаметральних розмірів складова Слід відзначити, що у разі наявності невеликої партії деталей їх обробку можна здійснити без зміни інструменту, складовою ΔН у наведених виразах можна знехтувати і та сумарна похибка, як різниця граничних розмірів оброблених деталей, зменшиться. Але в результаті поле величини Δ зміститься в той чи інший бік, величина зміщення не має впливу на поле розсіювання розмірів деталей даної партії. Метод автоматичного отримання розмірів у певних випадках доцільно застосовувати при дуже малих партіях деталей, що дозволить знизити фактичну сумарну похибку у порівнянні з розрахунковою за наведеними формулами. Це обумовлено тим, що дійсний розмірний знос у даних конкретних умовах буде менше відносно регламентованої величини. Крім того, при малих партіях різниця граничних значень припусків і твердості заготівок, по яких визначається ∆n, теж зменшується. Тепер розглянемо сумарну похибку індивідуально оброблюваної заготовки методом пробних проходів:
де
У даному разі сумування первинних похибок виконуємо алгебраїчно з урахуванням можливості їх часткового або повного перекриття та взаємної компенсації. При обробці циліндричної поверхні жорсткої заготовки сумарна похибка діаметрального розміру буде
Величина
Причинний зв’язок між випадковими похибками та викликаючими їх факторами іноді буває відомий (явний), а іноді не зовсім з’ясований. Наприклад, для певного випадку обробки може бути виявлена залежність пружних відтиснень технологічної системи від припуску. В той же час фактори, що викликають розкид діаметрів отворів, які оброблені однією розгорткою, є ще нез’ясованими. Незважаючи на те, що визначення випадкової похибки для кожної деталі в партії практично нездійсненне, можна встановити межі її зміни. При явно виявленому зв’язку між випадковою похибкою та викликаючому її факторами межі зміни можуть бути визначені аналітичними розрахунками. Наприклад, різницю граничних відстаней від вибраної вимірювальної бази до оброблюваної поверхні, що являє собою похибки базування, можна розрахувати по допусках на розміри заготовки. У свою чергу, при неявному зв’язку межі зміни випадкової величини можуть бути встановлені на базі експериментальних досліджень. У цілому, практично не одна з розглянутих похибок не виявляється у чистому вигляді, і тому розподіл простіших закономірно-змінних похибок описується складними математичними рівняннями. Очікувана точність обробки різанням може бути встановлена статистичним або розрахунково-аналітичним методами. Статистичний метод базується на теорії імовірностей і математичної статистики. Він застосовується при визначенні похибок обробки заготовок великого числа (не менше 50) способом автоматичного отримання розмірів. Цей метод широко застосовується в машинобудуванні. Розрахунково-аналітичний метод заснований на виявленні причин виникнення похибок у процесі обробки та встановленні закономірності зменшення цих похибок при наступній обробці. Статистичний метод дослідження. Цей метод не дозволяє безпосередньо виявити вплив усієї сукупності факторів на точність обробки, а отже встановити причини виникнення похибок і шляхи підвищення точності. Іншими словами, даний метод оцінює одночасно вплив усіх факторів і за результатами вимірювання розмірів робляться висновки про точність обробки. До переваг цього методу слід також віднести можливість визначення точності обробки у виробничих умовах без проведення спеціальних досліджень, але регламентувати умови обробки. Статистичний метод оцінки точності обробки використовують в умовах виготовлення великої кількості деталей. Закон нормального розподілу (крива Гаусса). Уявлення про похибки обробки дає крива нормального розподілу дійсних розмірів (індекс “д”) (рис.1.15).
Рис. 1.15 – Крива нормального розподілу дійсних розмірів
Побудова кривої здійснюється на підставі даних вимірювань певного перерізу деталей партії за заданим розміром. Спочатку отримані дані заносять в таблицю східним рядом чисел, установлюють інтервали розмірів (не менше шести), які повинні бути в 2 рази більше ціни поділки шкали вимірювального інструменту. При цьому по осі абсцис відкладають розміри деталей, а ординат – абсолютну або відносну частоту. Абсолютна частота „і” визначається числом m деталей, розмір яких знаходиться в даному інтервалі. Відносна частота (частість) являє собою відношення m деталей у даному інтервалі до загального числа n деталей у досліджуваній партії. Побудова та вивчення кривих розподілу похибок дозволяє відокремити вплив сталих систематичних похибок від випадкових, а також прогнозувати їх значення на підставі обстеження раніше оброблених партій деталей. Це передбачення базується на законі великих чисел, відповідно до якого при зростанні числа спостережень над однорідними явищами частота появи якої-небудь події в минулому наближається до імовірності її появлення в майбутньому. Крива розподілу дійсних розмірів характеризується такими параметрами: 1. полем розсіювання 2. середнім арифметичним значенням дійсних розмірів
для симетричних кривих (при збіганні центру групування з серединою поля допуску)
3. зміщенням центру групування від середини поля допуску
4. середнім квадратичним відхиленням
При великих значеннях Систематична стала похибка не впливає на форму кривої розподілу дійсних розмірів, але зміщує по її осі абсцис. Наприклад, якщо обробляти партію заготовок при одному встановленні різального інструменту на розмір, а потім аналогічну партію при іншому налагодженні інструменту на розмір, то криві розподілу розмірів двох партій будуть зміщені одна відносно другої на величину ∆н цієї похибки. У свою чергу, систематична закономірно-змінна похибка в партії впливає на форму кривої нормально розподілу і збільшує поле розсіювання розмірів. Так, якщо обробити велику партію заготовок і побудувати криву
Рис. 1.16 – Теоретична крива нормального розподілу
Рис. 1.17 – Оцінка точності обробки кривих
Крива Гаусса описується рівнянням
де ℓ - основа натурального логарифма; a - значення абсциси, при якій ордината кривої досягає максимуму. Величина а є центром розподілу (групування) аргумента і в той же час його середньою арифметичною. При абсцисі х=а=
Дана крива асимптотично наближається до осі абсцис. Вона має дві точки перегину А і В на відстані
а ординати їх будуть
При вказаному законі розподілу 25% усіх деталей партії знаходиться в інтервалі Слід відзначити, що прийнята величина поля розсіювання є умовною. При Розрахувавши для оброблених деталей величину До суттєвих недоліків даного методу відноситься те, що за допомогою цього не розкривається сутність фізичних явищ і факторів, що впливають на точність обробки, а також не виявляються конкретні можливості підвищення точності. Метод фіксує результати закінченого етапу. Практика показує, що при недосить вірогідному вимірюванні значення величини можуть коливатися в широких межах (на кілька десятків відсотків в обидва боки від дійсної величини). Це створює деяку невпевненість в оцінці неточності досліджуваного методу. Отримані раніше значення не можуть бути використані, якщо в умовах виконання даної операції відбулися зміни (режим різання, спосіб установлення заготовки). У цьому разі треба виявити нове значення величини з урахуванням конкретних умов обробки. Закон розподілу суттєво додатних величин. Додатною величиною у машинобудуванні називають параметри якості виробу, що характеризуються додатними числами і передвизначають форму виробу. До них відносять ексцентриситет, паралельність, биття, перпендикулярність. Розподіл суттєво додатних величин не підкоряється закону нормального розподілу через те, що технологічний процес повинен забезпечувати номінальні розміри, які відповідають нульовим значенням додатніх величин. Для цих кривих характерна правостороння асиметрія кривих розподілу, параметрами яких є розсіювання та частість. У результаті побудови теоретичної та дійсної кривих можна визначити точність досліджуваного процесу, а також величину імовірного та фактичного браку в %.
Метод точкових діаграм. Незважаючи на відзначені вище переваги статистичного методу відносно оцінки в цілому точності застосовуваних процесів, він не дає змоги розглянути зміну розмірів деталей залежно від часу. Тому систематичні змінні похибності не можуть бути відділені від випадкових. З цих позицій особливе значення отримав метод точкових діаграм, сутність якого полягає в наступному. Результати обробки усієї партії заготовок наведені графічно у вигляді точкових діаграм (рис. 1.18).
Рис. 1.18 – Точкова діаграма
По осі абсцис відкладають час
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.140.197 (0.01 с.) |

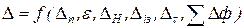 , (1.29)
, (1.29) - похибка (поле розсіювання) розміру в даному перерізі, що виникає в результаті пружних відтиснень технологічної системи під впливом нестабільності сил різання, і дорівнює різниці граничних значень пружніх відтиснень;
- похибка (поле розсіювання) розміру в даному перерізі, що виникає в результаті пружних відтиснень технологічної системи під впливом нестабільності сил різання, і дорівнює різниці граничних значень пружніх відтиснень; - похибка установки, що являє собою суму похибок базування заготовки
- похибка установки, що являє собою суму похибок базування заготовки  , закріплення
, закріплення 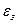 і пристрою
і пристрою  ;
;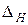 - похибка настроювання верстата і дорівнює різниці між граничними положеннями різального інструменту під час настроювання на потрібний розмір;
- похибка настроювання верстата і дорівнює різниці між граничними положеннями різального інструменту під час настроювання на потрібний розмір;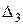 - похибка, пов’язана з розмірним зносом інструменту;
- похибка, пов’язана з розмірним зносом інструменту; - похибка, викликана температурними деформаціями верстата;
- похибка, викликана температурними деформаціями верстата; - cума похибок форми даного елемента, викликана геометричними неточностями верстата, деформаціями заготовки під дією сил закріплення та нерівномірним по різних перерізах заготовки пружним відтисненням технологічної системи від сил різання.
- cума похибок форми даного елемента, викликана геометричними неточностями верстата, деформаціями заготовки під дією сил закріплення та нерівномірним по різних перерізах заготовки пружним відтисненням технологічної системи від сил різання. . (1.30)
. (1.30) . У цілому розрахунок сумарної похибки обробки за формулою (1.30) простий, проте значення
. У цілому розрахунок сумарної похибки обробки за формулою (1.30) простий, проте значення  виходить завищеним і граничні розміри, що відповідають даній величині, навіть при великій партії заготівок будуть зустрічатися рідко. У свою чергу, прийняття технологічного допуску за величиною
виходить завищеним і граничні розміри, що відповідають даній величині, навіть при великій партії заготівок будуть зустрічатися рідко. У свою чергу, прийняття технологічного допуску за величиною  , (1.31)
, (1.31) - коефіцієнти, що залежать від форми кривих розподілу відповідних первинних похибок. Для кривої розподілу, близької до нормального закону -
- коефіцієнти, що залежать від форми кривих розподілу відповідних первинних похибок. Для кривої розподілу, близької до нормального закону -  =1/9, рівній іімовірності та коли про форму кривої розподілу нічого невідомо
=1/9, рівній іімовірності та коли про форму кривої розподілу нічого невідомо  =1/9;
=1/9;  =1/3, вираз (1.31) можна записати у наступному вигляді:
=1/3, вираз (1.31) можна записати у наступному вигляді: , (1.32)
, (1.32) . (1.33)
. (1.33)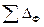 переходить у випадкову і при визначенні ∆ її квадрат вводиться додатком під знак радикалу.
переходить у випадкову і при визначенні ∆ її квадрат вводиться додатком під знак радикалу. , (1.34)
, (1.34) - похибка форми обробленої поверхні, що отримана в результаті копіювання первинних похибок заготовки в умовах пружної технологічної системи при різній жорсткості її в окремих перерізах;
- похибка форми обробленої поверхні, що отримана в результаті копіювання первинних похибок заготовки в умовах пружної технологічної системи при різній жорсткості її в окремих перерізах; - похибка перевірки залежить від кваліфікації робітника, а також виду вимірювального інструменту, що застосовується;
- похибка перевірки залежить від кваліфікації робітника, а також виду вимірювального інструменту, що застосовується; - похибка форми поверхні в результаті розмірного зносу різального інструменту;
- похибка форми поверхні в результаті розмірного зносу різального інструменту; - похибка форми, викликана температурними деформаціями технологічної системи у процесі обробки деталі;
- похибка форми, викликана температурними деформаціями технологічної системи у процесі обробки деталі; - похибка форми оброблюваної поверхні, що виникає через геометричні неточності верстату.
- похибка форми оброблюваної поверхні, що виникає через геометричні неточності верстату.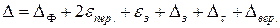 . (1.35)
. (1.35)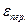 подвоюється, тому що ми її відносимо до діаметрального розміру.
подвоюється, тому що ми її відносимо до діаметрального розміру.
 ;
;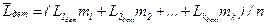 ; (1.36)
; (1.36)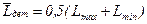 ; (1.37)
; (1.37) ; (1.38)
; (1.38) дійсних розмірів, що характеризує, наскільки точно згруповані можливі значення від центру групування. Воно є єдиним параметром, що визначає форму кривої закону нормального розподілу (рис.1.16), до якої близька крива розподілу дійсних розмірів:
дійсних розмірів, що характеризує, наскільки точно згруповані можливі значення від центру групування. Воно є єдиним параметром, що визначає форму кривої закону нормального розподілу (рис.1.16), до якої близька крива розподілу дійсних розмірів: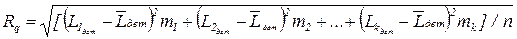 . (1.39)
. (1.39) крива виходить дуже пологою і поле розсіювання росте, а при малих – сильно витягнутою вгору з малим полем розсіювання.
крива виходить дуже пологою і поле розсіювання росте, а при малих – сильно витягнутою вгору з малим полем розсіювання. розподілу для однієї частини заготовок при малому зносі інструменту, а іншу криву
розподілу для однієї частини заготовок при малому зносі інструменту, а іншу криву  для усієї партії, то форми кривої будуть різними (рис.1.17). Це пояснюється збільшенням поля допуску розмірів через підвищений знос різального інструменту.
для усієї партії, то форми кривої будуть різними (рис.1.17). Це пояснюється збільшенням поля допуску розмірів через підвищений знос різального інструменту.

 , (1.40)
, (1.40) крива в центрі групування має максимальне значення ординати
крива в центрі групування має максимальне значення ординати . (1.41)
. (1.41) і
і 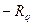 в центрі групування (рис.1.16). Абсциси в точках А і В відповідно дорівнюють
в центрі групування (рис.1.16). Абсциси в точках А і В відповідно дорівнюють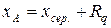 і
і  , (1.42)
, (1.42) . (1.43)
. (1.43)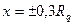 ,
,  ,
, 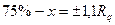 . Коли прийняти інтервал
. Коли прийняти інтервал  , то 99,73% деталей партії будуть знаходитися в полі розсіювання
, то 99,73% деталей партії будуть знаходитися в полі розсіювання 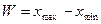 , при цьому похибка складе всього 0,27%. Таким чином, приймаємо
, при цьому похибка складе всього 0,27%. Таким чином, приймаємо  .
. імовірнісна кількість браку знижується мало, а при
імовірнісна кількість браку знижується мало, а при  - зростає. Правило “шести середньоквадратичного відхилення” є досить простим і зручним для практичного користування при об’єктивній оцінці точності процесу обробки, виконуваного в певних умовах. Умовність цього правила не виключає в окремих випадках застосування іншого коефіцієнта замість шести.
- зростає. Правило “шести середньоквадратичного відхилення” є досить простим і зручним для практичного користування при об’єктивній оцінці точності процесу обробки, виконуваного в певних умовах. Умовність цього правила не виключає в окремих випадках застосування іншого коефіцієнта замість шести. , можна знайти поле розсіювання
, можна знайти поле розсіювання 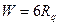 , стає можливим вибрати відповідний метод обробки, що забезпечує задану точність. Таким способом можна виконати вирішення й інших технологічних задач, що стосуються обробки різанням. Крім того, дослідження точності обробки за допомогою кривих розподілу дозволяє скласти таблиці точності різних способів обробки. Особливе значення набувають таблиці у випадках, коли точність обробки залежить від виробничих похибок, які врахувати аналітичним шляхом неможливо.
, стає можливим вибрати відповідний метод обробки, що забезпечує задану точність. Таким способом можна виконати вирішення й інших технологічних задач, що стосуються обробки різанням. Крім того, дослідження точності обробки за допомогою кривих розподілу дозволяє скласти таблиці точності різних способів обробки. Особливе значення набувають таблиці у випадках, коли точність обробки залежить від виробничих похибок, які врахувати аналітичним шляхом неможливо.
 роботи або номери послідовно оброблюваних заготовок (груп заготовок), а по осі ординат – для наочності характеру зміни групові середні
роботи або номери послідовно оброблюваних заготовок (груп заготовок), а по осі ординат – для наочності характеру зміни групові середні  розміри. Розкид точок характеризує розсіювання розмірів по вертикалі та зміну їх, що пов’язані з підналагодженням верстата. Перевага даного методу полягає в можливості контролю процесу та своєчасного усунення помічених відхилень від правильного виконання операції. На рис. 1.18 нанесені дві прямі, що відповідають максимальному і мінімальному розмірам по кресленню, а також дві контрольні прямі АА та ВВ. При наближенні відповідних точок вимірювання до контрольної прямої (при зовнішній обробці – до верхньої, а при внутрішній – до нижньої) необхідно здійснювати підналагодження верстата.
розміри. Розкид точок характеризує розсіювання розмірів по вертикалі та зміну їх, що пов’язані з підналагодженням верстата. Перевага даного методу полягає в можливості контролю процесу та своєчасного усунення помічених відхилень від правильного виконання операції. На рис. 1.18 нанесені дві прямі, що відповідають максимальному і мінімальному розмірам по кресленню, а також дві контрольні прямі АА та ВВ. При наближенні відповідних точок вимірювання до контрольної прямої (при зовнішній обробці – до верхньої, а при внутрішній – до нижньої) необхідно здійснювати підналагодження верстата.


