
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Випадковий процес. Основні моментні функції.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Випадковим процесом називається функція Реалізацією випадкового процесу
Однак зовсім необов'язково, щоб випадкові процеси були складними, з нерегулярною за часом поведінкою, функціями. Часто доводиться мати справу з випадковими процесами, утвореними гармонічними сигналами Моментні функції випадкових процесів Менш докладні, але цілком задовільні у практичному плані характеристики випадкових процесів можна отримати, обчислюючи моменти тих випадкових величин, які знаходяться в перетинах цих процесів. У загальному випадку ці моменти залежать від часових аргументів, тому отримали назву моментних функцій. Найбільше значення у статистичній радіотехніці мають три моментних функції: математичне сподівання, дисперсія та функція кореляції. Математичне сподівання. Одновимірну моментну функцію першого порядку
називають математичним сподіванням випадкового процесу. В загальному випадку математичне сподівання випадкового процесу різне для різних моментів часу, тому воно є функцією параметра
Дисперсія Центральну моментну функцію другого порядку називають дисперсією випадкового процесу:
Дисперсія визначає ступень розкиду миттєвих значень окремих реалізацій у фіксованому перетині відносно середнього значення.
Кореляційна функція Кореляційна функція – це функція, що характеризує ступінь залежності між перетинами випадкового процесу, взятими в різні моменти часу. Функція кореляції випадкового процесу є двомірною центральною моментною функцією другого порядку
де
Спектральний метод аналізу проходження випадкових сигналів через лінійні електричні кола. На вході лінійного стаціонарного кола розглянемо випадковий стаціонарниі процес
залежить лише від величини Середнє значення вихідного сигналу Виразимо реалізацію х(ї) вхідного сигналу Х(і) за допомогою інтеграла Фур'є
Вихідний сигнал можна знайти, якщо відомим буде коефіцієнт передачі
Переходячи від окремої реалізації до ансамблю вхідних сигналів, слід врахувати, що, як відомо, у випадку стаціонарного процесу середнє значення спектральної густини дорівнює нулеві Тому, виконуючи усереднення в обох частинах рівності (8.2), матимемо:
Кореляційна функція та спектральна густина потужності випадкового сигналу на виході системи Функцію кореляції вихідного сигналу будемо шукати за формулою
Тут реалізація
Формула (8.5) не зміниться, якщо в її правої частини перейти до комплексно-спряжених величин:
Тоді
Врахуємо, що вхідний сигнал стаціонарний, тому, як відомо, випадкові спектральні густини його окремих реалізацій дельтакорельовані, тобто
де
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 , кожне миттєве значення якої (при
, кожне миттєве значення якої (при  ) є випадковою величиною
) є випадковою величиною  . Випадкове значення
. Випадкове значення  .
. , на яку перетворюється випадковий процес
, на яку перетворюється випадковий процес  знаходять певну реалізацію
знаходять певну реалізацію  – номер досліду) дає кілька різних реалізацій випадкового процесу:
– номер досліду) дає кілька різних реалізацій випадкового процесу:  , або статистичний ансамбль (сім’ю) реалізацій, наприклад, набір сигналів (рис. 7.5), які можна спостерігати на виходах
, або статистичний ансамбль (сім’ю) реалізацій, наприклад, набір сигналів (рис. 7.5), які можна спостерігати на виходах  однакових генераторів шумової напруги.
однакових генераторів шумової напруги. , у яких один з трьох параметрів
, у яких один з трьох параметрів  - випадкова величина. При скінченній кількості параметрів випадковий процес прийнято називати квазідетермінованим випадковим процесом.
- випадкова величина. При скінченній кількості параметрів випадковий процес прийнято називати квазідетермінованим випадковим процесом. (7.51)
(7.51) . (7.52)
. (7.52)
 (7.53)
(7.53) – ймовірність того, що в момент часу
– ймовірність того, що в момент часу  функція
функція  до
до  , а в момент
, а в момент  – в інтервалі від
– в інтервалі від  до
до 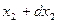 .
. , у якого, як відомо, математичне сподівання стале у часі і для простоті дорівнює:
, у якого, як відомо, математичне сподівання стале у часі і для простоті дорівнює:  . Функція кореляції
. Функція кореляції
 . Визначимо статистичні характеристики вихідного сигналу.
. Визначимо статистичні характеристики вихідного сигналу. . (1)
. (1) :
: . (2)
. (2) .
. . (3)
. (3) . (4)
. (4)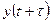 визначається аналогічно реалізації
визначається аналогічно реалізації  :
: . (5)
. (5)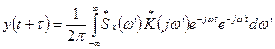 . (6)
. (6)
 . (7)
. (7) , (8)
, (8) - спектр потужності стаціонарного випадкового процесу
- спектр потужності стаціонарного випадкового процесу 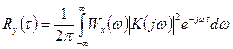 . (9)
. (9)


