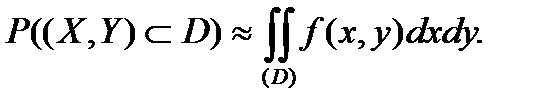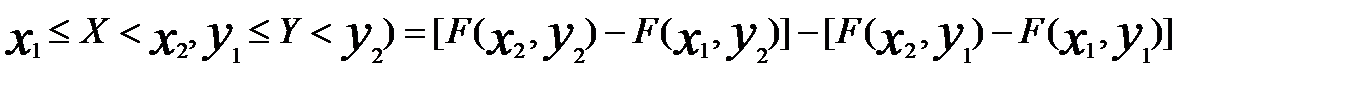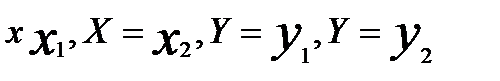Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дати означення системи випадкових величин.Содержание книги
Поиск на нашем сайте Системою випадкових величин Х1, Х2,...,Хn називають сукупність цих ВВ, які вивчаються або розглядаються одночасно(СВВ).(Х;У), (Х;У;Z)... Систему n ВВ (Х1, Х2,...,Хn) можна розглядати як випадкову точку в n-вимірному просторі з координатами (Х1, Х2,...,Хn) або як випадковий вектор, напрямлений з початку координат у точку М (Х1,Х2,...,Хn) Законом розподілу ДВВ називається перелік можливих значень цієї величини (хі, уk) та їх імовірностей р(хі, уk), і=1,2,..., n; k=1,2,...,m Найбільш часто закон розподілу двв задають у вигляді таблиці з двома входами. Закон розподілу двв дозволяє отримати закони розподілу кожної компоненти. 3.коефіцієнт кореляції –це кількісна характеристика залежності випадкових величин X та Y і часто використовується в статистиці r XY= Випадкові величини та звуть некорельованими якщо їх кореляційний момент або коефіцієнт кореляції дорівнює нулю. Властивості:1.! rXY!≤1 2.Якщо X та Y незалежні то r XY=0 3.якщо між X та Y є лінійна залежність Y=aX+b де а і b–постійні, то!rXY!=1 Вибірковий коефіцієнт кореляції визначається
4. Для перевірки правильності основної статистичної гіпотези Но необхідно: 1) визначити гіпотезу Н1, альтернативну до гіпотези Но; 2) обрати статистичну характеристику перевірки; 3) визначити допустиму імовірність похибки першого роду, тобто рівень значущості α; 4) знайти за відповідною таблицею критичну область (критичну точку) для обраної статистичної характеристики. До критичної області належать такі значення статистичної характеристики, при яких гіпотеза Но відхиляється на користь альтернативної гіпотези Н1. Якщо гіпотеза Но правильна, то з імовірністю α значення вибіркової функції будуть належати критичній області. Так, при перевірці гіпотези Но про рівність дисперсій двох нормальних сукупностей при альтернативній H1: D(X)>D(Y) Треба знайти спостережене значення критерія Фішера-Снедекора, тобто Fcn=S1*S1/S2*S2, А потім з таблиці критичних точок цього розділу по заданому рівню значущості α та степенях вільності k1=n1-1 та k2=n2-1 знайти Fkp (α; k1; k2). Якщо Fcn<Fkp, то гіпотеза Но приймається. Якщо Fcn>Fkp, то Но відхиляють. 5.Дати означення ф-ціїї розподілу двв. Основні властивості ф-ції розподілу, її геометричний зміст. Ф-цією розпділу двв (Х,У) називають ф-цію 2-х змінних F(х,у), яка визначає для кожної пари чисел (Х,У) імовірність виконання нерівностей X<x; Y<y, тобто F(x,y)=P(X<x; Y<y). Аналогічно визначають ф-цію розподілу n вв: F(х1,х2,…,xn)= P(X<x; Y<y,…, Xn<xn) Властивості: 0≤ F(x,y)≤1; F(х,у)не спаднка ф-ція за кожним аргументом, тобто F(x2,y)≥ F(x1,y), якщо x2> x1; F(x,y2) >F(x,y1), якщо у2> у1; Мають місце граничні співвідношення: F(-∞,y)=0; F(x1,∞-)=0; F(∞,∞)=1; Імовірність влучення випадкової точки до прямокутника { x1 ≤Х ≤х2; у1 ≤У≤ у2}можна знайти за формулою: Р(x1 <Х <х2; у1 <У< у2)= {F(х2,у2)- F(х1,у2)}- {F(х2,у1)- F(х1,у1)} Геометричний зміст ф-ї розподілу F(х,у) – це імовірність того, що випадкова точка М(Х,У), попаде у нескінченний прямокутник з вершиною в т.(Х,У) і розміщений нижче та лівіше цієї вершини М(Х,У) 6.Дати означення щільності розподілу імовірностей двовимірної випадкової величини. Навести її основні властивості та імовірнісний зміст. Записати формули для обчислення імовірності влучення випадкової точки:а) в довільну двовимірну область Д; б) в прямокутник зі сторонами, паралельними осям координат. Пояснити зміст позначень.
Законом розподілу дискретної двохвимірної випадкової величини називають перелік можливих значень цієї величини ( Законом розподілу двохвимірної випадкової величини дозволяє отримати закони розподілу кожної компоненти. Властивість 1: Двовимірна платність імовірності не додатня: f(x,y)≥0 Доведення: Ймовірність попадання випадкової точки в прямокутник зі сторонами ∆х і ∆у є не додатнє число;площа цього трикутника позитивне число. Следоватильно, відносини цих двох чисел, а значить і їх приділ (при ∆х f(x,y)≥0
Властивість 2: Подвійний несобственний інтеграл з безкінечними приділами від двомірної платності =1
Доведення: Безкінечні приділи інтегрірованія вказують що обласю інтегріровання слугує вся плоскість хОу; поскільки подія состоящач в тому що випадкова точка попаде при експерименті на плоскість хОу, дійсно,то ймовірність цієї події =1.
А) Б)P( X= Питання №7
|
||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

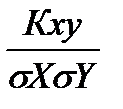
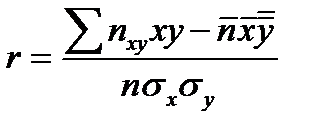 , де x,y –варіанти ознак X та Y, nxy – частота пари варіант, n –обєм вибірки, σx,σy –вибіркові середні квадратичні відхилення,
, де x,y –варіанти ознак X та Y, nxy – частота пари варіант, n –обєм вибірки, σx,σy –вибіркові середні квадратичні відхилення, 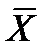 ,
, 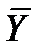 - вибіркові середні. Відомо, що якщо величини Y та X не залежать, то коефіцієнт кореляції r=0, якщо r= -1, то Y та Х зв´язані лінійною функцією начальною залежністю, звідси слідує, що коефіцієнт кореляції вимірює силу лінійного зв´язку між Y та Х. Вибірковий коефіцієнт кореляції r – являється оцінкою коефіцієнта кореляції r генеральної сукупності і тому слугує для виміру лінійного зв´язку між величинами кількісними ознаками Х та Y. Якщо вибірка має достатньо великий об´єм та добре представляє генеральну сукупність, то заключення про щільність лінійної залежності між ознаками, яке отримано за даними вибірки, в відомій степені може бути розповсюджено і на генеральну сукупність. Приклад – для оцінки коефіцієнта кореляції ry нормально розподіленої генеральної сукупності (при np=50) можна скористатися формулою:
- вибіркові середні. Відомо, що якщо величини Y та X не залежать, то коефіцієнт кореляції r=0, якщо r= -1, то Y та Х зв´язані лінійною функцією начальною залежністю, звідси слідує, що коефіцієнт кореляції вимірює силу лінійного зв´язку між Y та Х. Вибірковий коефіцієнт кореляції r – являється оцінкою коефіцієнта кореляції r генеральної сукупності і тому слугує для виміру лінійного зв´язку між величинами кількісними ознаками Х та Y. Якщо вибірка має достатньо великий об´єм та добре представляє генеральну сукупність, то заключення про щільність лінійної залежності між ознаками, яке отримано за даними вибірки, в відомій степені може бути розповсюджено і на генеральну сукупність. Приклад – для оцінки коефіцієнта кореляції ry нормально розподіленої генеральної сукупності (при np=50) можна скористатися формулою: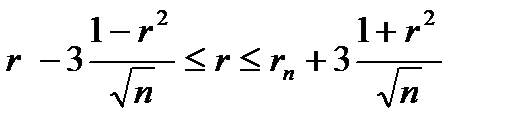
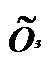 ,
,  ) та їх імовірностей p(
) та їх імовірностей p(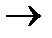 0 і ∆у
0 і ∆у 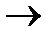 0), які рівні f(x,y) є не додатнє число.
0), які рівні f(x,y) є не додатнє число.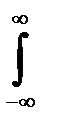
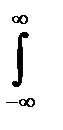 f(x,y)dxdy=1
f(x,y)dxdy=1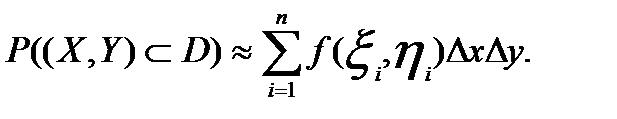 Переходячи до приділу при ∆х
Переходячи до приділу при ∆х