
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивести рівняння лінійної середньоквадратичної регресії y та X (y на X). Пояснити зміст позначень. Дати означення коефіцієнту регресії, залишкової дисперсії та пояснити, що вони характеризують.Содержание книги
Поиск на нашем сайте
Теорема. Лінійна середньоквадратична регресія Y на X має вигляд
Доведення. Розглянемо функцію двох незалежних аргументів
Враховуючи, що М(Х- mx)=М(Y- my)=0, М[(Х- mx)(Y- my)]= Дослідимо функцію
, звідси Отже, лінійна середньоквадратична регресіяY та X має вигляд:
Коефіцієнт
Підставивши знайдені значення 48. Дати означення генеральної та вибіркової середніх. Довести незміщеність вибіркової середньої як оцінки генеральної середньої. Сформулювати властивість стійкості вибіркових середніх. Генеральною середньою Якщо всі значення х1,х2,…,хN ознаки генеральної сукупності об’єму N різні, то
Якщо значення ознаки х1,х2,…,хk N1, N2, …, Nk, причому N1+ N2+ …+ Nk=N, то
Тобто генеральна середня є середня зважена значень ознаки з вагами, що рівні відповідним частотам. Вибірковою середньою Якщо всі значення х1,х2,…,хn ознаки вибіркової сукупності об’єму n різні, то
Якщо значення ознаки х1,х2,…,хk n1, n2, …, nk, причому n1+ n2+ …+ nk=N, то
Тобто вибіркова середня є середня зважена значень ознаки з вагами, що рівні відповідним частотам. Нехай з генеральної сукупності (в результаті незалежних спостережень над кількісною ознакою Х) вилучена повторна вибірка об’єму n зі значеннями ознаки х1,х2,…,хn .Будемо вважати ці значення ознаки різними. Нехай генеральна середня невідома і необхідно оцінити її за даними вибірки. В якості оцінки генеральної середньої приймають вибіркову середню
Впевнимося, що М(Хв)= М[(X1+X2+…+Xn)/n]=a (1) Прийнявши до уваги, що кожна з величин має той же розподіл, що і генеральна сукупність, значить і числові характеристики цих величин і генеральної сукупності однакові. А саме, математичне сподівання а кожної із величин рівне математичному сподіванню ознаки Х генеральної сукупності, тобто М(Х)= Замінивши в формулі (1) математичне сподівання а на М(Хв)= Тим самим доведено, що вибіркова середня є незміщена оцінка генеральної середньої. При збільшенні об’єму вибірки n вибіркова середня прямує по ймовірності до генеральної середньої, а це і значить, що вибіркова середня є состоятельная оцінка генеральної середньої. Якщо по декільком вибіркам достатньо великого об’єму із однієї і тієї ж генеральної сукупності будуть знайдені вибіркові середні, то вони будуть приблизно рівні між собою. В цьому і полягає властивість стійкості вибіркових середніх. 49. Записати випадкові величини, які мають розподіли: а) Пірсона; б)Стьюдента; в)Фішера. Записати функції щільності розподілу ймовірностей для цих розподілів. Пояснити зміст позначень. А) Нехай Хі(і=1, 2,…, n) – нормальні незалежні випадкові величини, причому математичне сподівання кожної із них рівне нулю, а середнє квадратичне відхилення – одиниці. Тоді сума квадратів цих величин
розподілена по закону Щільність цього розподілу
Звідси видно, що цей розподіл визначається одним параметром – числом степенів вільності k. Із збільшенням числа степенів вільності розподіл повільно наближається до нормального. Б) Нехай Z – нормальна випадкова величина, причому М(Z)=0,
Отже, відношення нормованої нормальної величини до квадратного кореня із незалежної випадкової величини, розподіленої по закону Із збільшенням числа степенів вільності розподіл Стьюдента швидко наближається до нормального. В) Якщо U і V – незалежні випадкові величини, розподілені по закону
має розподіл, який називають розподілом F Фішера-Снедекора зі степенями вільності k1 і k2 (інколи його позначають через V Щільність цього розподілу:
Розподіл F визначається двома параметрами – числами степенем вільності. 50. Дати означення функції випадкової величини. Записати формулу для знаходження щільностей імовірностей функції неперервного випадкового аргумента. Навести приклади побудови закону розподілу функції двв та щільності імовірностей функції нвв. Функцією розподілу називають функцію F(x), що определяють ймовірність того, що випадкова величина Х в результаті випробування прийме значення, менше х, тобто F(x)=Р(Х<х). Геометрично це рівність можна истолковать: F(x) це ймовірність того, що випадкова величина прийме значення, яке зображується на числовій осі точкою, що знаходиться лівіше від точки х. Щільність розподілу ймовірностей НВВ Х називають функцію f(x) – першу похідну від функції розподілу F(x)
приклад ДВВ Х задана таблицею розподілу Х 1 4 8\ Р 0,3 0,1 0,6 Знайти функцію розподілу та графік. Розвязок якщо х<=1, то F(x)=0, Якщо 1<х<=4, то F(x)=0,3. Дійсно, х може прийняти значення 1 с ймовірністю 0,3 Якщо 4<х<=8, то F(x)=0,4. Дійсно, якщо х1 удовлєтворяє нерівності 4<х1<=8, то F(x)=ймовірності події Х<x1, яка може бути здійснене, коли Х прийме значення 1, або значення 4. Ці дві події не совмесні, то по теоремі складання імовірність події Х<х1, дорівнює сумі ймовірностей 0,3+0,1=0,4. Якщо більше 8, то F(x)=1. Дійсно, подія х<=8 достовірна, тобто його ймовірність = 1.
Приклад2 Дана функція розподілу неперервної випадкової величини Х. знайти щільність.
Зв'язок: f(x)= 51. Записати формули для обчислення математичного сподівання та дисперсії: а) функції д.в.в.; б) фцнкції н.в.в. Пояснити зміст позначень. Навести приклади. А) Математичним сподіванням д.в.в. суму добутків всіх її можливих значень на їх ймовірності. Нехай випадкова величина Х може приймати тільки значення х1,х2,…,хn, ймовірності яких відповідно рівні р1,р2, …, рn. Тоді математичне сподівання М(Х) випадкової величини Х визначається рівністю: М(Х)=х1р1+х2р2+…+хnpn Якщо д.в.в. Х приймає злічену множину можливих значень, то М(Х)= причому математичне сподівання існує, якщо ряд в правій частині рівності сходиться абсолютно. Приклад 1. Знайти математичне сподівання в.в. Х, знаючи її закон розподілу Х 3 5 2 Р 0.1 0.6 0.3 М(Х)= 3*0.1+5*0.6+2*0.3=3.9 Дисперсією випадкової величини х називається математичне сподівання квадрату відхилення випадкової величини від її математичного сподівання для ДВВ: D(X)=M[X-M(X)] Приклад 2. Знайти дисперсію в.в. Х, яка задана наступним законом розподілу: Х 2 3 5 Р 0.1 0.6 0.3 М(Х D(X)=13,3 – (3,5) Б) Математичним сподіванням н.в.в. Х, можливі значення якої належать відрізку [а, b] називається визначений інтеграл:
Якщо можливі значення належать всій осі,то
Дисперсією н.в.в. називають математичне сподівання квадрату її відхилення. Якщо можливі значення Х належать відрізку [а, b], то
Якщо можливі значення належать всій осі х, то
52. Дати означення емпіричної та теоретичної частот, записати формулу для обчислення теоретичних частот для розподілу Пуассона. Емпіричними частотами називають фактично спостерігаємі частоти ni. Нехай є наміри допустити, що вивчаєма величина Х розподілена по деякому визначеному законом. Щоб перевірити, чи співпадає дане припущення з даними спостереження., вичисляють частоти спостерігаємих значень, тобто знаходять теоретичну частоту ni кожного з спостерігаємих значень в припущення, що величина Х розподілена по припущеному закону. Теоретичні, на відміну від фактичних спостережуваних емпіричних частот називають частоти ni, знайдені теоретично (вичисленням). Теоретичні частоти знаходять за допомогою рівності ni=Рі* n. Для розподілу Пуассона:
У випадку, коли ВВ розподілена нормально, то вирівнюючі частоти можуть бути знайдені за формулою:
Де n- число випробувань (об‘єм вибірки), h-довжина часткового інтервалу, σ-вибіркове середньоквадратичне відхилення, ui=(xi-
Наприклад, для розподілу Пуассона:
Р(0)=0,33469, Р(1)=0,0,251021,….
Хв=34,7. σв=7,38.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.252 (0.011 с.) |

 де mx=M(X), my=M(Y),
де mx=M(X), my=M(Y), 
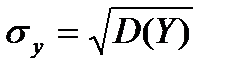 , r =
, r =  - коефіцієнт кореляції величин Y та X.
- коефіцієнт кореляції величин Y та X. і
і  :
: (1)
(1) , і зробивши викладки отримаємо
, і зробивши викладки отримаємо 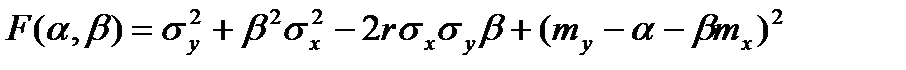
 на екстремум, для чого прирівняємо до нуля частинні похідні:
на екстремум, для чого прирівняємо до нуля частинні похідні:

 і
і  досліджувана функція приймає найменше значення.
досліджувана функція приймає найменше значення. , або
, або 
 називають коефіцієнтом регресії Y на X, а пряму
називають коефіцієнтом регресії Y на X, а пряму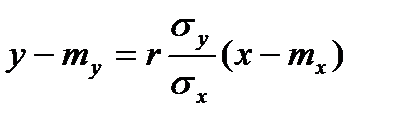 називають прямою середньоквадратичної регресії Y на X.
називають прямою середньоквадратичної регресії Y на X. . Величину
. Величину  називають залишковою дисперсією випадкової величини Y відносно випадкової величини X; вона характеризує величину помилки, яку допускають при заміні Y лінійною функцією
називають залишковою дисперсією випадкової величини Y відносно випадкової величини X; вона характеризує величину помилки, яку допускають при заміні Y лінійною функцією  . При r=
. При r=  1 залишкова дисперсія дорівнює нулю; іншими словами, при цих крайніх значеннях коефіцієнта кореляції не виникає помилки при представленні Y у вигляді лінійної функції від X.
1 залишкова дисперсія дорівнює нулю; іншими словами, при цих крайніх значеннях коефіцієнта кореляції не виникає помилки при представленні Y у вигляді лінійної функції від X. називають середнє арифметичне значень ознаки генеральної сукупності.
називають середнє арифметичне значень ознаки генеральної сукупності. називають середнє арифметичне значення ознаки вибіркової сукупності.
називають середнє арифметичне значення ознаки вибіркової сукупності. =(х1n1+х2n2+…+ хknk)/ n, або
=(х1n1+х2n2+…+ хknk)/ n, або =
=  ,
,
 с k=n степенями вільності; якщо ж ці величини зв’язані одним лінійним співвідношенням, наприклад
с k=n степенями вільності; якщо ж ці величини зв’язані одним лінійним співвідношенням, наприклад  , то число вільності k=n-1.
, то число вільності k=n-1. , де
, де - гамма-функція, а саме Г(n+1)=n!
- гамма-функція, а саме Г(n+1)=n! , а V – незалежна від Z величина, яка розподілена по закону
, а V – незалежна від Z величина, яка розподілена по закону 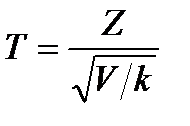 має розподіл, який називають t-розподілом або розподілом Стьюдента з k степенями вільності.
має розподіл, який називають t-розподілом або розподілом Стьюдента з k степенями вільності.
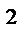 )
)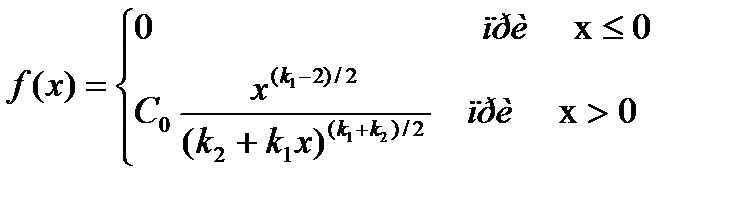 , де
, де
 , з ціого означення випливає, що функція розподілу є першообразною для щільності розподілу
, з ціого означення випливає, що функція розподілу є першообразною для щільності розподілу

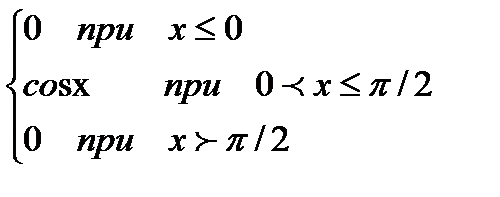


 )=4*0.1+9*0.6+25*0.3=13.3
)=4*0.1+9*0.6+25*0.3=13.3 =1,05
=1,05





 B)/σ.
B)/σ.




