
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Що в теорії ймовірностей розуміють під терміном «закон великих чисел». Записати нерівність А. Чебишова. Пояснити зміст букв.Содержание книги
Поиск на нашем сайте
Що в теорії ймовірностей розуміють під терміном «Закон великих чисел»? Записати нерівність А. Чебишова. Пояснити зміст букв. Граничні теореми теорії ймовірностей встановлюють відповідність між теоретичними та дослідними характеристиками випадкових величин або випадкових подій при великій кількості випробувань. Граничні теореми описують також граничні закони розподілу. Граничні теореми, які встановлюють відповідність між теоретичними та дослідними характеристиками випадкових подій, об’єднують загальною назвою – закона великих чисел. Перша форма нерівності Чебишова. Для довільної випадкової величини Х, яка приймає невід’ємні значення та має скінчене математичне сподівання Р(Х≥1)≤М(Х). Якщо Х – дискретна випадкова величина, то Р(Х≥1) = Якщо Х – неперервна випадкова величина, f(x) – щільність її імовірностей, то
Р(Х≥1) = Друга форма нерівності Чебишова. Якщо випадкова величина Х має скінчені математичне сподівання та дисперсію, то для довільного ε>0 має місце нерівність
Питання №7 СТАТИСТИЧНІ КРИТЕРІЇ ТА ОБЛАСТІ
1. Статистичний критерій – випадкова величина К, розподіл якої (точний або наближений) відомий і яка застосовується для перевірки основних гіпотези Якщо статистична характеристика розподілена: - нормально,то критерій позначають не К, а літерами U або Z - за законом Фішера-Снедекора, то F - за законом Стьюдента, то Т - за законом «Xi-квадрат», то 2. Спостереженим значенням критерію узгодження називають значення відповідного критерію, обчислене за даними вибірки. 3. Критчною областю називають сукупність значень критерію, при яких основа гіпотеза відхиляється. 4. Областю прийняття гіпотези (областю допустимих значень) називають множину значень критерію, при яких гіпотезу приймають. 5. Критичними точками (межами) критерію К називають точки «Ккр», які відокремлюють критичну область від області прийняття гіпотези. 6. Розрізняють однобічну (правобічну та лівобічну) та двобічну критичні області. Правобічною називають критичну область, що визначається нерівністю К>Ккр, де Ккр – додатне число. Лівобічною називають критичну область, що визначається нерівністю К<Ккр, де Ккр – відємне число.
Дати означення умовного закону розподілу складових системи д.в.в. Записати формули для обчислення умовних ймовірностей складових систем д.в.в. Пояснити зміст позначень. Дати означення умовної щільності імовірностей складових системи н.в.в.
Умовним розпреділенням складаючий Х при У=
Умовна щільність
Питання №9 19.
Що є предметом теорії ймовірностей? Дати визначення підмножини, скінченної, нескінченної, зліченої і незліченої множин. Навести приклади. Предметом ТЙ є вивчення ймовірнісних закономірностей масових однорідних випадкових подій. Підмножина – частина множини. Будь – яка множина є підмножиною самої себе. Множина наз. нескінченною (скінченною), якщо вона має нескінченне (скінченне) число елементів. Нескінченна множина наз. зліченою (незліченою), якщо її елементи можна (неможна) пронумерувати. Приклади: 1) якщо Х- множина відмінників групи, то 2) Дати означення випадкового експерименту, випадкової події, неможливої та достовірної подій. Навести приклади. Дати означення елементарного наслідку випадкового експерименту, простору елементарних наслідків. Експеримент (випробування) – реалізація певної сукупності умов, в результаті якої настає певна подія. Експеримент наз. випадковим, якщо в результаті його проведення може настати деяка подія. Випадковою називають таку подію, яка при умовах, що розглядаються,може трапитися, а може й не трапитися. Неможливою називають таку подію, яка при розглянутих умовах не може трапитися. Достовірною називають таку подію, яка при розглянутих умовах обов’язково трапиться. Приклади: Якщо в урні є лише білі кулі, то добування білої кулі з урни – достовірна подія, а добування з цієї урни кулі іншого кольору – неможлива подія. Якщо кинути монету на площину, то поява герба буде випадковою подією, тому що замість герба може з’явитися надпис. Елементарний наслідок випадкового експерименту – така подія, яка не може бути сумою інших наслідків цього ж експерименту. Множину всіх елементарних наслідків називають простором елементарних наслідків та експериментів. Простір елементарних наслідків може містити скінчену (злічену) або незлічену множину елементів. Приклад 1-1. А ={1} – елементарний наслідок B = {³ 4} C = {1; 3} D = {3} C = AÈD – неелементарний наслідок. Приклад 1-2.
Дати означення суми (обєднання), різниці та добутку (перетину) подій, протилежної події, повної групи подій. Навести приклади, дати означення сумісних, несумісних та попарно несумісних подій. Навести приклади. Сумою (об’єднанням) подій Різницею двох подій Добутком (перетином) подій Якщо події Якщо повну групу подій утворюють дві події, то вони називаються протилежними. Приклад 1-1. Влучення та промах при пострілі по цілі – протилежні події. Приклад 1-2. В ящику 30 куль: 10 червоних, 5 синіх та 15 білих. Знайти ймовірність появи кольорової кулі. Розв. Поява кольорової кулі означає появу або червоної, або синьої кулі. А – ймовірність появи червоної кулі, В – синьої. Р(А)=1/3, Р(В)=1/6. Події А та В несумісні, тому використовуємо теорему додавання: Р(А+В) = Р(А) + Р(В) = 1/3 + 1/6 = ½. Дві події А і В називають несумісними, якщо поява однієї з них виключає появу інших подій в одному і тому ж випробуванні. Дві події А і В називають сумісними, якщо поява однієї з них не виключає можливості появи інших. Події Приклад 1-1. Події «поява герба» та «поява напису» на кинутій монеті – несумісні. Приклад 1-2. При купівлі двох квитків лотереї обов’язково відбудеться тільки одне з наступних подій: «переміг 1 квиток та не переміг 2», «перемогли обидва квитки», «обидва квитки не перемогли». Ці події складають повну групу попарно-несумісних подій. Приклад 1-3. В урні декілька предметів різних форм та кольорів. Події «перший вийнятий навмання предмет квадратної форми» та «перший вийнятий навмання предмет рожевого кольору» - сумісні події. Дати означення поняття імовірності випадкової події. Сформулювати класичне визначення імовірності події і записати відповідну формулу. Навести приклади. Назвати основні фактори, що обмежують застосування класичного визначення імовірності. Сформулювати геометричне визначення імовірності. Навести приклад. Дати означення частоти та відносної частоти події. Ймовірність випадкової події є кількісна міра об’єктивної можливості появи цієї події. Класичне визначення ймовірності. Імовірність події А дорівнює відношенню числа елементарних наслідків, які сприяють появі події А, до загального числа усіх єдиноможливих та рівно можливих елементарних наслідків.
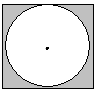
Де к – число елементарних наслідків, що сприяють події А, п – число усіх єдино можливих та рівно можливих наслідків. Якщо k=0, Р(А)=0 – ймовірність неможливої події. Якщо k=п, Р(А)=1 – ймовірність достовірної події. Прикла д: Серед 30 деталей у ящику 10 нестандартних. Ймовірність того, що навмання вийнята з ящику деталь – нестандартна Р = 10/30 = 1/3. Основні фактори, що обмежують застосування класичного визначення ймовірності. 1. рівноможливость всіх елементарних наслідків експерименту. 2. скінченность або зліченность простору елементарних наслідків. 3.можливость представлення подій, ймовірність яких треба обчислити, як суму елементарних наслідків. Геометричне визначення ймовірності. Імовірність випадкової події А дорівнює відношенню міри g до міри G
(може використовуватись у випадку, коли всі елементарні наслідки рівноможливі, але простір елементарних наслідків є незлічена множина, яка займає деяку область G). Нехай появі події А сприяє деяка її частина g, gÌG. Приклад. Є квадрат зі стороною а, у який вписане коло. В цей квадрат навмання кидають кулю. Знайти ймовірність того, що куля впаде за колом. Розв’язок. Нехай деякий експеримент, в результаті якого деяка подія А може з’явитися 1 раз (або не з’явитись) проводиться п раз і в m експериментах з’явилася 1 раз. Число m наз. частотою появи події А в п експериментах. Число W(A)=m/n називають відносною частотою появи події А. Тобто це відношення числа випробувань, у яких подія А з’явилась, до числа фактично виконаних випробувань. Оскільки випадкова подія має властивість статистичної стійкості, то W(A) із змінною числа п буде мало змінюватись, коливаючись біля деякого числа, яке і буде ймовірністю появи події А. Формула повної ймовірності
Формула Байєса:
де Приклад на Байєса: на фермах № 1 і № 2 відбулась спалах захворювання ящуром. Долі зараження 1/6 і 1/4. Випадково було відібрано із однієї ферми тварину, що захворіла. Знайти імовірність того, що ця тварина з першої ферми. Р (В/А)=(1/2*1/6)/(1/2*1/6+1/2*1/4)=0,4 Відповідь: 0,4. Приклад на повну імовірність: азотне добриво постачається з пунктів №1 і №2, при чому з першого пункта у 2р> ніж з другого.Імовірність події В1 (добриво з першого пункта задовольняє стандарт)=0,9, а відповідно імовірність для другого пункта=0,7. Знайти імовірність події А – взяте добриво відповідає стандарту. Р(В1)=2/3, Р(В2)=1/3 Р(А)= Р(В1)*0,9+Р(В2)*0,7=2/3*0,9+1/3*0,7=0,83 36. Дати означення генеральних та вибіркових дисперсії та середнього квадратичного відхилення. Записати формули для їх обчислення, пояснити зміст позначень. Навести приклади. Пояснити необхідність використання виправленої дисперсії та записати формулу її обчислення. Генеральною дисперсією DГ називають середнє арифметичне квадратів відхилень значень ознаки генеральної сукупності від їх середнього значення Якщо всі значення х1, х2,…хN ознаки генеральної сукупності об’єму N різні, то
Якщо значення ознаки х1, х2,…хk мають відповідно частоти N1, N2,…Nk, причому N1+ N2+…+Nk=N, то
Наприклад Генеральна сукупність задана таблицею розподілу хі 2 4 5 6 Ni 8 9 10 3 Знайти генеральну дисперсію. Розв’язання Знайдемо генеральну середню
Знайдемо генеральну дисперсію Генеральним середнім квадратичним відхиленням називають корінь квадратний із генеральної дисперсії σГ= Вибірковою дисперсією DВ називають середнє арифметичне квадратів відхилення спостерігаємих значень ознаки від їх середнього значення Якщо всі значення х1, х2,…хN ознаки генеральної сукупності об’єму n різні, то
Якщо значення ознаки х1, х2,…хk мають відповідно частоти n1, n2,…nk, причому n1+ n2+…+nk=n, то
Наприклад Вибіркова сукупність задана таблицею розподілу хі 1 2 3 4 ni 20 15 10 5 Знайти вибіркову дисперсію Знайдемо вибіркову середню Знайдемо вибіркову дисперсію Вибірковим середнім квадратичним відхиленням (стандартом) називають квадратний корінь із вибіркової дисперсії: σВ= Нехай із генеральної сукупності в результаті n незалежних спостережень над кількісною ознакою Х зроблена повторна вибірка об’єму n Значення ознаки……………………… х1 х2 … хk Частоти ………………………………. n1 n2 … nk причому n1+ n2+…+nk=n. Необхідно за даними вибірки оцінити невідому генеральну дисперсію DГ . якщо в якості оцінки генеральної дисперсії прийняти вибіркову дисперсію, то ця оцінка призводитиме до систематичних помилок, показуючи знижене значення генеральної дисперсії. Пояснюється це тим, що, як можна довести, вибіркова дисперсія є зміщеною оцінкою DГ, іншими словами, математичне сподівання вибіркової дисперсії не рівно оцінюємої генеральної дисперсії, а рівне Легко «виправити» вибіркову дисперсію так, щоб її математичне сподівання було рівне генеральній дисперсії. Для цього достатньо помножити Dв на дріб
Приклади. Модой называют варианту, которая имеет наибольшую частоту. При графічному способі зображення закону розподілу в.в., значення в.в. імовірність якого найбільша називають модою. Например, для ряда варианта….1 4 7 9 Частота… 5 1 20 6 Мода равна7. Медианой называют варианту.которая дельт вариационный ряд на 2 части, равные по числу вариант. Например для ряда, 2 3 5 6 7 медиана равна 5. Початковым моментом порядку к. в. в. Х називають математичне сподівання величини Хк і позначають Центральнім моментом порядку к.в.в. Х наз. математичне сподівання величини і позначають Асиметріею або коефіцієнтом асиметрії називається величина - центральній момент третього порядку - середне квадратичне відхилення. Якщо Аs =0 (Аs=0), то розподіл симетричний(асиметричний); Якщо Аs >0 (Аs<0), то асиметрія правостороння (лівостороння). Ексцес в.в. характеризує плосковерхість чи гостроверхість розподілу, порівняно з нормативним розподілом з тим же значенням дисперсії.
Якщо Ех >0 (Ex<0),то розподіл гостроверхній (плосковерхній) 45.Навести основні властивості кореліаційного моменту та коефіцієнту кореляції. Дати означення корельованості(некорельованості) двохв.в. пояснити різницю і зв'язок між корельованістю(некорельованістю) і залежністю (незалежністю) двох в.в. Корреллиационный момент служит для характеристики связи между величинами X и Y. М равен нулю, если X и Y независимы, следовательно, если М не равен нулю, то X и Y- зависимые случайные величины. Величина коэф.корел. не зависит от выбора единицы измерения случайных величин. В этом состоит преимущество коэф.корел. перед кореллиационным моментом КК независимых случайных величин X и Y не превышает среднего геометрического их дисперсий, абсолютная величина не превышает еденицы. Властивості кор.. моменту:1) кор. Момент 2 незалежних в.в.X та Y=0. І навпаки, якщо кор. Момент не рівний 0, то X та Y-залежні в.в.2) абсолютна величина кор.моменту 2 в.в.X та Y не перевищує середнього геометричного їх дисперсій. Властивості коеф.кореляції:1){rxy}<=1; 2)якщо X та Y незалежні, то rxy=0;3) якщо між X та Y є лінійна залежність Y=a×X+b- сталі, то {rxy}=1. Корельованими наз. 2 d/d/?zroj їх µxy відрізняється від 0. Некорельованим наз. 2 d/d/?zroj їх µxy=0. Две случайные величины X и Y наз. Корел.,если их корел.момент отличен от нуля, X и Y называют некор.величинами, если их кор.момент равен нулю. Две кор.величины,если их кор.момент равен 0. Две кор.величины также и зависимы. Зв'язок між корел-ю (некорел-ю) та залежністю: якщо X,Y, некорельовані µxy=0, то залежність невідома; якщо X,Y корельовано, то вони залежні; якщо X, Y незалежні, то вони некорельовані X, Y=0; якщо X, Y залежні, то вони можуть бути як корельованими так і декор. µxy-індикатор залежності і незалежності X, Y. Різниця: із незалежності 2 величин слідує їх некорельованість,але із некорельованості не можна зробити висновок про незалежність цих величин. Що в теорії ймовірностей розуміють під терміном «Закон великих чисел»? Записати нерівність А. Чебишова. Пояснити зміст букв. Граничні теореми теорії ймовірностей встановлюють відповідність між теоретичними та дослідними характеристиками випадкових величин або випадкових подій при великій кількості випробувань. Граничні теореми описують також граничні закони розподілу. Граничні теореми, які встановлюють відповідність між теоретичними та дослідними характеристиками випадкових подій, об’єднують загальною назвою – закона великих чисел. Перша форма нерівності Чебишова. Для довільної випадкової величини Х, яка приймає невід’ємні значення та має скінчене математичне сподівання Р(Х≥1)≤М(Х). Якщо Х – дискретна випадкова величина, то Р(Х≥1) = Якщо Х – неперервна випадкова величина, f(x) – щільність її імовірностей, то
Р(Х≥1) = Друга форма нерівності Чебишова. Якщо випадкова величина Х має скінчені математичне сподівання та дисперсію, то для довільного ε>0 має місце нерівність
|
||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.90 (0.008 с.) |


 .
.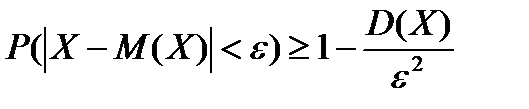
 називають сукупність умовних імовірностей
називають сукупність умовних імовірностей  │
│ 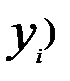 ,
,  │
│ 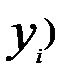 ,….
,…. 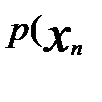 │
│  - (1)
- (1)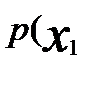 ,
,  -(2)
-(2) -(3)
-(3)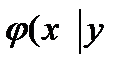 ) розпреділення складаючих Х при даному значенні Y=y називають відношення щільності совмесному розпреділенню f(x,y) системи (X,Y) до щільності
) розпреділення складаючих Х при даному значенні Y=y називають відношення щільності совмесному розпреділенню f(x,y) системи (X,Y) до щільності 
 складової Y:
складової Y: . Підкреслимо,що відмінність умовної щільність
. Підкреслимо,що відмінність умовної щільність 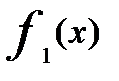 состоит в том що функція
состоит в том що функція  .
.
 - це спосіб завдання множини перерахуванням скінченної множини
- це спосіб завдання множини перерахуванням скінченної множини - це спосіб завдання перерахуванням нескінченної множини;
- це спосіб завдання перерахуванням нескінченної множини;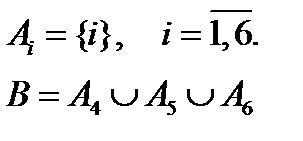 - злічена множина елементів.
- злічена множина елементів. наз. Таку подію В, яка полягає в тому, що настане хоча б одна з подій Аі.
наз. Таку подію В, яка полягає в тому, що настане хоча б одна з подій Аі. -
- 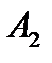 наз. Усі наслідки, які полягають в тому, що настане подія А1 та не настане подія А2.
наз. Усі наслідки, які полягають в тому, що настане подія А1 та не настане подія А2. , і
, і  , і …, і
, і …, і  одночасно.
одночасно.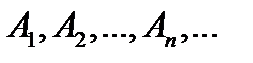 попарно-несумісні і їх об’єднання є достовірною подією, то вони утворюють повну групу подій.
попарно-несумісні і їх об’єднання є достовірною подією, то вони утворюють повну групу подій.


 , де
, де  - ймовірність появи події А,
- ймовірність появи події А,  - ймовірність появи події
- ймовірність появи події  ,
,  - ймовірність появи події А при умові, що перед тим з’явиться подія
- ймовірність появи події А при умові, що перед тим з’явиться подія 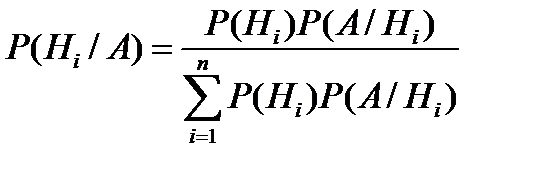 ,
,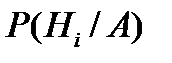 - ймовірність гіпотези
- ймовірність гіпотези  після проведення експерименту, в результаті якого з’явилась подія А.
після проведення експерименту, в результаті якого з’явилась подія А.  - ймовірність гіпотези
- ймовірність гіпотези  - гіпотези А після проведення експерименту, в результаті якого з’явилась подія
- гіпотези А після проведення експерименту, в результаті якого з’явилась подія  .
. .
. , тобто генеральна дисперсія є середньою зваженою квадратів відхилень із вагами, рівними відповідним частотам.
, тобто генеральна дисперсія є середньою зваженою квадратів відхилень із вагами, рівними відповідним частотам.


 .
.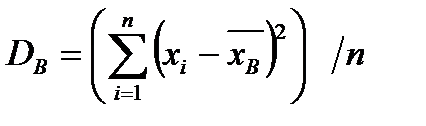
 . Отже, тобто вибіркова дисперсія є середньою зваженою квадратів відхилень із вагами, рівними відповідним частотам.
. Отже, тобто вибіркова дисперсія є середньою зваженою квадратів відхилень із вагами, рівними відповідним частотам.

 .
. .
. .Зробивши це, ми отримаємо виправлену дисперсію, яку зазвичай позначають через S2.
.Зробивши це, ми отримаємо виправлену дисперсію, яку зазвичай позначають через S2.



