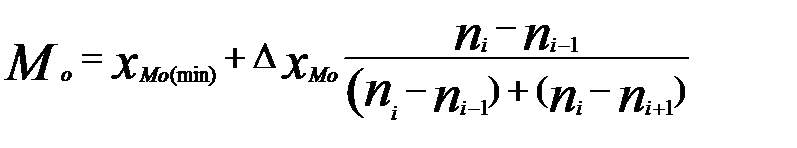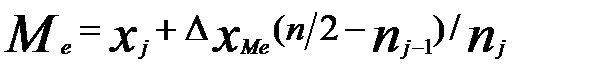Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистичні критерії та областіСодержание книги
Поиск на нашем сайте
1. Статистичний критерій – випадкова величина К, розподіл якої (точний або наближений) відомий і яка застосовується для перевірки основних гіпотези Якщо статистична характеристика розподілена: - нормально,то критерій позначають не К, а літерами U або Z - за законом Фішера-Снедекора, то F - за законом Стьюдента, то Т - за законом «Xi-квадрат», то 2. Спостереженим значенням критерію узгодження називають значення відповідного критерію, обчислене за даними вибірки. 3. Критчною областю називають сукупність значень критерію, при яких основа гіпотеза відхиляється. 4. Областю прийняття гіпотези (областю допустимих значень) називають множину значень критерію, при яких гіпотезу приймають. 5. Критичними точками (межами) критерію К називають точки «Ккр», які відокремлюють критичну область від області прийняття гіпотези. 6. Розрізняють однобічну (правобічну та лівобічну) та двобічну критичні області. Правобічною називають критичну область, що визначається нерівністю К>Ккр, де Ккр – додатне число. Лівобічною називають критичну область, що визначається нерівністю К<Ккр, де Ккр – відємне число.
Дати означення умовного закону розподілу складових системи д.в.в. Записати формули для обчислення умовних ймовірностей складових систем д.в.в. Пояснити зміст позначень. Дати означення умовної щільності імовірностей складових системи н.в.в.
Умовним розпреділенням складаючий Х при У=
Умовна щільність
Питання №9 ЗАЛЕЖНІСТЬ/НЕЗАЛЕЖНІСТЬ ВИПАДКОВИХ ВЕЛИЧИН Незалежні – якщо закон розподілу однієї з двох випадкових величин не залежить від того, які можливі значення прийняла друга величина. Залежні – якщо закон розподілу однієї з двох випадкових величин залежить від того, які можливі значення прийняла друга величина.
Теорема: Щоб випадкові величини Х та У були незалежні, необхідно і достатньо, щоб інтегральна функція системи (Х,У) дорівнювала добутку інтегральних функцій кожної з них F(x,y)=F1(x)*F2(y) Наслідок: Щоб неперервні випадкові величини Х та У були незалежними, необхідньо і достатньо, щоб диференціальна фунцкія системи (Х,У) дорівнювала добутку дифферинціальних фунцкій складових f(x,y)=f1(x)*f2(y) 10. Дати означення основних числових характеристик в.в.: а) М(х); б)D(x); в) початкового та центрального моментів; г)асиметрії; д)ексцесу; е) моди; ж)медіани. Записати формули для їх обчислень для д.в.в. та н.в.в. М(х)-називають число, яке дорівнює сумі добутків усіх можливих значень Х на відповідні їм імовірності. М(х) = М(х)= D(x)-називають число, яке =математичному сподіванню квадрата відхилення ДВВ Х від її математичного сподівання. D(x)=M((X-M( D(x)= D(x)= Почаковим моментом порядку k випадкової величини Х називають математичне сподівання величини
Центральним моментом- порядка k випадкової величини Х називають М(Х) величини (Х-М(
Асиметрія-це скошеність графіка і залежить від коефіцієнта g. Якщо g>0 то буде лівостороння скошеність, якщо g<0 то правостороння скошеність. g=
Ексцес-це показник гостровершинності. Якщо E>0 то полігон гостровершний, а якщо E<0 то плосковершний. g=
Мода- називається варіанта, яка найбільш часто зустрічається в даному варіаційному ряді
Медіана- варіанта, яка розділяє дискретний варіаційний ряд на 2 частини, рівні між собою за числом варіант.
|
||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.95 (0.005 с.) |

 називають сукупність умовних імовірностей
називають сукупність умовних імовірностей  │
│ 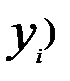 ,
,  │
│ 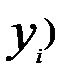 ,….
,…. 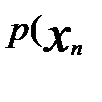 │
│  - (1)
- (1)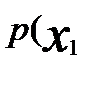 ,
,  -(2)
-(2) -(3)
-(3)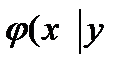 ) розпреділення складаючих Х при даному значенні Y=y називають відношення щільності совмесному розпреділенню f(x,y) системи (X,Y) до щільності
) розпреділення складаючих Х при даному значенні Y=y називають відношення щільності совмесному розпреділенню f(x,y) системи (X,Y) до щільності 
 складової Y:
складової Y: . Підкреслимо,що відмінність умовної щільність
. Підкреслимо,що відмінність умовної щільність 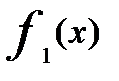 состоит в том що функція
состоит в том що функція  .
.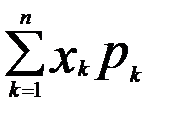 -для ДВВ
-для ДВВ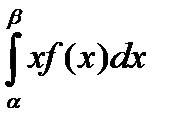 -для НВВ
-для НВВ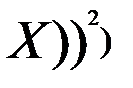 -для ДВВ
-для ДВВ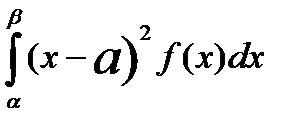 -для НВВ
-для НВВ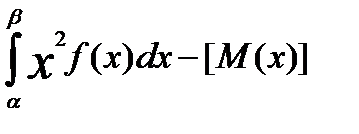
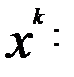
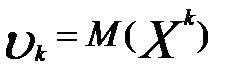
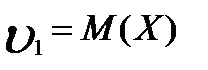 ,
, 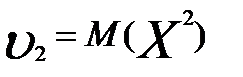 або
або 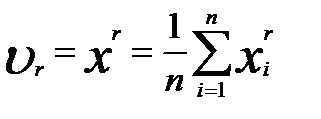
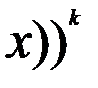
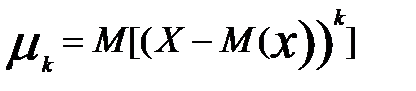 або
або 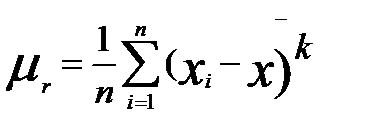
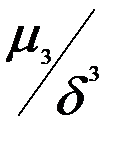
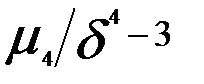
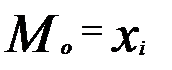 . Для НВВ за моду іноді беруть серединне значення напівсигмента.
. Для НВВ за моду іноді беруть серединне значення напівсигмента.