
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дати означення рівня значущості та потужності статистичного критерію. Пояснити способи знаходження одностороньої та двустороньої областей, імовірностний зміст рівня значущості.Содержание книги
Поиск на нашем сайте Статистичним критерієм називають випадкову величину К, яка застосовується для перевірки гіпотези. Напиклад, якщо поревіряють гіпотезу про рівність дисперсій двох гернеральних сукупностей, то в якості критерію приймають відношення:
Спостережуваним значенням Кспост називають те значення критерію, яке обчислене по вибіркам. Наприклад, S2 i =20, S2 i =5,то F=20/5. Критичною областю називають такі значення критерія, при яких відкидають нульову гіпотезу. Областю прийняття гіпотези називають сукупність значення критерія, при якій нульову гіпотезу приймають. Критичними точками kкр називають точки, що відділяють критичну область від області прийняття гіпотези. Правосторонньою (Лівосторонньою) критичною областю називають область, що визначається нерівністю K> (<) kkr, де ккр – додатнє (від‘ємне) число. Двосторонньою називають область, яка визначається нерівностями: К>k1, K<k2; при цьому k2>k1. Досить малу ймовірність, при якій (у даній певній задачі) подія можна вважати практично неможливим, називають рівнем значимості. На практиці звичайно приймають рівні значимості, укладені між 0,01 і 0,05. Потужністю критерію називають вірогідність попадання критерію в критичну область за умови, що справедлива конкуруюча гіпотеза. Іншими словами, потужність критерію є вірогідність того, що нульова гіпотеза буде знехтувана, якщо вірна конкуруюча гіпотеза. Однобічної називають правобічну або лівосторонню критичну область. Двосторонньої називають критичну область, обумовлену нерівностями K<k1 K>k2, де k2> k1 Зокрема, якщо критичні крапки симетричні відносно нуля двостороння критична область визначається нерівностями (у припущенні; що k kp>0): Дати означення сполучення та розміщення із n елементів по k, переставлення із n елементів. Записати позначення та формули для обчислення числа цих сполук. Навести приклади. Розміщенням із n елементів по k називається упорядкована k-елементна підмножина n-елементної множини.
Переставленням із n елементів називається розміщення із m елементів по n.
Сполученням із n елементів по k називається будь-яка неупорядкована k-елементна підмножина n-елементної множини.
Приклад 1-1. Скількома способами можна розсадити 4 учнів на 25 місцях? Шукане число дорівнює числу розміщень з 25 по 4: Приклад 1-2. Скількома способами можна розташувати на полиці 4 книги (позначимо їх А, В, С, D)? Шукане число способів дорівнює числу способів упорядкування множини, що складається з 4 елементів, тобто Приклад 1-3. Кості доміно можна розглядати як комбінації з повтореннями по два з семи цифр 0, 1, 2, 3, 4, 5, 6. Число всіх таких комбінацій дорівнює Дати означення випадкового експерименту, випадкової події, неможливої та достовірної подій. Навести приклади. Дати означення елементарного наслідку випадкового експерименту, простору елементарних наслідків. Експеримент (випробування) – реалізація певної сукупності умов, в результаті якої настає певна подія. Експеримент наз. випадковим, якщо в результаті його проведення може настати деяка подія. Випадковою називають таку подію, яка при умовах, що розглядаються,може трапитися, а може й не трапитися. Неможливою називають таку подію, яка при розглянутих умовах не може трапитися. Достовірною називають таку подію, яка при розглянутих умовах обов’язково трапиться. Приклади: Якщо в урні є лише білі кулі, то добування білої кулі з урни – достовірна подія, а добування з цієї урни кулі іншого кольору – неможлива подія. Якщо кинути монету на площину, то поява герба буде випадковою подією, тому що замість герба може з’явитися надпис. Елементарний наслідок випадкового експерименту – така подія, яка не може бути сумою інших наслідків цього ж експерименту. Множину всіх елементарних наслідків називають простором елементарних наслідків та експериментів. Простір елементарних наслідків може містити скінчену (злічену) або незлічену множину елементів. Приклад 1-1. А ={1} – елементарний наслідок B = {³ 4} C = {1; 3} D = {3} C = AÈD – неелементарний наслідок. Приклад 1-2.
|
||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.147.141 (0.007 с.) |


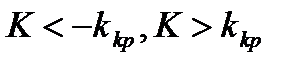 або рівносильною нерівністю
або рівносильною нерівністю 




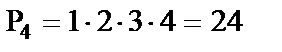 .
.
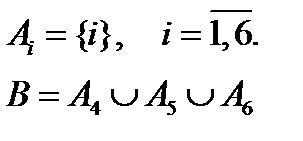 - злічена множина елементів.
- злічена множина елементів.


