
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Випадкові процеси та їх основні статистичні характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Величина
являє собою ймовірність того, що X(t) знаходиться на момент часу t = t1 в інтервалі від х 1 до х 1 + dx1. Прикладом випадкового процесу, що повністю характеризується одномірною щільністю ймовірності, є так званий білий шум. Значення X(t) у цьому процесі, взяті на різні моменти часу t, цілковито незалежні одне від одного, як би близько не були вибрані ці моменти часу. Це означає, що крива білого шуму містить викиди, що затухають за нескінченно малі проміжки часу. Функції F1(x, t) і w1(x, t) є простішими статистичними характеристиками випадкового процесу. Вони характеризують випадковий процес ізольовано в окремих його перерізах, не розкриваючи взаємного зв’язку між перерізами випадкового процесу, тобто між можливими значеннями випадкового процесу на різні моменти часу. Знання цих функцій ще недостатньо для опису випадкового процесу в загальному випадку. Необхідно охарактеризувати також взаємний зв’язок випадкових величин на різні моменти часу. Розглянемо тепер випадкові величини X(t1) і X(t2), що належать до двох різних моментів часу t1 і t2 спостереження випадкового процесу. Ймовірність того, що X(t) буде не більше х 1 при t=t1 і не більше х 2 при t=t2, тобто
називають двомірною функцією розподілу (функцією розподілу другого порядку). Якщо функція F2(x1, t1; x2, t2) має частинні похідні за х 1 і х 2, тобто:
то функцію w2(x1, t1; x2, t2) називають двомірною щільністю ймовірності (щільністю ймовірності другого порядку) випадкового процесу. Величина
являє собою ймовірність того, що X(t) знаходиться на момент часу t = t1 в інтервалі від х 1 до х 1 + dx1, а на момент часу t = t2 - в інтервалі від х 2 до х 2 + dx2. Двомірною щільністю ймовірності (12.7) повністю характеризуються так звані марковські випадкові процеси (за ім’ям відомого математика, академіка Петербурзької АН Андрія Андрійовича Маркова, який уперше дослідив ці процеси), для яких знання значення процесу на момент часу tk містить усю можливу інформацію про подальший хід процесу. Аналогічно можна ввести поняття про n -мірну функцію розподілу і n -мірну щільність ймовірності. Чим вище порядок n, тим повніше описуються статистичні властивості випадкового процесу, але багатомірні закони розподілу є громіздкими і незручними для використання. Тому частіше обмежуються випадками, коли для опису випадкового процесу достатньо знати тільки одномірний чи двомірний закон розподілу. У практиці досліджень систем автоматичного керування широке розповсюдження отримали порівняно більш прості, хоча й менш повні характеристики випадкових процесів, аналогічні числовим характеристикам випадкових величин: математичне сподівання, дисперсія, середнє значення квадрата випадкового процесу, кореляційна функція, спектральна щільність та інші. Математичним сподіванням (середнім значенням) mx(t) випадкового процесу X(t) називають величину:
де w1(x, t) – одномірна щільність ймовірності випадкового процесу X(t). Математичне сподівання випадкового процесу X(t) являє собою деяку невипадкову (регулярну) функцію часу mx(t), біля якої групуються і відносно якої коливаються всі реалізації даного випадкового процесу. Математичне сподівання називають середнім значенням випадкового процесу за множиною (статистичним середнім), оскільки воно являє собою ймовірносно усереднене значення нескінченної множини реалізацій випадкового процесу. Середнім значенням квадрата випадкового процесу називають величину:
Часто розглядають так званий центрований випадковий процес
Тоді випадковий процес X(t) можна розглядати як суму двох складових: регулярної складової, що дорівнює математичному сподіванню mx(t), і центрованої випадкової складової
Зрозуміло, що математичне сподівання центрованого випадкового процесу дорівнює нулю:
Для того, щоб урахувати ступінь розкидання реалізацій випадкового процесу відносно його середнього значення, застосовують поняття дисперсії випадкового процесу, яка дорівнює математичному сподіванню квадрата центрованого випадкового процесу:
Дисперсія випадкового процесу є невипадковою (регулярною) функцією Dx(t), значення якої на кожний момент часу tk дорівнює дисперсії відповідного перерізу X(tk) випадкового процесу. Математичне сподівання mx(t), дисперсія Dx(t) і середнє значення квадрата
Із (12.15) видно, що середнє значення квадрата випадкового процесу Іноді зручно використовувати статистичні характеристики випадкового процесу, які мають ту саму розмірність, що й сама випадкова величина: - середнє квадратичне значення випадкового процесу:
що дорівнює арифметичному значенню квадратного кореня із середнього значення квадрата випадкового процесу; - середнє квадратичне відхилення випадкового процесу:
що дорівнює арифметичному значенню квадратного кореня із дисперсії випадкового процесу. Характеристику (12.17) використовують тільки для центрованих випадкових процесів. Знання вказаних вище статистичних характеристик часто є достатнім для розв’язання багатьох задач теорії автоматичного керування.
Рівняння Вінера-Хопфа Це рівняння встановлює зв’язок між кореляційними функціями вхідного X(t) і вихідного Y(t) сигналів, що діють у лінійній динамічній системі. Відповідно до (12.28) взаємна кореляційна функція цих сигналів має вигляд:
Тоді з урахуванням (12.51) запишемо:
Цей вираз має назву рівняння Вінера-Хопфа. Застосувавши до інтегрального рівняння (12.59) пряме перетворення Фур’є, можна записати: Syx(w) = W(jw)Sx(w) або W(jw) = Syx(w) / Sx(w), (12.60) де Syx(w) і Sx(w) – взаємна і власна спектральні щільності. Застосовуючи до (12.60) обернене перетворення Фур’є, маємо:
Рівняння (12.60) і (12.61) дозволяють знайти динамічні характеристики системи W(jw) і w(t) за відомими імовірнісними характеристиками входу X(t) і виходу Y(t), що визначаються за реалізаціями випадкового процесу.
Квадратичною помилкою
Система повинна якомога точніше відтворювати на своєму виході не саму керуючу дію Х(t), а деяку функцію від неї: Z(t) = H(p)X(t). (12.75) У системах, що знаходяться під впливом випадкового (або регулярного) корисного сигналу і випадкового збурення, виникає задача відділення корисного сигналу від перешкоди та фільтрації цієї перешкоди. Цю задачу називають задачею фільтрації або згладжування. Уведення перетворюючого оператора Н(р) узагальнює задачу не тільки на слідкуючі системи, у яких Z(t) = X(t) (тобто Н(Р) = 1), але й на інші класи систем, що виконують різні перетворювання керуючого сигналу. Залежно від вигляду оператора Н(р) задача фільтрації поєднується із задачею відтворювання (якщо Н(р) = const), випередження або екстраполяції, інтегрування, диференціювання тощо. У загальному випадку оператор Н(р) може бути довільним. Через динамічні помилки системи, а також наявність перешкод, вихідний сигнал Y(t) буде відрізнятися від сигналу Z(t). Різницю E(t) = Z(t) – Y(t) (12.76) називають випадковою помилкою системи. Синтез систем при випадкових впливах полягає у визначенні динамічних характеристик системи, що найкращим чином забезпечують виконання деякого статистичного критерію оптимальності. Найчастіше як такий критерій беруть критерій мінімуму середньої квадратичної помилки (див. 12.69):
де e(t) – будь-яка реалізація випадкової помилки. У цьому випадку задача синтезу полягає у тому, щоб знайти таку оптимальну передавальну функцію замкнутої системи Wз.опт.(р), яку можна фізично реалізувати, і при якій середнє значення квадрата помилки
Використання даного статистичного критерію може бути нераціональним у тих випадках, коли вимоги до величини помилки на різні моменти часу неоднакові, але через свою простоту він набув широкого практичного застосування. Способи розв’язування задачі синтезу при випадкових діях можуть бути різними залежно від вигляду графіка спектральної щільності керуючого сигналу і збурення. У найпростішому випадку, коли спектри частот корисного сигналу Sx(w) і збурення Sf(w) не накладаються один на одного (рис. 12.6, а) АЧХ замкнутої системи А(w) вибирають достатньо широкою для забезпечення необхідної точності відтворювання керуючого сигналу й водночас достатньо вузькою, щоб система менше реагувала на перешкоду. Якщо керуючий сигнал має спектр частот, що швидко убуває зі зростанням частоти, а спектр завад є близьким до білого шуму (рис. 12.6, б), то форму АЧХ |W(jw)| розімкнутої системи слід вибирати на низьких частотах, де |W(jw)| >> 1 і де сконцентрована основна енергія керуючого сигналу, якомога близькою до форми спектральної щільності керуючого сигналу Sx(w). У загальному випадку, коли спектри частот корисного сигналу й перешкоди накладаються і мають довільну форму (рис. 12.6, в) визначення оптимальних параметрів системи стає достатньо складним.
Під час синтезу систем із випадковими впливами розрізняють два види задач: - синтез при заданій структурі системи керування, коли намагаються досягти мінімуму середньої квадратичної помилки за рахунок вибору оптимальних параметрів коректувальних ланок системи на підставі відомих статистичних характеристик корисного сигналу і збурення; - синтез при довільній структурі системи керування, коли за відомими статистичними характеристиками корисного сигналу і збурення визначають оптимальну структуру і параметри системи, що забезпечують мінімум середньої квадратичної помилки. Випадкові процеси та їх основні статистичні характеристики Функція, значення якої при кожному значенні незалежної змінної є випадковою величиною, називається випадковою функцією. Випадкові функції, для яких змінною є час t, називають випадковими процесами або стохастичними процесами. Якщо, наприклад, проведено n окремих випробувань, то у результаті випадковий процес X(t) може набути n різних невипадкових (регулярних) функцій часу xi(t), де і = 1, 2,..., n. Будь-яка з цих функцій xi(t), якій виявився рівним випадковий процес X(t) у результаті випробування, називається реалізацією випадкового процесу (або можливим значенням випадкового процесу). Сказати наперед, за якою з реалізацій піде процес, неможливо. Розглянемо, наприклад, випадковий дрейф на виході підсилювача постійного струму при вхідній напрузі, що дорівнює нулю. Щоб вивчити характеристики дрейфу, можна взяти n однакових підсилювачів, помістити їх у однакові умови роботи, одночасно ввімкнути і отримати n осцилограм дрейфу на виходах підсилювачів. Кожна з осцилограм є конкретною реалізацією xi(t) випадкового процесу X(t). Для будь-якого фіксованого моменту часу t = t1 реалізація випадкового процесу xi(t1) є конкретною величиною, а значення випадкової функції X(t1) є випадковою величиною, що називається перерізом випадкового процесу на момент часу t1. Тому не можна стверджувати, що випадковий процес на даний момент часу має деяке детерміноване значення, можна говорити лише про ймовірність того, що на даний момент часу значення випадкового процесу, як випадкової величини, буде знаходитись у певних границях. Статистичні методи вивчають не кожну з реалізацій xi(t), що утворюють множину X(t), а властивості всієї множини у цілому. Тому під час дослідження автоматичної системи керування роблять висновок про її поведінку не відносно будь-якого певного впливу, а відносно цілої сукупності впливів. Статистичні властивості випадкової величини х визначають за її функцією розподілу (інтегральним законом розподілу) F(x) або за щільністю ймовірності (диференціальним законом розподілу) w(x). Випадкові величини можуть мати різні закони розподілу: рівномірний, нормальний, експоненціальний тощо. У багатьох задачах автоматичного керування дуже часто використовують нормальний закон розподілу (закон Гаусса), який має місце, якщо випадкова величина визначається сумарним ефектом від впливу великої кількості різних незалежних факторів. З курсу теорії ймовірності відомо, що випадкова величина х при нормальному законі розподілу повністю визначається математичним сподіванням (середнім значенням) mx і середнім квадратичним відхиленням sх. Аналітичний вираз функції розподілу в цьому випадку має вигляд:
Аналітичний вираз щільності ймовірності для нормального закону розподілу:
Для випадкового процесу використовують також поняття функції розподілу F(x, t) і щільності ймовірності w(x, t), що залежать від фіксованого моменту часу t і від деякого вибраного рівня х, тобто є функціями двох змінних: х і t. Розглянемо випадкову величину X(t1), тобто переріз випадкового процесу на момент часу t1. Одномірною функцією розподілу (функцією розподілу першого порядку) випадкового процесу X(t) називають ймовірність того, що поточне значення випадкового процесу X(t1) на момент часу t1 не перевищує деякого заданого рівня (числа) х 1, тобто:
Якщо функція F1(x1, t1) має частинну похідну за х 1, тобто:
то функцію w1(x1, t1) називають одномірною щільністю ймовірності (щільністю ймовірності першого порядку) випадкового процесу. Величина
являє собою ймовірність того, що X(t) знаходиться на момент часу t = t1 в інтервалі від х 1 до х 1 + dx1. Прикладом випадкового процесу, що повністю характеризується одномірною щільністю ймовірності, є так званий білий шум. Значення X(t) у цьому процесі, взяті на різні моменти часу t, цілковито незалежні одне від одного, як би близько не були вибрані ці моменти часу. Це означає, що крива білого шуму містить викиди, що затухають за нескінченно малі проміжки часу. Функції F1(x, t) і w1(x, t) є простішими статистичними характеристиками випадкового процесу. Вони характеризують випадковий процес ізольовано в окремих його перерізах, не розкриваючи взаємного зв’язку між перерізами випадкового процесу, тобто між можливими значеннями випадкового процесу на різні моменти часу. Знання цих функцій ще недостатньо для опису випадкового процесу в загальному випадку. Необхідно охарактеризувати також взаємний зв’язок випадкових величин на різні моменти часу. Розглянемо тепер випадкові величини X(t1) і X(t2), що належать до двох різних моментів часу t1 і t2 спостереження випадкового процесу. Ймовірність того, що X(t) буде не більше х 1 при t=t1 і не більше х 2 при t=t2, тобто
називають двомірною функцією розподілу (функцією розподілу другого порядку). Якщо функція F2(x1, t1; x2, t2) має частинні похідні за х 1 і х 2, тобто:
то функцію w2(x1, t1; x2, t2) називають двомірною щільністю ймовірності (щільністю ймовірності другого порядку) випадкового процесу. Величина
являє собою ймовірність того, що X(t) знаходиться на момент часу t = t1 в інтервалі від х 1 до х 1 + dx1, а на момент часу t = t2 - в інтервалі від х 2 до х 2 + dx2. Двомірною щільністю ймовірності (12.7) повністю характеризуються так звані марковські випадкові процеси (за ім’ям відомого математика, академіка Петербурзької АН Андрія Андрійовича Маркова, який уперше дослідив ці процеси), для яких знання значення процесу на момент часу tk містить усю можливу інформацію про подальший хід процесу. Аналогічно можна ввести поняття про n -мірну функцію розподілу і n -мірну щільність ймовірності. Чим вище порядок n, тим повніше описуються статистичні властивості випадкового процесу, але багатомірні закони розподілу є громіздкими і незручними для використання. Тому частіше обмежуються випадками, коли для опису випадкового процесу достатньо знати тільки одномірний чи двомірний закон розподілу. У практиці досліджень систем автоматичного керування широке розповсюдження отримали порівняно більш прості, хоча й менш повні характеристики випадкових процесів, аналогічні числовим характеристикам випадкових величин: математичне сподівання, дисперсія, середнє значення квадрата випадкового процесу, кореляційна функція, спектральна щільність та інші. Математичним сподіванням (середнім значенням) mx(t) випадкового процесу X(t) називають величину:
де w1(x, t) – одномірна щільність ймовірності випадкового процесу X(t). Математичне сподівання випадкового процесу X(t) являє собою деяку невипадкову (регулярну) функцію часу mx(t), біля якої групуються і відносно якої коливаються всі реалізації даного випадкового процесу. Математичне сподівання називають середнім значенням випадкового процесу за множиною (статистичним середнім), оскільки воно являє собою ймовірносно усереднене значення нескінченної множини реалізацій випадкового процесу. Середнім значенням квадрата випадкового процесу називають величину:
Часто розглядають так званий центрований випадковий процес
Тоді випадковий процес X(t) можна розглядати як суму двох складових: регулярної складової, що дорівнює математичному сподіванню mx(t), і центрованої випадкової складової
Зрозуміло, що математичне сподівання центрованого випадкового процесу дорівнює нулю:
Для того, щоб урахувати ступінь розкидання реалізацій випадкового процесу відносно його середнього значення, застосовують поняття дисперсії випадкового процесу, яка дорівнює математичному сподіванню квадрата центрованого випадкового процесу:
Дисперсія випадкового процесу є невипадковою (регулярною) функцією Dx(t), значення якої на кожний момент часу tk дорівнює дисперсії відповідного перерізу X(tk) випадкового процесу. Математичне сподівання mx(t), дисперсія Dx(t) і середнє значення квадрата
Із (12.15) видно, що середнє значення квадрата випадкового процесу Іноді зручно використовувати статистичні характеристики випадкового процесу, які мають ту саму розмірність, що й сама випадкова величина: - середнє квадратичне значення випадкового процесу:
що дорівнює арифметичному значенню квадратного кореня із середнього значення квадрата випадкового процесу; - середнє квадратичне відхилення випадкового процесу:
що дорівнює арифметичному значенню квадратного кореня із дисперсії випадкового процесу. Характеристику (12.17) використовують тільки для центрованих випадкових процесів. Знання вказаних вище статистичних характеристик часто є достатнім для розв’язання багатьох задач теорії автоматичного керування.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.61 (0.009 с.) |

 (12.5)
(12.5)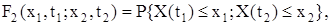 (12.6)
(12.6)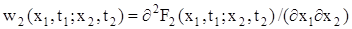 , (12.7)
, (12.7) (12.8)
(12.8) (12.9)
(12.9) (12.10)
(12.10) - відхилення випадкового процесу X(t) від його середнього значення mx(t):
- відхилення випадкового процесу X(t) від його середнього значення mx(t): (12.11)
(12.11) (12.12)
(12.12) (12.13)
(12.13)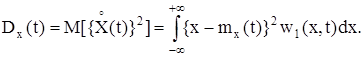 (12.14)
(12.14) випадкового процесу зв’язані співвідношенням:
випадкового процесу зв’язані співвідношенням: (12.15)
(12.15) (12.16)
(12.16) (12.17)
(12.17)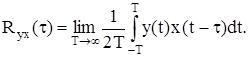 (12.58)
(12.58) (12.59)
(12.59) . (12.61)
. (12.61)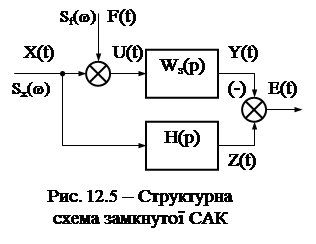 Розглянемо систему автоматичного керування з передавальною функцією Wз(р), яка слугує для підсилення й перетворення керуючого корисного сигналу Х(t) за наявності випадкового збурення F(t). Це перетворення у загальному випадку виконується відповідно до деякого заданого алгоритму перетворення H(p) (рис. 12.5).
Розглянемо систему автоматичного керування з передавальною функцією Wз(р), яка слугує для підсилення й перетворення керуючого корисного сигналу Х(t) за наявності випадкового збурення F(t). Це перетворення у загальному випадку виконується відповідно до деякого заданого алгоритму перетворення H(p) (рис. 12.5). (12.77)
(12.77) набувало б мінімуму:
набувало б мінімуму: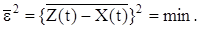 (12.78)
(12.78)
 (12.1)
(12.1) (12.2)
(12.2)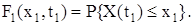 (12.3)
(12.3) (12.4)
(12.4)


