
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проходження випадкового сигналу крізь лінійну системуСодержание книги
Поиск на нашем сайте
Розглянемо стійку стаціонарну лінійну систему автоматичного керування з передавальною функцією W(s) й імпульсною перехідною функцією w(t). Припустимо, що на вхід цієї системи надходить стаціонарний випадковий процес X(t) із середнім значенням, що дорівнює нулю, кореляційною функцією Rx(t) і спектральною щільністю Sx(w). Усталений вихідний сигнал Y(t) також буде стаціонарним випадковим процесом, середнє значення якого дорівнює нулю, однак, його статистичні характеристики Rу(t) і Sу(w) будуть відрізнятися від статистичних характеристик вхідного сигналу. Зв’язок між кореляційними функціями вхідного і вихідного сигналів можна визначити за допомогою інтеграла Дюамеля (1.10):
де l - незалежна змінна інтегрування. Для моменту часу (t + t) отримуємо:
де h - нове позначення незалежної змінної інтегрування. Кореляційна функція стаціонарного випадкового процесу на підставі (12.24) дорівнює:
Підставивши до (12.53) вирази (12.51) і (12.52), після перетворень отримаємо шукану залежність:
Вираз (12.54) дозволяє за відомою кореляційною функцією Rx(t) випадкового процесу на вході системи і відомою імпульсною перехідною функцією w(t) системи знайти кореляційну функцію Rу(t) випадкового процесу на виході системи. На підставі (12.38) і (12.54) з урахуванням того, що зображенням Фур’є імпульсної перехідної функції є комплексна передавальна функція, тобто F{w(t)} = W(jw), можна визначити зв’язок між спектральними щільностями вхідного і вихідного випадкових процесів:
Таким чином, спектральна щільність стаціонарного випадкового процесу на виході лінійної системи дорівнює спектральній щільності випадкового процесу на вході системи, помноженій на квадрат модуля комплексної передавальної функції цієї системи. За виразами (12.54) і (12.55) можна розв’язувати не тільки задачу аналізу (визначення характеристик випадкової функції на виході системи), а й задачу синтезу, тобто вибирати параметри динамічної системи таким чином, щоб отримати Rу(t) і Sy(w) близькими до заданих. Розглянемо два важливі випадки проходження випадкового сигналу крізь лінійну систему. Статистичне диференціювання. Під час надходження випадкового сигналу до ідеального диференціювального пристрою з передавальною функцією W(s) = s маємо:
Тоді спектральна щільність вихідної величини (похідної від вхідної величини) буде:
У разі подвійного диференціювання Sх(w) помножується на w4 і т.д. Таким чином, чим більш високі частоти містить спектр випадкового сигналу, тим сильніше вони підсилюються. Це завжди необхідно мати на увазі під час уведення до системи коректувального диференціювального пристрою. У разі значного рівня випадкових завад уведення такої ланки може не привести до поліпшення динамічних властивостей, а навіть погіршити їх. Статистичне інтегрування. Під час надходження випадкового сигналу до ідеального інтегрувального пристрою з передавальною функцією W(s) = 1/s маємо: Тоді спектральна щільність вихідної величини (інтегралу від вхідної величини) буде:
У разі подвійного інтегрування Sх(w) ділиться на w4 і т.д. У даному випадку високі частоти послаблюються (відфільтровуються) інтегрувальною ланкою, на виході якої отримуємо більш згладжений сигнал. Рівняння Вінера-Хопфа Це рівняння встановлює зв’язок між кореляційними функціями вхідного X(t) і вихідного Y(t) сигналів, що діють у лінійній динамічній системі. Відповідно до (12.28) взаємна кореляційна функція цих сигналів має вигляд:
Тоді з урахуванням (12.51) запишемо:
Цей вираз має назву рівняння Вінера-Хопфа. Застосувавши до інтегрального рівняння (12.59) пряме перетворення Фур’є, можна записати: Syx(w) = W(jw)Sx(w) або W(jw) = Syx(w) / Sx(w), (12.60) де Syx(w) і Sx(w) – взаємна і власна спектральні щільності. Застосовуючи до (12.60) обернене перетворення Фур’є, маємо:
Рівняння (12.60) і (12.61) дозволяють знайти динамічні характеристики системи W(jw) і w(t) за відомими імовірнісними характеристиками входу X(t) і виходу Y(t), що визначаються за реалізаціями випадкового процесу.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.165.238 (0.009 с.) |

 , (12.51)
, (12.51) , (12.52)
, (12.52) . (12.53)
. (12.53) . (12.54)
. (12.54) . (12.55)
. (12.55)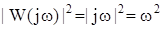 .
. . (12.56)
. (12.56) .
. . (12.57)
. (12.57)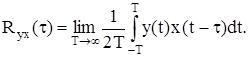 (12.58)
(12.58) (12.59)
(12.59) . (12.61)
. (12.61)


