
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектральні щільності випадкових процесівСодержание книги
Поиск на нашем сайте
Під час дослідження автоматичних систем керування користуються ще однією характеристикою стаціонарного випадкового процесу – спектральною щільністю Sx(w), яка у багатьох випадках є більш зручною, ніж кореляційна функція. Термін “спектральна щільність” походить з теорії електричних коливань. Фізичний зміст спектральної щільності полягає в тому, що вона характеризує розподіл потужності сигналу за частотним спектром (кожна елементарна потужність, яка відповідає нескінченно малій ділянці спектра від w до w + dw, пропорційна значенню функції Sx(w) для даної частоти w). Спектральну щільність можна визначити експериментально через середню величину квадрата амплітуди гармонік реалізації випадкового процесу. Прилади, що застосовують для цього, називаються спектрометрами. Аналітично спектральна щільність Sx(w) випадкового процесу X(t) визначається як перетворення Фур’є кореляційної функції Rx(t):
За допомогою формули Ейлера
Оскільки
Оскільки Sx(w) = Sx(-w). (12.41) Таким чином, спектральна щільність Sx(w) є дійсною і парною функцією частоти w, тому графік цієї функції завжди симетричний відносно осі ординат. Якщо спектральна щільність відома, то за формулою оберненого перетворення Фур’є можна знайти відповідну кореляційну функцію:
З урахуванням (12.25) і (12.42) можна встановити важливий зв’язок між дисперсією Dx і спектральною щільністю Sx(w) випадкового процесу:
Взаємну спектральну щільність Sxg(jw) двох стаціонарних випадкових процесів X(t) і G(t) визначають як перетворення Фур’є від взаємної кореляційної функції Rxg(t):
Взаємна спектральна щільність Sxg(jw) є мірою статистичного зв’язку між двома стаціонарними випадковими процесами X(t) і G(t). Якщо ці процеси некорельовані й мають рівні нулю середні значення, то взаємна спектральна щільність дорівнює нулю, тобто Sxg(jw)=0. На відміну від спектральної щільності Sx(w), взаємна спектральна щільність не є парною функцією w і являє собою не дійсну, а комплексну функцію. Розглянемо без доказу деякі властивості спектральної щільності Sx(w). 1. Спектральна щільність білого шуму є постійною на всьому діапазоні частот (рис. 12.1, г): Sx(w) = N = const. (12.45) Це означає, що енергія білого шуму розподілена за всім спектром рівномірно, а сумарна енергія процесу дорівнює нескінченності, що фізично неможливо. Тобто білий шум є математичною ідеалізацією реального процесу. Походження терміну “білий шум” пояснюється аналогією такого процесу з білим світлом, що має однакові інтенсивності всіх компонент. 2. Спектральна щільність постійного сигналу x(t) = A0 являє собою d-функцію, що розташована на початку координат (рис. 12.1, а): Sx(w) = 2pA02d(w). (12.46) Фізично це означає, що вся потужність постійного сигналу зосереджена на нульовій частоті. 3. Спектральна щільність періодичного сигналу x(t)=Asin(w1t+j) являє собою дві d-функції, що розташовані симетрично відносно початку координат при w = w1 і w = -w1 (рис. 12.1, д):
Це означає, що вся потужність періодичного сигналу зосереджена на двох частотах: w1 і -w1 (для зони додатних частот уся потужність періодичного сигналу зосереджена на одні частоті w1). 4. Спектральна щільність часової функції, що розкладається у ряд Фур’є
Цій спектральній щільності відповідає лінійчатий спектр (рис. 12.2) із d-функціями, що розташовані на додатних і від’ємних частотах гармонік (d-функції умовно зображені так, що їх висоти показані пропорційними коефіцієнтам при одиничній d-функції, тобто величинам
Sx(w)=2Dxa/(a2+w2)= =2DxTx/(1+w2 Tx2), (12.49) де Dx – дисперсія; a = const – параметр затухання; Тх = 1/a - сталий коефіцієнт. Із рис. 12.1, б, в видно, що чим ширше графік спектральної щільності Sx(w), тим вужчий графік відповідної кореляційної функції Rx(t), і навпаки.
Окремі піки на графіку спектральної щільності вказують на те, що випадковий процес змішаний із прихованими періодичними складовими. На рис. 12.3 наведено графік спектральної щільності випадкового процесу, на який накладено один періодичний сигнал з частотою wk. Іноді розглядають нормовану спектральну щільність bх(w), яка має розмірність часу: bх(w) = Sx(w)/Dx. (12.50)
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

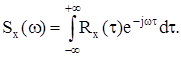 (12.38)
(12.38) вираз (12.38) можна подати у вигляді:
вираз (12.38) можна подати у вигляді: (12.39)
(12.39) - непарна функція t, то другий інтеграл у виразі (12.39) дорівнює нулю. Тоді з урахуванням, що
- непарна функція t, то другий інтеграл у виразі (12.39) дорівнює нулю. Тоді з урахуванням, що  - парна функція t, отримаємо:
- парна функція t, отримаємо: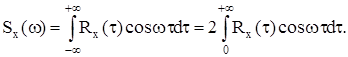 (12.40)
(12.40)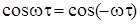 , то з (12.40) випливає:
, то з (12.40) випливає: (12.42)
(12.42) (12.43)
(12.43)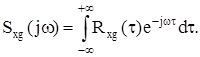 (12.44)
(12.44) . (12.47)
. (12.47) має вигляд:
має вигляд: . (12.48)
. (12.48) .
.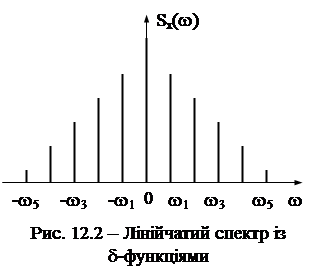 5. Спектральна щільність випадкового процесу, що не містить періодичну складову, являє собою графік без чітко виражених піків (рис. 12.1, б, в). У цьому випадку спектральна щільність апроксимується аналітичним виразом:
5. Спектральна щільність випадкового процесу, що не містить періодичну складову, являє собою графік без чітко виражених піків (рис. 12.1, б, в). У цьому випадку спектральна щільність апроксимується аналітичним виразом: 6. Спектральна щільність випадкового процесу, на який накладені періодичні складові, містить безперервну частину й окремі d-функції, що відповідають частотам цих періодичних складових.
6. Спектральна щільність випадкового процесу, на який накладені періодичні складові, містить безперервну частину й окремі d-функції, що відповідають частотам цих періодичних складових.


