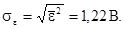Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналітичний метод визначення дисперсії помилкиСодержание книги
Поиск на нашем сайте
Цей метод ґрунтується на припущенні, що спектральні щільності й частотні передавальні функції у виразі (12.66) є дробово-раціональними функціями від w. Тоді (12.66) для спектральної щільності можна подати у вигляді: Si(jw) = |B(jw)|2/|H(jw)|2, (12.72) де B(jw), H(jw) – деякі поліноми від комплексної змінної jw. Обчислення окремих складових дисперсії помилки зводиться до обчислення інтегралів стандартного типу:
де
У додатку Б посібника наведені табличні значення інтегралів Jn для n від 1 до 5 у вигляді формул, що залежать від значень коефіцієнтів a0, a1, …, an і b0, b1, …, bn-1. Таким чином, за аналітичним методом спочатку визначають спектральну щільність помилки Se(w), що складається з доданків вигляду (12.72), і знаходять коефіцієнти ai, bi поліномів H(jw), М(jw). Потім за допомогою стандартних інтегралів Jn визначають окремі складові дисперсії помилки і за (12.68) знаходять саму дисперсію помилки De. Приклад 12.1 На вході замкнутої слідкуючої системи з одиничним зворотним зв’язком (рис. 12.4) діє сигнал U(t), що має спектральну щільність Su(w) = 2DuTu / (1+w2Tu2), а на вході розімкнутої системи діє випадкове збурення F(t) типу “білий шум”, спектральна щільність якого Sf(w) = N. Кореляція між цими сигналами відсутня. Передавальна функція розімкнутої слідкуючої системи: W(s)= k/[s(1+Ts)]. Визначити середню квадратичну помилку системи за таких умов: Du = 100 B; Tu = 20 c; N = 0,01 B2/Гц; Т = 0,1 с; k = 5 c-1. Зазначимо, що у даному випадку зовнішні дії не містять регулярних складових і відповідно до (12.71) середня квадратична помилка співпадає з дисперсією помилки. 1. Знаходимо передавальні функції замкнутої системи за помилкою і за керуванням: Wue(s) = 1/[1+W(s)] = s(Ts+1)/(Ts2+s+k); Wfe(s) = W(s)/[1+W(s)] = k/(Ts2+s+k). 2. Спектральна щільність помилки відповідно до (12.67):
3. За (12.64) знаходимо складову середнього квадрата помилки
Оскільки |jw| = w,
Порівнюючи отриманий вираз із виглядом підінтегральної функції (12.73), можна записати поліноми (для n = 3):
Тобто
Отже, b0 = T2; b1 = -1; b2 = 0. За таблицею Б.1 (додаток Б) знаходимо значення стандартного інтеграла J3:
Тоді отримуємо:
4. Знаходимо складову середнього квадрата помилки
Порівнюючи отриманий вираз із виглядом підінтегральної функції (12.73), можна записати поліноми (для n = 2):
Тобто
За таблицею Б.1 (додаток Б) знаходимо значення стандартного інтеграла J2:
Тоді отримуємо: 5. Знаходимо підсумкове значення середнього квадрата помилки, що дорівнює у даному випадку дисперсії помилки De:
Середнє квадратичне відхилення помилки:
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.83 (0.007 с.) |

 (12.73)
(12.73)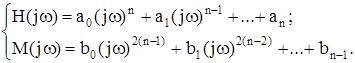 (12.74)
(12.74)
 , що зумовлена керуючим сигналом і співпадає у даному випадку зі складовою дисперсії помилки
, що зумовлена керуючим сигналом і співпадає у даному випадку зі складовою дисперсії помилки  :
: .
. , а
, а  можна подати у вигляді
можна подати у вигляді  , то інтеграл запишемо у вигляді:
, то інтеграл запишемо у вигляді:






 , що обумовлена збуренням, і співпадає у даному випадку зі складовою дисперсії помилки
, що обумовлена збуренням, і співпадає у даному випадку зі складовою дисперсії помилки  :
:


 Отже, b0 = 0; b1 = 1.
Отже, b0 = 0; b1 = 1.