
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез при довільній структурі системи керуванняСодержание книги
Поиск на нашем сайте
Розглянемо систему керування (рис. 12.5). Сумарний сигнал на вході системи дорівнює: U(t) = X(t) + F(t). Вихідний сигнал системи Y(t) зв’язаний з вхідним сигналом U(t) рівнянням: Y(t) = Wз(p)U(t) = Wз(p) [X(t) + F(t)], де Wз(p) – передавальна функція замкнутої системи. Припустимо, що система має відтворювати деяку функцію від керуючого сигналу Z(t) = H(p)X(t), помилка відтворювання дорівнює: E(t) = Z(t) – Y(t). Задача синтезу в разі довільної структури лінійної системи полягає в тому, щоб за відомими статистичними характеристиками корисного сигналу і перешкоди знайти таку оптимальну передавальну функцію замкнутої системи Wз.опт.(р), при можливій фізичній реалізації якої виконувалася б умова (12.78):
Розглянемо спрощену задачу синтезу оптимальної передавальної функції замкнутої системи за таких умов: - задані спектральні щільності корисного сигналу Sx(w) і збурення (завади) Sf(w), а також оператор перетворення Н(р); - корисний сигнал і збурення некорельовані (цей випадок часто зустрічається на практиці); - передавальну функцію спочатку шукаємо без урахування можливості її фізичної реалізації. Для цієї задачі можна записати такий вираз оптимальної передавальної функції (без виведення):
Із (12.80) видно, що єдиними статистичними характеристиками корисного сигналу і збурення, що необхідні для визначення оптимальної комплексної передавальної функції замкнутої системи, є їх спектральні щільності. У загальному випадку ця передавальна функція може виявитися такою, що не реалізується фізично. Зазначимо, що умовою можливості фізичної реалізації системи є рівність: w(t) = 0 при t < 0, тобто реакція системи на d- функцію, що діє на момент часу t = 0, дорівнює нулю при t < 0. Передавальна функція Wз.опт.(s) системи, що фізично реалізується, повинна мати тільки ліві корені. Для того, щоби реалізувати функцію, найбільш близьку до оптимальної, необхідно із Wз.опт.(jw) виділити частину, що фізично реалізується, а решту членів відкинути (наприклад, за методикою Г. Боде і К.Шенона).
Запитання для самоперевірки 1. Яка функція називається випадковою? 2. Що таке реалізація випадкового процесу? 3. Назвіть основні статистичні характеристики випадкового процесу. 4. Що таке одномірна і двомірна функція розподілу? Одномірна і двомірна щільність ймовірності? 5. Що таке білий шум? 6. Які випадкові процеси називаються марковськими? 7. Що таке математичне сподівання? 8. Що таке середнє значення квадрата випадкового процесу? 9. Що таке дисперсія випадкового процесу? 10. Що таке кореляційна функція випадкового процесу? 11. Які випадкові процеси називають ергодичними? 12. Наведіть основні властивості кореляційних функцій. 13. Як пов’язані між собою дисперсія стаціонарного випадкового процесу і кореляційна функція? 14. Що таке спектральна щільність? Поясніть її фізичний зміст. 15. Як пов’язані між дисперсія Dx і спектральна щільність Sx(w) випадкового процесу? 16. Наведіть основні властивості спектральної щільності. 17. Як пов’язані між собою спектральні щільності стаціонарного випадкового процесу на вході й виході лінійної системи? 18. Як пов’язані між собою спектральні щільності стаціонарного випадкового процесу на вході й виході лінійної системи при статистичному диференціюванні? Статистичному інтегруванні? 19. Наведіть рівняння Вінера-Хопфа і поясніть його зміст. 20. Як визначають спектральну щільність помилки Se(w), коли керуючий сигнал і збурення діють одночасно і є корельованими? За відсутності кореляції між процесами U(t) і F(t)? 21. Які існують методи визначення дисперсії помилки? 22. Як визначається дисперсія помилки за аналітичним методом? 23. Що таке задача фільтрації? 24. У чому полягає задача синтезу системи при випадкових впливах? 25. У чому полягає синтез систем керування при заданій структурі? При довільній структурі?
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.202 (0.007 с.) |

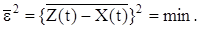
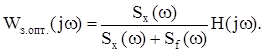 (12.80)
(12.80)


