
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Випадкові та систематичні похибкиСодержание книги
Поиск на нашем сайте Іноді при вимірюваннях виникають значні похибки (промахи), що призводять до явних спотворень результатів вимірювань. Вони виникають внаслідок недогляду експериментатора або неполагодженої апаратури. Такі похибки при вимірюваннях необхідно просто відкидати. Не пов’язані з грубими помилками похибки досліду поділяються на випадкові та систематичні. Багаторазово повторюючи одні і такі самі вимірювання, помічають, що їх результати не точно дорівнюють одне одному, а приймають значення навколо деякого середнього. Похибки, які змінюють величину і знак від досліду до досліду, називають випадковими. Вони можуть бути пов’язані з тертям, люфтами в механічному обладнанні, з недосконалістю об’єкта вимірювання та інші. Систематичні похибки зберігають свою величину і знак під час експерименту. Вони можуть бути пов’язані з помилками приладів (неправильна шкала, нерівні плечі терезів) та з побудовою досліду. Таким чином, внаслідок систематичних похибок, результати досліду коливаються не навколо істинного, а навколо деякого зсуненого значення.
Випадкові похибки.
В якості кращого значення для вимірюваної величини приймають середнє арифметичне зі всіх отриманих n результатів:
тоді істинне значення величини, що вимірюється, може бути записане:
де а х –абсолютна похибка:
З формули (1) бачимо, що
де Характеристикою розсіювання значень x є середньоквадратичне відхилення Середньоквадратичне відхилення Похибку результату не стільки визначають, скільки оцінюють. Оцінка (4) підібрана таким чином, що при проведенні багаточислених серій вимірювань похибка в 2/3 випадків є меншою за У випадку, коли
Довірчим інтервалом називається інтервал Ймовірність
де
Формулу (6) виводять в математичній статистиці з урахуванням того, що: 1. Похибки результатів вимірювань приймають безперервний ряд значень. 2. При великій кількості вимірювань однаково часто зустрічаються похибки одного значення, але різних знаків. 3. Частота появлення похибок зменшується з зростом їх значень. Надійністю результату деякої кількості вимірювань називається ймовірність В спеціальних таблицях коефіцієнтів Ст’юдента
За стандартний інтервал приймають інтервал
тоді результат записують у вигляді:
Такий запис означає, що істинне значення величини, яка вимірюється, знаходиться в інтервалі [
Зворотна до неї величина Систематичні похибки.
Оцінку систематичних похибок експериментатор проводить, аналізуючи особливості методики досліду, паспортну точність приладів. Межею вимірювання приладу називають те значення вимірюваної величини, при якому стрілка приладу відхиляється до кінця шкали. На практиці широко використовуються багатошкальні прилади, тобто прилади, що мають декілька меж вимірювань. Ціна поділки приладу дорівнює значенню вимірюваної величини, яке призводить до відхилення стрілки на одну поділку приладу. Чуттєвістю електровимірювального приладу називають відношення лінійного або кутового переміщення стрілки приладу до вимірювальної величини, що визвала таке переміщення:
де
Наприклад: при силі струму 3 А стрілка амперметра відхилилася на 12 поділок. Чуттєвість даного приладу до струму:
Систематичні похибки електровимірювальних приладів (амперметрів, вольтметрів, мостів, потенціометрів), визначають їх класом точності
де
Наприклад: сила струму 25 мА вимірюється міліамперметром, клас точності якого 0,5, зі шкалою 100 мА. Це означає, що при вимірюванні будь-якого струму в межах 0–100 мА, максимальна абсолютна похибка приладу не перевищує величини:
Так амперметр класу 0,5 дозволяє проводити вимірювання з похибкою, що не перевищує 0,5% від струму, що відповідає повній шкалі приладу. На усіх ділянках шкали – на її початку, в середині і в кінці – ця похибка одна й та ж. В наслідок цього рекомендовано вибирати прилад (або шкалу багатошкального приладу) таким чином, щоб стрілка приладу при вимірюваннях заходила за середину шкали. Електровимірювальні прилади характеризуються класами точності: 0,05; 0,1; 0,2; 0,5; 1,0 та інш. Якщо клас точності приладу не вказаний, то він приймається рівним 4. В реальних дослідах присутні як систематичні так і випадкові похибки. Сумарна похибка знаходиться за формулою:
або
Тоді результат вимірювань записується у вигляді:
З рівняння (5) випливає, що безглуздо домагатися такого результату, при якому В ситуації, коли всі систематичні похибки враховані, клас точності вимірювального приладу відомий і відсутні суттєві невідомі джерела систематичних похибок, можна сформулювати два правила вимірювання: 1. якщо систематична похибка значно перевищує випадкову, вимірювання достатньо проводити один раз. 2. при значних випадкових похибках (у зрівнянні із систематичними) вимірювання слід проводити стільки разів, щоб після статистичної обробки результатів випадкова похибка була меншою за систематичну.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 976; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , (1)
, (1) (2)
(2) (3)
(3) від числа вимірювань залежить слабо, а похибка
від числа вимірювань залежить слабо, а похибка  зі збільшенням кількості вимірювань n зменшується. При n→ ∞
зі збільшенням кількості вимірювань n зменшується. При n→ ∞  , а значить
, а значить  , скільки при значній кількості вимірювань імовірність помилитися на ту ж саму величину у менший чи більший бік є однаковою. Похибка досліду, що розраховується за формулою (3), зі збільшенням кількості вимірювань n зменшується як
, скільки при значній кількості вимірювань імовірність помилитися на ту ж саму величину у менший чи більший бік є однаковою. Похибка досліду, що розраховується за формулою (3), зі збільшенням кількості вимірювань n зменшується як  . Формула (3) може бути записана в іншому вигляді:
. Формула (3) може бути записана в іншому вигляді: (4)
(4)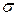 результату спостереження:
результату спостереження: . Чим менша
. Чим менша  , дисперсія
, дисперсія  (5)
(5) , у який попадає істинне значення
, у який попадає істинне значення 
 величини, яка вимірюється, із заданою ймовірністю.
величини, яка вимірюється, із заданою ймовірністю. влучення значення
влучення значення  та дисперсією
та дисперсією  , (6)
, (6) - значення величини, що отримується при вимірюванні.
- значення величини, що отримується при вимірюванні.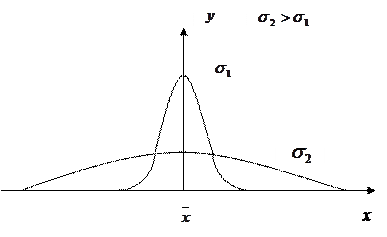
 того, що істинне значення
того, що істинне значення  і вимірюється в частках одиниці або у відсотках.
і вимірюється в частках одиниці або у відсотках. a, N) можна визначити у скільки разів потрібно збільшити довірчий інтервал, щоб при певному числі вимірювань N отримати задану надійність
a, N) можна визначити у скільки разів потрібно збільшити довірчий інтервал, щоб при певному числі вимірювань N отримати задану надійність  :
: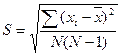 , (7)
, (7) (8)
(8) ] з надійністю
] з надійністю 
 . Мірою точності результатів вимірювань є відносна похибка, що виражається у відсотках:
. Мірою точності результатів вимірювань є відносна похибка, що виражається у відсотках: ×100%.
×100%. називається точністю.
називається точністю. ,
, - лінійне або кутове переміщення;
- лінійне або кутове переміщення;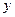 - значення величини, що вимірюється.
- значення величини, що вимірюється. .
. , який виражають в відсотках:
, який виражають в відсотках: ,
, - максимальна абсолютна похибка приладу;
- максимальна абсолютна похибка приладу; - значення вимірюваної величини, що відповідає переміщенню стрілки на всю шкалу приладу.
- значення вимірюваної величини, що відповідає переміщенню стрілки на всю шкалу приладу.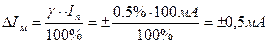 .
. ,
, . (9)
. (9)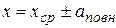 . (10)
. (10) <<
<<  . Навпаки, необхідне число вимірювань n можна визначити за умови
. Навпаки, необхідне число вимірювань n можна визначити за умови 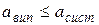 і майже завжди достатньо вибрати
і майже завжди достатньо вибрати  .
.


