
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ефект Холла у напівпровідниках.Содержание книги
Поиск на нашем сайте
ПРИЛАДИ: універсальне джерело живлення; цифровий вольтметр; соленоїд; датчик Холла. 1. Енергетичні зони. Провідність більшої кількості твердих тіл пов’язана з рухом електронів. Електрони входять у склад атомів всіх тіл, але деякі з тіл не проводять електричний струм (діелектрики), а інші є добрими його провідниками. Причина відмінності полягає в особливостях енергетичного стану електронів на зовнішніх електронних оболонках атомів у цих речовинах. При з’єднанні N атомів у тверде тіло (у кристал) характер руху зовнішніх електронів суттєво змінюється. Ці електрони втрачають зв’язок зі “своїм” атомом та належать кристалу в цілому. Кожному рівню енергії електронів ізольованого атому відповідає у кристалі група N близьких по енергії рівнів, що об’єднуються в зону. Ця кількість в реальних кристалах, де атомів» 1022 см-3, дуже велика, а ширина зони не перевищує декілька електронвольт. Таким чином різниця в енергії між найближчими рівнями надто мала. Деякі рівні енергії електронів зливаються так, що відрізнити окремі рівні неможливо. Але кількість рівнів, які з’єдналися у зону, при злитті не змінюється. Вона визначає найбільшу кількість електронів, яка може “знаходитися у зоні (згідно з принципом Паулі, кожний електрон займає свій власний енергетичний рівень. Враховуючи, що спін електрона може бути - Допустимі зони діляться забороненими зонами - областями, в яках нема дозволених енергетичних рівнів (рис.11.1). Це означає, що узагальнені електрони у кристалі можуть мати не будь-яку енергію, а лише енергію, яка відповідає одній із допустимих зон. Перейти з зони в зону “нагору” електрон може лише поглинувши квант енергії, рівний ширині забороненої зони. Навпаки перехід “вниз” можливий лише після випромінення кванту енергії. Переходи типу “зона” – “зона” найчастіше не означають, що електрон переміщується в просторі кристалу. Має місце збудження електрону, коли він поглинаючи квант енергії переходить “нагору”, або релаксація, коли він випромінює квант енергії і переходить “вниз”. Зазначені переходи можливі лише тоді, коли “вгорі” або “внизу” є вільні, не заповнені електронами енергетичні рівні. Коли всі рівні зайняті переходи заборонені принципом Паулі. Найвища по значенню енергій електронних рівнів з дозволених зон, рівні якої вільні від електронів називається «вільною зоною», або «зоною провідності». Найвища із заповнених зон називається «валентною зоною». Над нею за забороненою зоною знаходиться зона провідності. При збудженні атому (поглинанні енергії) один із валентних електронів може набути енергії, що перевищує ширину забороненої зони, і «перейти» в зону провідності. Просторово це означає, що електрон із зв’язаного стану (знаходився на валентній оболонці в атомі) переходить у вільний стан і набуває здатності вільно рухатись по кристалу. Цей рух не є орбітальним, як у атомі, а поступальним. При цьому напрямок руху хаотично змінюється. Звісно, що у кристалі кожному рівню, який відповідає руху електрона у один бік, відповідає рівень, який має ту ж саму енергію та який відповідає руху електрона з тим же імпульсом у протилежному напрямку.
Рис.11.1. Формування енергетичних рівнів.
Таким чином, у відсутності зовнішніх електричних полів електричний струм рівний нулю. Положення змінюється у присутності поля. Під дією електричного поля стан руху в один бік - по полю - стає енергетично більш вигідним, ніж рух в інший бік. Необхідно розрізняти три випадки. Діелектрики. Якщо валентна зона до кінця заповнена електронами, а зона провідності зовсім пуста, то зовнішнє електричне поле не може змінити рух електронів. В вільній зоні електрони не рухаються, оскільки електронів з такими енергіями не має. В повністю заповненій зоні рух відсутній, бо рух супроводжується зміною енергії, тобто переходом електрону на інший енергетичний рівень. Однак вільних рівнів немає. Речовина з таким заповненням зон називається діелектриком. Провідники. Положення змінюється, якщо у кристалі є зона, частково заповнена електронами, зона провідності. У цьому випадку зовнішнє електричне поле може змінити розподіл електронів по рівням енергії та створити упорядкований рух електричних зарядів. Частково заповнена зона є у всіх твердих провідниках електричного струму; також вона є у всіх металах. Напівпровідники відрізняються від діелектриків тим, що в них ширина забороненої зони, розташованої над валентною, не на багато більша теплової енергії. Тепловий рух перекидає частину електронів з валентної зони у вільну - зону провідності. При цьому у вільній зоні з’являються електрони, а в заповненій зоні - вільні місця, “дірки”. У цьому випадку електрони обох зон приймають участь у переносі заряду. Кількість носіїв струму у напівпровідниках значно залежить від температури, експоненціально збільшуючись з її підвищенням. При низьких температурах - поблизу абсолютного нуля - напівпровідники мають властивості діелектриків.
2. Електронна та діркова провідність. При дослідженні електричних властивостей речовини важливо розрізняти випадки, коли зона провідності зайнята незначно або, навпаки, майже до кінця. В мало заповненій зоні електрони займають нижні енергетичні рівні, які розташовані біля її дна. Рух цих електронів мало відрізняється від руху вільних електронів. У цьому випадку говорять, що провідність належить до електронного типу. Існує інший тип провідності, що носить назву “дірковий”. В цьому випадку процеси переносу заряду відбуваються наступним чином. Валентна зона повинна бути не повністю заповненою, тобто в ній існують вільні рівні. Припустимо, що біля якогось із атомів з’явилося вільне електронне місце в ковалентному зв’язку – вакансія, що має позитивний заряд. В результаті флуктуацій якийсь із безлічі електронів, що рухається навколо сусідніх атомів, може покинути своє місце і зайняти вакансію. Такий електрон може виконати поступальний рух. Але він сам звільнив позитивну вакансію. Остання через певний час, який необхідний для створення необхідних умов для “стрибка” іншому електрону, теж буде заповнена, але звільниться інша. Рух електронів має “стрибкоподібний характер”. Якщо таких вільних рівнів дуже багато, то електрон, відірвавшись від свого атому в силу випадкового збігу обставин, наприклад, поглинувши квант теплової енергії, починає перескакувати з рівня на рівень і рухатись по кристалу практично ніде не затримуючись. Рух електрону в цьому випадку нагадує вільний, але має “стрибкоподібний” характер. Математично зазначений стрибкоподібний характер руху електрону описувати важко. Зручніше ввести до розгляду уявний, “віртуальний” носій позитивного заряду – вакансію або “дірку”. Рух вакансій направлений протилежно руху електронів, його зручніше описувати тим же математичним апаратом, що й рух вільних електронів, оскільки рух вакансій можна вважати вільним. Для дірки, як і для електрону, вводять поняття ефективної маси, при цьому Електронний тип провідності характерний для більшості чистих металів. Але в ряді металів (берилій, кадмій та деякі інші) основними носіями електричного струму є дірки. Питома електрична провідність провідника залежить від концентрації n та рухомості b носіїв струму. Рухомістю b (іноді m)називають відношення середньої упорядкованої швидкості
Густина струму у провіднику рівна
де s - питома електрична провідність. З іншого боку
де е - заряд електрона. Порівнюючи (11.1) та (11.1а) побачимо, що питома електрична провідність визначається, як
3. Власна та домішкова провідність. Хімічно чисті напівпровідники мають провідність, яка пов’язана з невеликою кількістю електронів у зоні провідності та тією ж кількістю дірок у валентній зоні. Така провідність називається власною - вона не пов’язана з домішками. Невелике додавання домішок до напівпровідника, яке називається легуванням, може значно змінити його електричні властивості. Одні домішки різко збільшують концентрацію електронів у зоні провідності у порівнянні із концентрацією дірок у валентній зоні. Інші, навпаки, збільшують кількість дірок у валентній зоні. При цьому зразок, звісно, зберігає свою електронейтральність (сумарний заряд зразка рівний нулю). Перші з напівпровідників називаються електронними (або напівпровідниками n – типу), а інші - діркові (або напівпровідниками р –типу). У загальному випадку у процесі електричної провідності приймають участь як електрони, так і дірки. Питома електрична провідність напівпровідника у цьому випадку рівна
s = е (nbn + pbp), (11.3)
де n та р - концентрація електронів та дірок, b n та b p - їхні рухомості. У випадку домішкової провідності один тип носіїв як завжди переважає над іншим, та у рівнянні (11.3) можна знехтувати однією з складових.
4. Визначення концентрації носіїв заряду п та їх рухомості b. Рівняння (11.2) показує, що дослідження електричної провідності провідників дозволяє визначити добуток nb. Як побачимо нижче, дослідження ефекту Холла дозволяє знаходити концентрацію носіїв n, після чого можна знайти їх рухомість b. Таким чином, одночасне дослідження електричної провідності та ефекту Холла дозволяє експериментально знаходити найважливіші параметри, які визначають стан електронів у металах та напівпровідниках.
5.Ефект Холла. Нехай через однорідну пластину вздовж вісі Y тече струм І (рис. 11.2). Якщо цю пластину помістити у магнітне поле, напрямлене по осі Z, то між передньою та тильною гранями А та Б з’являється різниця потенціалів. Насправді, на електрон який рухається зі швидкістю
де е - заряд електрона,
Рис.11.2.Схема, яка пояснює ефект Холла.
У нашому випадку ця сила напрямлена по осі Х:
F х = e υy Bz, (11.5)
Під υy ми розуміємо середню - дрейфову - швидкість електронів, яка виникає при накладенні на зразок зовнішнього електричного поля. Під дією сили Лоренца F л електрони відхиляються до грані А, заряджаючи її негативно. На грані Б накопичується нескомпенсовані позитивні заряди. Це призводить до виникнення електричного поля Ех, направленого від Б до А, та до появи різниці потенціалів ∆UАБ між гранями А та Б, яку можливо виміряти
∆UАБ = Ехl. (11.6)
Поле Е х діє на електрон із силою Fх = e Eх, що напрямлена проти сили Лоренца. У встановленому стані сила Fх зрівноважує силу Лоренца F л, тому подальше накопичення зарядів на бокових гранях пластини припиняється. З умови рівноваги F л = Fх, тобто е υy Bz = e E x знайдемо: Ex= υy Bz. (11.7)
Враховуючи, що сила струму І рівна І = ne υy l a (11.8)
та підставляючи (11.7) та (11.8) у (11.6) знайдемо:
∆UAБ = IBz / nea = RХол.IBz / a. (11.9)
Стала RХол. називається сталою Холла. Як бачимо з (11.9),
У напівпровідниках, коли внесок у провідність обумовлений електронами та дірками, вираз для сталої Холла має більш складний вигляд:
де n, p - концентрація електронів та дірок; b n, b p - їх рухомість. Якщо головний внесок до ефекту вносить один з носіїв, то для сталої Холла можна користуватися рівнянням (11.10). Коли вимірюємо величину R x, можна за допомогою (11.10) знайти концентрацію носіїв струму n, а по знаку різниці потенціалів, яка з’являється між гранями А та Б, встановити характер провідності - електронний або дірковий.
Експериментальна установка.
Рис.11.3. Схема експериментальної установки для дослідження ефекту Холла.
Датчик Холла розміщується у середині соленоїда на вимірювальному стержні, котрий може переміщуватися вздовж осі. Крізь датчик пропускаємо струм від універсального джерела живлення. Під дією магнітного поля соленоїда в датчику виникає Е.Р.С. Холла, котра вимірюється цифровим вольтметром. Схема експериментальної установки зображена на рис. 11.3.
Завдання.
1. Увімкнути універсальне джерело живлення та цифровий вольтметр. 2. Зняти залежність Е.Р.С. Холла від відстані до центру соленоїда вздовж його осі ∆Vексп = (х). Побудувати графік, відклавши по осі ординат ∆Vексп (х) / ∆Vексп(0). 3. На тому ж графіку побудувати теоретичну криву залежності магнітного поля соленоїда від відстані
нормовану на значення індукції при X = 0 (B теор(x) / B теор(0)), де L - довжина соленоїда; х - відстань від центру соленоїда до точки дослідження; R - радіус соленоїда; m - кількість витків на одиницю довжини соленоїда;
4. Скориставшись теоретичним значенням індукції магнітного поля в центрі соленоїда В теор(0), визначити за формулою (11.9) значення сталої Холла та за формулою (11.10) концентрацію носіїв n. Для цього використати виміряне значення Е.Р.С. Холла в цій точці. Сила струму І через датчик Хола рівна 90 мА (рис. 11.3). Даний пункт виконати не менш трьох раз для різних значень струму, що протікає через соленоїд.
Дані для розрахунку.
а = 0,2 мм N = mL = 2500 l = 1,5 мм L = 168мм в = 1 мм R = 30 мм
Контрольні запитання.
1.Які речовини називаються діелектриками, провідниками, напівпровідниками? Чим пояснити різницю їх електричних властивостей? 2. Що називається стала Холла? У яких речовин - у провідників чи напівпровідників - стала Холла більш залежить від температури, чому? 3. Вираз для сталої Холла був отриманий без врахування розподілу електронів за швидкостями. На скільки це справедливо у випадку металів та напівпровідників?b 4. Чи залежить результат вимірювання сталої Холла від геометрії зразків? 5. Дати визначення рухомості носіїв заряду, у яких одиницях вона вимірюється? 6. Записати вираз для питомої електричної провідності провідника, напівпровідника? Вказати розмірність величини s. 7. Чому рівна Е.Р.С. Холла? Як визначити характер провідності об’єкта дослідження за допомогою ефекту Холла? 8. Показати напрямки відхилення носіїв заряду в напівпровідникому зразку, що містить і електрони, і дірки в рівній кількості. Чому дорівнює в цьому випадку Е.Р.С. Холла?
Дані вимірювання занести в таблицю:
Література.
1. Сивухин Д.В. Общий курс физики. - М.: Наука, 1983, п. 98. 2. Парсел Е. Электричество и магнетизм. - М.: Наука, 1983, гл. 4, п. 4 - 6; гл. 6, п. 9. 3. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. - М.: Наука, 1983.
Лабораторна робота № 12
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.43.98 (0.008 с.) |

 або +
або + 
 . Маса дірки більша за масу вільного електрона, оскільки дірка більш інерційна, ніж вільний електрон. Останнє викликано, як було зазначено раніше, тим, що рух дірки викликаний перескоком електрону з зайнятого ним рівня на вакансію. А для цього потрібен більший час, ніж вільному електрону для подолання такої ж відстані.У цьому випадку говорять про дірковий тип провідності.
. Маса дірки більша за масу вільного електрона, оскільки дірка більш інерційна, ніж вільний електрон. Останнє викликано, як було зазначено раніше, тим, що рух дірки викликаний перескоком електрону з зайнятого ним рівня на вакансію. А для цього потрібен більший час, ніж вільному електрону для подолання такої ж відстані.У цьому випадку говорять про дірковий тип провідності. носіїв (електронів та дірок) до напруженості зовнішнього електричного поля Е, яке спричиняє цей рух
носіїв (електронів та дірок) до напруженості зовнішнього електричного поля Е, яке спричиняє цей рух .
. , (11.1)
, (11.1) , (11.1а)
, (11.1а)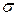 = n e b. (11.2)
= n e b. (11.2) в поперечному магнітному полі, діє сила Лоренца:
в поперечному магнітному полі, діє сила Лоренца: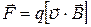 (11.4)
(11.4)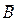 - індукція магнітного поля.
- індукція магнітного поля.
 . (11.10)
. (11.10) ,
,
 ,
, - загальна кількість витків соленоїда.
- загальна кількість витків соленоїда.


