
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики електровимірювальних приладів.Содержание книги
Поиск на нашем сайте
Границею вимірювання приладів вважають те значення вимірювальної величини, при якому стрілка приладу відхиляється до кінця шкали. На практиці широко використовуються прилади, які мають багато шкал тобто прилади, що мають декілька границь вимірів. Ціна поділки приладу дорівнює значенню вимірюваної величини, яке викликає відхилення стрілки на одну поділку шкали приладу. Нехай, наприклад, вольтметр має дві границі вимірювання: 10 та 30 В. Шкала має 100 поділок. Ціна поділки для границі 10 В дорівнює 0,1 В/поділ., для границі 30 В вона дорівнює 0,3 В/поділ. Чутливістю електровимірювального приладу називають відношення лінійного або кутового переміщення стрілки приладу (у поділках шкали) до вимірюваної величини, що викликало це переміщення: d= D/y, (1.6) де D- лінійне або кутове переміщення; y - вимірювана величина.
Нехай, наприклад, коли струм дорівнює 3А стрілка амперметра відхилилася на 36 поділок. Чутливість даного приладу до струму дорівнює
Електровимірювальні прилади характеризуються класом точності: 0,05; 0,1; 0,2; 0,5; 1,0 та ін. Якщо клас точності на приладі не вказаний, то він вважається рівним 4. Число, яке відповідає класу точності приладу, визначається у відсотках як відношення максимальної абсолютної похибки приладу до значення вимірюваної величини, яке відповідає переміщенню стрілки на всю шкалу приладу:
де g - клас точності приладу, що позначений на шкалі приладу; yп - значення вимірюваної величини, відповідне переміщенню стрілки на всю шкалу приладу; Dym - максимальна абсолютна похибка приладу.
Як видно, Dyт легко визначається з формули (1.7) при наявності інформації стосовно класу точності приладу. Слід відрізняти клас точності приладу від його відносної похибки, яка обчислюється за формулою:
де
Пояснимо сказане на прикладі. Нехай струм силою 25 мА виміряний міліамперметром класу точності 0,5 зі шкалою на 100 мА. Це означає, що при вимірюванні будь-якого струму в межах 0 - 100 мА максимальна абсолютна похибка не перевищує величини
Отже, відносна похибка даного вимірювання становитиме:
З наведеного прикладу бачимо, що при вимірюванні на початку шкали приладу відносна похибка результату різко зростає. Тому, якщо необхідно провести вимірювання з високою точністю, слід підібрати такий прилад, щоб вимірювана фізична величина викликала відхилення стрілки більш ніж на половину шкали.
В останній час широке застосування знаходять цифрові електровимірювальні прилади. Ці прилади не мають рухомих частин. Їх дія заснована на використанні підсилювачів та цифрових індикаторів. Усе сказане вище за клас точності та ціну поділки повністю відноситься і до цих приладів.
Метод Уітстона.
Класичним методом вимірювання опору є метод містка постійного струму. На рис. 1.2 зображена схема найпростішого містка, що має назву міст Уітстона. Вона складена із чотирьох послідовно з’єднаних опорів, що утворюють чотирикутник АВCDA. В одну із діагональних гілок DB вмикається чутливий гальванометр Г, а в другу - джерело е.р.с. Е.
Рис. 1.2 Принципова схема моста Уітстона.
Вимірюваний опір r x утворює гілку AB, у гілку BC вмикається магазин опору r 0. Ділянка ADC (опори r 1 та r 2) утворюється реохордом. По реохорду переміщується рухомий контакт D (повзунок), який дозволяє вимірювати відношення між опорами r 1 та r 2. Струм який проходить через гальванометр, залежить від опорів r x, r 0, r 1 та r 2. Переміщуючи контакт реохорду, можна знайти таке його положення, при якому струм, який проходить через гальванометр, дорівнює нулю. У цьому випадку говорять, що місток збалансовано. При балансі потенціали точки В і D рівні: Визначимо умови, за яких потенціали точок B і D рівні. Для цього необхідно, щоб, по-перше, падіння напруги на ділянках АВ та AD було однаковим по відношенню до точки А. По-друге, падіння напруги на ділянках ВС та DC було однаковим по відношенню до точки С. Знайдемо аналітичні вирази умов, виконання яких забезпечує баланс моста. Позначаючи струм в гілці ABC через i 1, а у гілці ADC через i 2, отримуємо: i1rx = i2r1 i1r0 = i2r2, (1.9) звідси rx=r0 r1/r2 . (1.10)
Опір реохорду з однорідного провідника пропорційний його довжині, оскільки
Визначення опору зводиться, таким чином, до визначення довжин ділянок реохорду. Взагалі виміряти величину опору r х можливо при будь-якому r 0. В залежності від величини r 0, балансировка містка відбувається при різних значеннях відношення l1/ (L - l1). Визначимо, як залежить точність вимірювання r х від положення контакту D при балансі містка. При цьому для визначеності будемо вважати, що похибка у вимірюванні положення повзунка (точніше кажучи довжини l 1 ) є єдиним джерелом похибок дослідження. Якщо продиференціювати (1.11) знайдемо абсолютну похибку, з якою визначається величина опору r х:
З (1.11) та (1.12) знайдемо відносну похибку:
Похибка вимірювань залежить, таким чином, від величини l1/L. Позначимо дріб [(1 - l1/L)l1/L] -1 через х, тоді
Залежність х від l1/L зображена на рис. 1.3.
Рис. 1.3 Графік залежності відносної похибки вимірюваного опору від положення контакту на реохорді.
Як видно із графіка, найбільш точними є вимірювання, зроблені при l 1 /L = 0,5. При l 1 /L = 0,2 або 0,8 похибка вимірювань зростає в 1,5 рази, а при подальшому наближенні l1/L до нуля або одиниці приводить до все більш скорішого зростання похибки. Тому опір магазину r0 треба завжди вибирати так, щоб баланс містка досягав при положенні контакту приблизно по середині реохорда і у будь-якому випадку у межах 0,2 < l1/L < 0,8. Використана у роботі схема містка Уітстона зображена на рис. 1.4 має деякі відмінності від розглянутої вище принципової схеми містка (Рис. 1.2). Особливості роботи схеми, приведеної на рис. 1.4, наступні: 1. Джерело е.р.с. Евмикається в коло за допомогою перекидного перемикача К, що дає змогу виконувати вимірювання при різних напрямках струму у вітках містка. Результат досліду не повинен, зрозуміло, залежати від зміни полярності підключення батареї. Така залежність може виникати у тому випадку, якщо у схемі є паразитні термо-е.р.с. або контакти, що мають властивості детектора (по-різному проводять струм у різних напрямках). Якщо результат досліду залежить від зміни полярності підключення батареї, необхідно перевірити надійність контактів схеми та усунути причину цієї залежності. 2. Підключення містка до джерела живлення здійснюється через дільник напруги, який захищає гальванометр від протікання великих струмів при незбалансованому містку. По мірі того, як місток наближається до балансу, покази гальванометра зменшуються, напругу на реостаті можна збільшувати, що підвищує чутливість вимірів. 3. Всі вимірювання необхідно робити при короткочасному натисканні на ключ К тому, що тривале протікання струму у схемі веде до нагріву опорів та до зміни їх величин.
Порядок виконання роботи.
1. Скласти робочу схему містка Уітстона, зображену на рис. 1.4.
Рис. 1.4 Робоча схема містка Уітстона.
2. Встановити повзунок D на середині реохорда. 3. Підібрати таке значення опору r 0, при якому покази гальванометра наближаються до нульових значень. Підвищити чутливість вимірів переміщенням рухомого контакту реостату R, тобто збільшити напругу, що подається в діагональ АС. Тоді згідно (1.11)
4. Повторити балансування містка шляхом зміни положення повзунка реохорду. Зафіксувати в протоколі вимірювань значення r 0 та довжину ділянки реохорду l.
5. Змінити за допомогою ключа К напрям струму у колі на зворотній та знов провести виміри ділянки реохорду l 1. 6. Знайти середнє значення l 1 для кожного з положень ключа, а потім усереднити результати вимірів. 7. Вказаним способом здійснити відповідні вимірювання для двох опорів rx 1 та rx 2 окремо. Після цього, з’єднати їх послідовно, потім паралельно і виконати вимірювання, передбачені п.п. 2÷5. 8. За знайденими величинами невідомих опорів rx 1 та rx 2 обчислити значення опорів при їх послідовному та паралельному з’єднаннях (r посл., r парал.). Порівняти результати розрахунку з даними, отриманими з досліду. 9. Оцінити похибки вимірів.
Дані вимірювання занести у таблиці:
Контрольні запитання 1. Що називають межею вимірювання приладу? 2. Як визначити ціну поділок вимірювального приладу? 3. Що таке клас точності приладу? Як визначити максимальну абсолютну похибку приладу? 4. Що називають чутливістю вимірювального приладу? 5. Зобразити принципову схему містка Уітстона. Пояснити, яким чином можливо виміряти опір за допомогою містка Уітстона. 6. Як залежить відносна похибка вимірювання невідомого опору від положення повзунка на реохорді містка Уітстона? 7. Що таке збалансований місток Уітстона? 8. Записати аналітичні вирази умов, за виконання яких забезпечує баланс містка Уітстона. Література 1. Сивухин Д.В. Общий курс физики. Т.3. Электричество. - М.: Наука, 1977. 2. Лабораторные занятия по физике. Під ред. Гольдина Л.Л. - М.: Наука, 1983.
Лабораторна робота № 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.20.178 (0.012 с.) |


 .
. , (1.7)
, (1.7)
 × 100%, (1.8)
× 100%, (1.8) - поточне значення вимірюваної величини.
- поточне значення вимірюваної величини. .
. .
.

 , тобто різниця потенціалів між цими точками дорівнює нулю
, тобто різниця потенціалів між цими точками дорівнює нулю  =
=  = 0. Останнє приводить до того, що струм в точці В не розгалужується і в діагоналі BD не протікає. Відповідно стрілка гальванометра Г не відхиляється.
= 0. Останнє приводить до того, що струм в точці В не розгалужується і в діагоналі BD не протікає. Відповідно стрілка гальванометра Г не відхиляється. . Позначаючи довжину ділянки r 1 через l 1, довжину r 2 через l 2 та повну довжину реохорда через L, знайдемо:
. Позначаючи довжину ділянки r 1 через l 1, довжину r 2 через l 2 та повну довжину реохорда через L, знайдемо: . (1.11)
. (1.11) . (1.12)
. (1.12) (1.13)
(1.13)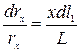 .
.

 .
.


