
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Експерементальна перевірка закона Кюрі - вейсаСодержание книги
Поиск на нашем сайте
ПРИЛАДИ: зразок феромагнетика; трансформатор, первинна обмотка якого виконує роль нагрівної спіралі, а вторинна – вимірювальна, цифровий вольтметр; термопара; гальванометр.
Магнітні властивості тіл, в основному, обумовлені поведінкою електронів, які входять до складу атомів та молекул. Електрони рухаються по атомним та молекулярним орбітам. Цей рух еквівалентний проходженню деякого кругового (молекулярного) струму, який, в свою чергу, сприяє виникненню магнітного поля. Крім цього електрони володіють власним механічним моментом - спіном. Обертання електрона навколо власної осі також збуджує у просторі магнітне поле.
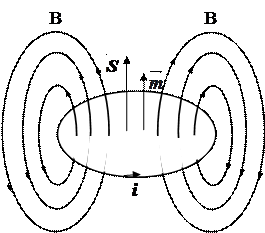
Рис. 13.1 Силові лінії магнітного поля кругового струму.
Розглянемо молекулярний струм і, який обтікає круглий контур площею S (рис.13.1). В електродинаміці доведено, що напруженість магнітного поля, яка викликана струмом, на віддаленні від нього залежить тільки від добутку величини струму у контурі на його площу S (залежність від відстані між контуром та точкою спостереження нас зараз цікавити не буде). Величина m= іS називається магнітним моментом струму. Магнітний момент т та відстань від контуру до точки спостереження повністю визначає магнітне поле: знати величину струму і та площу S окремо немає потреби. Магнітний момент є вектором. Він розташований на нормалі до площини контуру,а його напрямок співпадає з напрямком магнітного поля у центрі витка. Введемо вектор площадки
Розмістимо контур зі струмом у магнітному полі. Енергія, яку придбає при цьому контур, залежить від величини
w = -
Енергія контуру у полі мінімальна, якщо напрямок Магнітний стан речовини характеризується вектором намагніченості
де V (об'єм, в якому знаходиться магнітний момент). В діа- та парамагнетиках вектор намагніченості
Коефіцієнт пропорційності c має назву магнітної сприйнятливості речовини. Якщо c має негативне значення, то речовина називається діамагнетиком, а якщо позитивне - парамагнетиком. Теорія показує, що речовини, у котрих у кожному атомі (чи молекулі) електронні струми та спіни направлені у різних напрямках, так, що їх магнітні моменти компенсують один одного, являються діамагнетиками. В цих речовинах сумарний (атомний) магнітний момент дорівнює нулю. Речовини з відмінними від нуля атомними магнітними моментами володіють парамагнетизмом. Зовнішнє поле у першому випадку створює магнітний момент атомів (цей момент з'являється із-за прецесії електронів у магнітному полі), а у другому - орієнтує наявні магнітні моменти, які до цього розташовувались у просторі хаотичним чином. Прикладом прецесії є складний рух дзиґи, що обертається навколо власної осі і, крім того, вісь обертання додатково рухається навколо вертикалі (напрямку гравітаційного поля).
Рис. Прецесія дзиґи.
Прецесувати дзиґа починає тоді, коли швидкість обертання зменшується (вплив тертя). Як наслідок – зменшується механічний момент обертання і гравітаційне поле звалює дзиґу. Проте залишковий механічний момент “намагається” утримувати її вертикально. Наслідком даної конкуренції і є виникнення прецесії дзиґи. У випадку діамагнетика орбітальний магнітний момент електрона утримує вісь обертання електрона в тому напрямку, який був до ввімкнення магнітного поля. Саме ж поле намагається переорієнтувати магнітний момент електрона, що також приводить до додаткового прецесійного руху електрону. Як відомо, будь який рух електрона викликає появу відповідного магнітного поля. В даному випадку виникає додаткове прецесійне магнітне поле електрону і відповідний прецесійний магнітний момент. Прецесійне магнітне поле спрямоване проти збуджуючого поля, тому діамагнетики намагнічуються протилежно збуджуючому полю і послаблюють його. Парамагнітні властивості розглянемо на прикладі атому, в якому магнітний момент пов'язаний з напрямом спіна одного - єдиного електрона. Як відомо, проекція власного механічного моменту електрона (спіна) на будь-який напрямок, який виділено (в нашому випадку на напрямок магнітного поля) може дорівнювати чи +
w = ± mB ½
Згідно співвідношенню Больцмана, кількість атомів, магнітний момент яких напрямлений по полю та проти поля, дорівнює відповідно
N± = N0exp (- w kT) = N0exp (±mB B /kT), (13.5)
де N0 - нормована константа, яка залежить від густини електронного газу у речовині. При не дуже низькій температурі експоненту можна розкласти в ряд:
N± = N0 (1± mB B / kT). (13.6)
Магнітний момент речовини пропорційний, при цьому, різниці кількості атомів з позитивними та негативними напрямками магнітного моменту, тобто
Порівнюючи формулу (13.7) з вищенаведеним виразом c ~ 1 / T. (13.8)
Цей висновок діє у тих випадках, коли магнітний момент атома відрізняються від магнетона Бора і може мати більш ніж дві проекції на напрямок поля. Звернемося тепер до феромагнетиків. У них існують сили, які призводять до того, що механічні, а разом з ними і магнітні моменти сусідніх атомів орієнтуються паралельно один до одного. Ці сили мають квантомеханічну природу і не мають класичного аналогу. Вони носять назву “обмінних сил”. Речовини, у яких магнітні моменти суміжних атомів орієнтуються у протилежних напрямках, мають назву антиферомагнетиків. Обмінні сили у феромагнетиках призводять до того, що у будь-якій невеликій області вектор намагніченості Кореляція напрямків магнітних моментів сусідніх атомів, що належать одному домену, пов’язана, як зазначено вище, з обмінними силами. Теплове коливання атомів цю кореляцію руйнує. Тому феромагнітні речовини при високих температурах втрачають свої феромагнітні властивості і перетворюються у звичайні парамагнетики. Перехід від феро - у парамагнітний стан є типовим прикладом фазового переходу. Він відбувається стрибком при досить визначеній для кожної речовини температури, яка носить назву температури Кюрі - Т с. Для парамагнітних речовин, які при зниженні температури стають феромагнітними, формула (13.8) повинна бути видозмінена. Ця формула показує, що температура Т = 0 являється особливою точкою температурної кривої, в якій c безмежно зростає. При Т→ 0 тепловий рух атомів відсутній, тому ніщо не заважає магнітним моментам атомів орієнтуватися в одному напрямку при скільки завгодно слабкому зовнішньому полі. В нагрітих феромагнетиках це трапляється під впливом обмінних сил при пониженні температури не до абсолютного нуля, а до температури Кюрі. Таким чином у феромагнетиків закон Кюрі повинен бути замінений законом Кюрі - Вейса:
де С – константа, що залежить від роду речовини, Т с - температура Кюрі. Ця формула справедлива при Т > Тс. Міркування, які привели до формули (13.9), не є строгими. Формула (13.9) добре описує поведінку феромагнітних речовин при переході в парамагнітну фазу при помітному перевищенні температури над точкою Кюрі Тс, але втрачає точність при Т» Тс. Іноді для уточнення формули (13.9) вводять замість однієї дві температури Кюрі, одна з яких описує точку фазового переходу - феромагнітна точка Кюрі Тө, а інша є параметром у формулі (13.9) - парамагнітна точка Кюрі Тс (рис. 13.2). Метою цієї роботи є вивчення температурної залежності c ( Т ) феромагнетика при температурах вище точки Кюрі.
Рис.13.2. Залежність зворотної величини магнітної сприйнятливості феромагнетика від температури.
Схема експериментальної установки приведена на рис. 13.3. В невелику електричну піч вставлять феромагнетик F. Розігріваюча обмотка печі являє собою циліндричний соленоїд, магнітне поле якого помітно збільшується феромагнітним осердям. Магнітний потік Ф, створений електричним струмом в первинній (нагрівній) обмотці, підсилений наявним феромагнітним сердечником, буде змінюватись у часі Величина Е.Р.С. визначається як:
де знак мінус показує, що Е.Р.С. індукції завжди намагається рухати електрони в напрямку, який би перешкоджав зміні магнітного потоку. Таким чином, змінна напруга U нагр.(t) створює в первинній обмотці струм i(t), що в свою чергу обумовлює виникнення змінного магнітного потоку Ф (t). Цей потік індукує у вторинній обмотці напругу U вим., яку можна виміряти вольтметром. Отже, нагрівна піч виконує одночасно роль трансформатора, напруга у вторинній – вимірювальній обмотці якого збільшується при розміщенні в ній феромагнітного зразка.
Експериментальна установка
Рис.13.3. Схема експериментальної установки.
Очевидно, що при температурі, близькій до точки Кюрі, коли магнітна проникність залізного осердя різко знизиться, магнітний потік Ф зменшиться, а відповідно зменшиться і напруга U вим., що дорівнює ℰ втор. Вимірюючи U вим при нагріванні феромагнітного сердечника можна зафіксувати момент переходу феромагнетика в парамагнетик. Температура феромагнетику вимірюється проградуйованою термопарою. Термопара, це сплав двох різнорідних провідників П1 та П2. При нагріванні точки сплаву електрони, у яких від нагрівання збільшується енергія, переходять, наприклад, з провідника П1 в провідник П2. За законом збереження заряду провідник П1 заряджається позитивно, а П2 – негативно, оскільки в ньому стає більше електронів. Між провідниками П1 та П2 виникає термо – Е.Р.С., яка строго пропорційна температурі нагріву сплаву. Якщо проградуювати таку термопару по Т 1 = 100°С (кипляча вода) та Т 2 = 0°С (лід), можна використовувати зазначений пристрій для вимірювання температури. Завдання 1. Скласти схему (рис.13.3). 2. Визначити кімнатну температуру та встановити на гальванометрі значення, яке відповідає цій температурі. Для цього використати калібрувальну криву термопари. 3. Увімкнути піч, зняти залежність показів вольтметра від температури. Спочатку виміряти напругу U вим через кожні 500С. При температурі, близькій до точки Кюрі, слід вимірювати U вим частіше. Для цього в момент різкого спаду U вим, що відповідає точці Кюрі, вимкнути піч та зачекати, доки зразок охолоне на 20 – 25 0С. Після цього знову провести повторні вимірювання, частіше вимірюючи температуру. 4. Прогріти феромагнітний зразок до температури, яка перевищує точку Кюрі на 50 – 100 0С та прослідкувати зміну напруги U вим. 5. Побудувати залежність U вим (Т) зразка. Екстраполюючи отриману криву, визначити точку Кюрі феромагнетику.
Дані вимірювання занести у таблицю:
Контрольні запитання
1. Яка структура феромагнетика? 2. Пояснити явище втрати феромагнітних властивостей при нагріванні зразка до температури Кюрі і вище. 3. Чому дорівнює магнітний момент струму? 4. Як визначити енергію контуру зі струмом? 5. Дайте означення намагніченості речовини. Як залежить намагніченість діа- і парамагнетиків від величини зовнішнього магнітного поля? 6. Як залежить c-1 для феромагнетиків від температури? Поясніть особливості цієї залежності. 7. Як залежить c-1 для пара магнетиків від температури? 7. Дайте означення температури Кюрі.
Література.
1. Сивухин Д.В. Общий курс физики. - М.: Наука, 1983. 2. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л.- М.: Наука, 1983. 3. Парсел Е. Электричество и магнетизм. - М.: Наука, 1983, гл. 4, п. 4 - 6; гл. 6, п. 9..
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


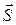 , який співпадає з нормаллю до площини контуру за напрямком та має модуль, рівний площині S. Тоді:
, який співпадає з нормаллю до площини контуру за напрямком та має модуль, рівний площині S. Тоді: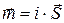 . (13.1)
. (13.1)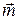 , від індукції зовнішнього поля
, від індукції зовнішнього поля 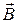 та від кута між ними. Можна показати, що ця енергія дорівнює:
та від кута між ними. Можна показати, що ця енергія дорівнює: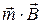 . (13.2)
. (13.2) . По визначенню
. По визначенню  (13.3)
(13.3) у відсутності зовнішнього поля обертається в нуль, а при його наявності - пропорційний напруженості цього поля:
у відсутності зовнішнього поля обертається в нуль, а при його наявності - пропорційний напруженості цього поля: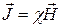 .
.
 , чи -
, чи -  ½. (13.4)
½. (13.4)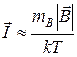 (13.7)
(13.7) , або
, або  ,(13.9)
,(13.9)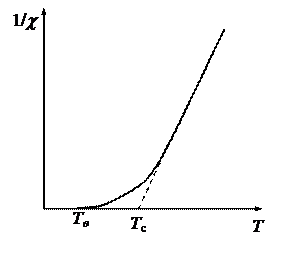
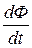 , оскільки в обмотці протікає змінний струм. Цей змінний магнітний потік перетинає витки вторинної обмотки. За законом електромагнітної індукції в провідниковому контурі, який перетинається змінним магнітним потоком, генерується електрорушійна сила – Е.Р.С. індукції. Електрорушійна сила змушує рухатись в контурі електрони, що приводять до виникнення в ньому різниці потенціалів.
, оскільки в обмотці протікає змінний струм. Цей змінний магнітний потік перетинає витки вторинної обмотки. За законом електромагнітної індукції в провідниковому контурі, який перетинається змінним магнітним потоком, генерується електрорушійна сила – Е.Р.С. індукції. Електрорушійна сила змушує рухатись в контурі електрони, що приводять до виникнення в ньому різниці потенціалів.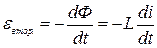 ,
,



