
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 1. Основні поняття та визначенняСодержание книги Поиск на нашем сайте
Розділ 1. ОСНОВНІ ПОНЯТТЯ ТА ВИЗНАЧЕННЯ Теорія надійності як наука оперує такими основними поняттями та визначеннями. Надійність — це властивість виробу (деталі, приладу, системи) виконувати задані функції, зберігаючи свої експлуатаційні показники в заданих межах, при певних режимах і умовах експлуатації, протягом необхідного часу чи необхідного об'єму виконаної виробом роботи. Об'єм роботи виробу (кілометри, гектари, кубометри) чи тривалість функціонування виробу (години, цикли) характеризують таке поняття в теорії надійності як наробка. Працездатність — властивість виробу виконувати задані функції з параметрами і характеристиками, які відповідають технічній документації. Властивість виробу зберігати працездатність (тобто не мати відмов) протягом заданого часу і при визначених умовах експлуатації називається безвідмовністю. Відмова — подія, після якої виріб перестає виконувати (цілком або частково) свої функції, або, інакше кажучи, — це подія, яка спричиняє перехід виробу з працездатного стану в непрацездатний. Відмови можна класифікувати за цілим рядом ознак (табл. 1). Пояснимо, що розуміють під тим чи іншим видом відмови, Повні (катастрофічні) відмови — це такі відмови, при яких прилад втрачає працездатність (короткі замикання в електричних колах, поломки, заїдання і деформації механічних деталей, згорання чи розплавлений деталей конструкції і компонентів схем). Часткові (параметричні) відмови — це погіршення якості функціонування виробу. Якщо погіршення якості функціонування виробу не призводить до відмови, то такі несправності називають дефектами, і їх розгляд виходить за межі теорії надійності.
Класифікація відмов Tаблиця 1
Класифікація відмов на раптові і поступові до деякої міри умовна, тому що появі раптової відмови, здебільшого, передують скриті зміни властивостей елементів, які не вдається проконтролювати. Такі типи відмов, як залежна і незалежна, або стійка і тимчасова, не потребують додаткового пояснення, тому що суть відмови повністю виражена в її назві. У теорії надійності розрізняють два класи виробів:невідновлювані (не ремонтовані), тобто такі, які не підлягають ремонту у випадку відмови, і відновлювані, тобто ремонтопридатні. До перших належать переважно елементи складних виробів — деталі радіоелектронної апаратури, машин і приладів. Деякі пристрої можна розглядати як невідновлювані за одних умов і відновлювані за інших (наприклад, бортові пристрої ракет або штучних систем в космосі невідновлювані в польоті і відновлювані при підготовці до стартів). Зауважимо, що надійність невідновлюваного виробу насамперед визначається його безвідмовністю. Довговічність виробу — це здатність до довготривалої експлуатації при необхідному технічному обслуговуванні, до якого можуть входити різні види ремонтів. Ремонтопридатність — це пристосовуваність виробу до попередження, знаходження і ліквідації відмови. Ресурс — наробкадо критичного стану, який регламентується технічною документацією. Цей показник властивий виробам з особливо відповідальними функціями (літальні пристрої, системи;атомної енергетики тощо). Елемент розрахунку надійності — це пристрій (деталь, елемент, прилад, лінія або канал зв'язку, система або комплекс' систем), який входить до розрахунку надійності окремою! самостійною частиною, що має свій загальний кількісний показник надійності. Виріб — це будь-який предмет, чи сукупність предметів виробництва, які виробляються підприємством. Виробами можуть бути деталі, збірні модулі, комплекси і комплекти. Система — це виріб, який складається з комплектуючих частин, що об'єднані або не об'єднані збірними операціями, і призначений для виконання певних функцій. Система може представляти собою не тільки сукупність комплектуючих технічних засобів, але й мати в своєму складі і нетехнічні засоби, наприклад, програмне забезпечення, людину-оператора та інше. Об'єкт — це предмет цільового призначення, який розглядається в період проектування, виробництва, експлуатації, вивчення, дослідження чи випробування на надійність. Об'єктами можуть бути як системи, так і їх елементи. В теорії надійності розглядають три найбільш вживані показники надійності: — ймовірність безвідмовної роботи протягом заданого часу; — середній час напрацювання до відмови; — коефіцієнт готовності виробу. Знаходження цих показників для різних теоретичних розподілів випадкових величин, що характеризують надійність виробів, буде розглянуто в наступних розділах. Неремонтовані вироби працюють до першої відмови. Цілий ряд показників надійності неремонтованих об'єктів є характеристиками випадкової величини — часу наробки виробу до відмови. Під часом наробки до відмови розуміють тривалість роботи виробу. Для великої кількості виробів, які випробуються, цей показник є різним і носить випадковий характер, а його середньоквадратичне відхилення називається дисперсією.
Розділ 2. ТЕОРЕТИЧНІ АСПЕКТИ РОЗРАХУНКУ НАДІЙНОСТІ
Закони розподілу У розділі 2.2 введено поняття «крива розподілу часу наробки до відмови», тобто залежність f(t). Ця залежність може служити математичною моделлю надійності виробу, необхідною для теоретичної оцінки надійності окремого елемента чи системи в цілому. Зрозуміло, що спектр різновидів функцій f(t) буде дуже широким, оскільки вони відбивають особливості фізичних процесів, властивих саме тому чи іншому виробові. Маючи криву розподілу наробки до відмови, визначають всі інші характеристики надійності. З урахуванням (2.18) можна стверджувати, що кривою розподілу може бути будь-яка лінія, площа під якою дорівнює одиниці. Як свідчать численні дослідження, надійність більшості виробів може бути змодельована певною сукупністю функцій, які ми розглянемо далі. Вони дають змогу описати величину f(t) з максимальним наближенням до тих залежностей f'(t), які відбивають реальну природу виробів. Це є розподіли Вейбула, гама-розподіл та їх окремі випадки, якими дуже часто користуються, нормальний розподіл, логарифмічно-нормальний, альфа-розподіл, розподіл Релея, трикутний розподіл тощо. Коротке пояснення аналітичних виразів законів розподілів і області їх застосування в теорії надійності почнемо з розподілу Вейбула [З]. У цьому випадку
де С — параметр масштабу, який «стискає», чи «розтягує» криву; b — параметр форми розподілу, який стискає його асиметрію і ексцес. Графіки функції розподілу Вейбула показані на рис.2.4. Запишемо ймовірність безвідмовної роботи для даного випадку
Рис.2.4. Графіки розподілу Вейбула при С=1 у випадках b = 0,5 (крива 1), b = 1 (крива 2), b = 1.5 (крива 3), b = 2 (крива 4), b = 4 (крива 5). Своєю чергою інтенсивність відмов матиме вигляд:
Вирази (2.52) і (2.53) графічно зображені на рис.2.5.
Рис.2.5. Криві інтенсивності відмов та ймовірності безвідмовної роботи при розподілі Вейбула. Середній час наробки до відмови Тм розраховують таким чином:
де Розподіл Вейбула використовують для отримання математичної моделі надійності деякого механічного обладнання, зокрема, підшипників, які застосовують в електричних двигунах, а також для окремих типів електронних ламп (р= 1,4¸1,7). Перевагою розподілу Вейбула є велика кількість форм кривих, які можна отримати. Це дає змогу використовувати даний закон розподілу для більш широкого класу електрооб- ладнання, ніж вказано вище, в початковий період експлуатації (період приробки). Наступною моделлю густини розподілу часу наробки до відмови є гама-розподіл. У цьому випадку згадана густина розподілу має вигляд:
Такий розподіл також задається двома параметрами: b — параметр масштабу; a — параметр форми розподілу. Графічне зображення f(t) для гама-розподілу показано на рис.2.11. Середній час наробки до відмов у цьому випадку визначають як TM =a/b. У теорії надійності гама-розподіл використовується при цілих значеннях a. Тоді гама-розподіл називається розподілом Ерланга [4]. Для розподілу Ерланга запишемо
Ймовірність безвідмовної роботи та інтенсивність відмов матиме вигляд
Рис. 2.6. Гама-розподіл при різних параметрах a.
Графіки залежностей f(t),P(t),l(t) для розподилу Ерланга показані нав рис.2.7
Рис.2.7. Графіки функцій при розподілі Ерланга (l>1). Розподіл Ерланга другого порядку (b = 1, l = 2/Тв) широко використовують для моделювання розподілу часу відновлення систем електроприводів. Це пояснюється тим, що час відновлення tв складається з двох частин: tВ=to+tp (2.59) де to — час, затрачений на пошук несправностей; tp — час, затрачений на ремонт. Якщо припустити, що випадкові величини to і tp розподілені за експоненційним законом ((2.62) — (2.64)) з однаковими середніми значеннями ТB/2, то густина ймовірності величини tB, яка є комбінацією to і tp відповідності з відомими положеннями теорії ймовірності:
Залежність f(tB), побудована у відповідності з (2.60), відповідає графіку на рис.2.12 при l > 1, тобто має вигляд густини розподілу Ерланга. Критерій ремонтопридатності — ймовірність відновлення системи за tзв буде у відповідності з (2.49) дорівнювати:
Гама-розподіл також має великий спектр кривих. Особливістю такого розподілу є те, що сума n незалежних випадкових величин, кожна з яких підпорядковується гамарозподілу з параметрами a і b,також має гама-розподіл з параметрами b і Розглянемо окремий випадок розподілу Вейбула (при a = 1) та гама-розподілу Ерланга (при b =1) — експоненційний розподіл. Цей розподіл часу наробки до відмови характеризується виразами f(t), P(t), l(t). l(t) = l = const, (2.62) f(t)=l exp(-lt), (2.63) P(t)=exp(-lt). (2.64) Такий закон розподілу ще називають показниковим. Графіки функцій f(t), l(t) і P(t) при експоненційному законі розподілу показані на рис.2.8. .
Рис2.8. Графіки екпоненціального закону росподілу. Наведений закон розподілу використовують доволі часто, оскільки він придатний для опису характеристик надійності склад них електромеханічних систем, навіть якщо елементи цих систем мають різноманітні закони розподілу. Це пояснюється тим, що більшість виробів проходить «тренування» безпосередньо після виготовлення в заводських умовах і до споживача вони надходять при стабільно низьких значеннях інтенсивностей відмов. Завдяки цьому споживач працює з виробами, які мають більш-менш постійні величини l. Експоненційний розподіл також набув широкого поширення через простоту формул для розрахунку характе ристик надійності. При недостатній кількості статистичних дант складно виявити відхилення від виразу l = const, навіть якщо такі відхилення і відбувається. У цьому випадку постійне значення інтенсивності відмов можна прийняти як перше наближення при розрахунках. У той же час, якщо вироби не пройшли «тренування»на виробництві в початковий період експлуатації, розподіл часу наробки до відмови потребує іншої математичної моделі. Такою моделлю може бути нормальний закон розполілу. Цей розподіл ще називають розподілом Гаусса. Оскільки час наробки до відмови набуває тільки додатних значень, то в теорії надійності йдеться про зрізаний нормальний розподіл. Зрізаний нормальний розподіл отримують з нормального, обмежуючи інтервал значень випадкової величини часу наробки до відмови t1 ¸ t2. Тоді запишемо густину зрізаного нормального розподілу f(t)=C· f(t), (2.65) де С — нормуючий множник, який забезпечує нормування кривої розподілу, тобто
Підставимо в (2.66) вираз для f(t) і, застосувавши позначення
де TM- середній час наробки до відмови; s— середнє квадратичне відхилення часу наробки до відмови для незрізаного розподілу, після перетворень отримаємо:
де Таблиця значень цієї функції наведена в додатку 2. У випадку 0 < t < ¥ (а саме цій умові відповідає зрізаний нормальний розподіл) отримаємо такі вирази для функцій: а) де б) в) г) де
На рис. 2.9 наведені залежності відношення числових характеристик зрізаного і незрізаного нормального розподілу і значені нормуючого множника С від співвідношення Тм /s.
Рис.2.9. Залежність відношення числових характеристик зрізаного і незрізаного нормального розподілу (риска над Як видно з рис.2.9. при Графічне зображення f(t), l(t), P(t) для зрізаного розподілу показано на рис.2.10.
Рис.2.10. Функціональні залежності при нормальному законі розподілу. Необхідно відзначити, що умовою нормального розподіл наробки до відмови є малий розкид значень швидкостей зношування елементів, тому що саме поява відмов за рахунок зношування елементів найкраще моделюється нормальним законом розподілу. Бувають випадки явно несиметричних розподілів часу наробки до відмови. Тоді за модель f(t) беруть логарифмічний нормальний закон розподілу. Логарифмічний нормальний (логнормальний) розподіл задається густиною розподіл
де m — середнє значення випадкової величини t; s — середньоквадратичне відхилення величини ln t. Ймовірність безвідмовної роботи розраховують за такої формулою [14].
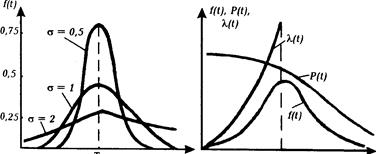
Рис.2.11. Криві густини при логарифмічному нормальному законі розподілу. Криві густини логнормальног розподілу наведені на рис.2.11. Дослідження, виконані в роботі [14] показують, що логнормальний закон розподілу часу відновлення (ремонту) характерний для випадків, коли системі керування електроприводами ремонтують, замінюючи несправні елементи, безпосередньо на міці де працює електропривод. Якщо у час відновлення входить такоз час пошуку несправностей і безпосередньо ремонт, то кращою математичною моделлю є окремий випадок — розподіл Ерланга другого порядку. Розглянемо ще декілька законів розподілу, які можуть використовуватись для побудови математичних моделей надійності. Розполіл Релея описують виразами [4];
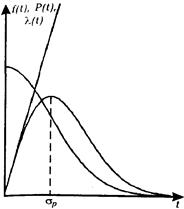
Рис.2.12. Графічні залежності розподілу Релея.
f(t)=t/s2exp[-t2/(2sp2)] (2.75)
де sр — параметр розподілу Релея, який є модою розподілу (значення t, яке відповідає екстремуму функції) і його не слід плутати зі середньоквадратичним відхиленням. Для розподілу Релея математичне сподівання (середній час наробки до відмови)
а дисперсія
Графіки функцій розподілу Релея показані на рис.2.12. Трикутний розподіл характеризує випадкові величини, які мають обмежену область можливих значень (tn, tk) Цей розподіл (рис.2.13) описують такі три параметри: tn, tk — межі допустимих значень, tm — мода. Якщо позначити f(tm)= h то з визначення площі трикутника отримаємо: 0.5h(tn- tk)=1 (2.80) З виразу (2.80) отримаємо h=2/(tn- tk) (2.81)
Puc.2.13. Графічні залежності при трикутному розподілі. Тоді запишемо густину розподілу f(t) з урахуванням (2.81) Ймовірність безвідмовної роботи матиме вигляд:
Інтенсивність відмов для трикутного розподілу буде такою:
Біноміальний розподіл. Цей дискретний розподіл описує появу подій, які мають два значення, що взаємно виключають одне одного. Якщо, наприклад, в партії із 100 виробів 90 справних, а 10 бракованих, то ймовірність появи цих виробів становить 0,9 справних і 0,1 — бракованих. Очевидно, що коли в певну сукупність однакових виробів входять справні вироби, відносна частка яких становить р і браковані, відносна частка яких становить q, то p+q=l. Якщо з великої партії однакових виробів з q % несправних, береться вибірка в кількості n, то ймовірності появи різної кількості несправних виробів в цих вибірках визначаються коефіцієнтами розкладання членів біноміального ряду (Р + q)n =1 або
де q=q%/100% — частка одиниці несправних виробів в партії, а р — частка справних. У рівнянні (2.85) рn показує ймовірність відсутності несправних виробів у вибірці об'ємом n зразків, другий член npn-1q дає ймовірність появи у вибірці одного несправного виробу, третій член Приклад 2.1. З великої партії сельсинів типу НС-404, в якій є q % =5% несправних зразків, береться для використання в системі вибірка з чотирьох машин (n=4). Визначити ймовірність появи у вибірках О, 1, 2, 3 чи 4 несправних сельсини. Розв'язування.
Тоді ймовірність появи у вибірці 0 несправних сельсинів: p4=(0.95)4=0.8145. Ймовірність появи у вибірці 1 несправного сельсина: 4pзq=4×(0,95)3×0,05=0,1715. Ймовірність появи у вибірці 2 несправних сельсинів: 6p2q2=6×(0.95)2×(0.05)2=0.0136. Ймовірність появи у вибірці 3 несправних сельсинів: 4pqз=4×(0,95)×(0,05)3=0,0004. Ймовірність появи у вибірці 4 несправних сельсинів: q4=(0,05)4=0,0000. Повна ймовірність дорівнює 1,000. Розподіл Пуассона. У випадку дискретного розподілу Пуассона розглядають події, ізольовані в часі чи просторі. Так, кількість відмов у роботі якоїсь системи протягом деякого проміжку часу характеризує появу ізольованих в часі подій. Розподіл Пуассона, як і біноміальний, також складається з ряду членів, кожен з яких відповідно визначає ймовірність появи О, 1, 2, 3 чи більшої кількості подій на одиницю вимірювання. При цьому сума цих ймовірностей дорівнює одиниці. Розподіл Пуассона записують таким чином
де а- середня кількість несправних виробів, або несправностей на вибір при вибірці об¢ємом n. Величина а визначається як добуток об¢єму вибірки n на середнє значення частки кількості несправностей на вибір,або частки несправних виробів у цілій партії q¢,тобто ф=nq¢ при цьому
або
У виразі (2.86) кожен член лівої частини означає: e-a - ймовірність появи 0 несправностей на виріб, або несправних виробів у вибірці; ae-a - ймовірність появи 1 несправності на вибір, або несправного виpобу у вибірці;
Розподіл Пуассона зручно використовувати, наприклад, при контролі якості виробів. Він визначає основу для складання плану вибіркового прийому виробів у відділах технічного контролю підприємства. Розподіл Пуассона при Ь = 0 і a =lt перетворюється в експоненційний закон розподілу. Отже, експоненційний закон розподілу є окремим випадком закону розподілу Пуассона. Лямбда-характеристика У розділі 2.3 розглянуто різноманітні математичні моделі надійності. Завданням дослідника є підбір такого закону розподілу, який би забезпечував адекватність моделі процесам відмови виробу. У той же час можливі ситуації, коли експериментальні залежності f(t),l(t) не підпадають ні під один відомий закон розподілу протягом часу функціонування системи чи окремого елемента. Тоді користуються експериментальними кривими, зокрема, залежністю інтенсивності відмов від часу, для оперативного прийняття рішень з підвищення надійності. Така залежність називається лямбда-характеристикою (l-характеристика). Лямбда-характеристика дає змогу виявити деякі особливості і недоліки експлуатації технічних пристроїв, тобто вона вказує на необхідність проведення тих чи інших заходів щодо забезпечення потрібного рівня надійності. Типова l-характеристика показана на рис.2.14. Можна відзначити три характерні її ділянки: І — період припрацьовування з високим рівнем інтенсивності відмов, коли очевидно ненадійні елементи (або елементи з прихованими дефектами) швидко відмовляють; II — період нормальної роботи, коли на інтенсивність відмов впливають різноманітні випадкові чинники, але сама інтенсивність відмов залишається постійною і мінімальною; III — період старіння, під час якого лавиноподібне зростає інтенсивність відмов, і зумовлений цей процес зношуванням та старінням елементів.
Рис.2.14. Типова l-характеристика. За аналогією з життям людини напрошуються такі визначення періодів l-характеристики: І — «дитинство», II — «зрілість», і — «старість». З точки зору забезпечення надійної роботи вироб необхідно його експлуатувати в період «зрілості». Для забезпечеі ня тривалішого цього періоду необхідно скоротити період «дитинства». Цього досягають шляхом припрацювання і тренуванн пристроїв на заводі в умовах, близьких до експлуатаційних. Швидкість переходу з періоду І в період II може служти опосередкованим показником культури виробництва. Чим вища якість виготовлення і перевірки елементів, тим більш однорідною є продукція, і тим швидше падає інтенсивність відмов, зумовлені виробничими причинами (поганий монтаж, неякісне лютування тощо). При погіршенні якості виготовлення пристрою період «дитинства» збільшується і перехід до періоду II стає дуже плавним. При цьому «тренування» часто стає нераціональним. Необхідно відзначити, що l-характеристики систем не завжди мають такий вигляд, як на рис.2.14. Вони можуть відрізнятися від наведеної кривої тому, що складові систем мають різну механічі і електричну міцність та різні l-характеристики. Цим зумовлена поява локальних екстремумів (максимумів) на характеристиці наприклад, як це показано на рис.2.15.
рис.2.15.l-характеристика ситеми. Поява екстремуму в інтервалі t1...t2 вказує на необхідність сумлінної перевірки конструкції, матеріалів, елементів і технології виготовлення для того, щоб з'ясувати причини збільшення інтенсивності відмов. Якщо його усунути не вдається, то з допомогою організаційних заходів слід вилучити систему з експлуатації протягом часу t1-t2 і перевести й на стендові випробування. Тривалість таких випробувань має становити якраз час t2- t1. Після цього систему можна повернути для нормальної експлуатації. До переваг експлуатації в період «зрілості» належить також і простота розрахунків, тому що цей період характеризується сталою інтенсивністю відмови, тобто діє експоненційний закон розподілу. Необхідно відзначити, що в період припрацювання відмови приблизно підпорядкову- ються розподілу Вейбула, а в період старіння - нормальному розподілу.
Приклад 4.4 У силовому блоці керування електродвигуном застосовано пасивне розділене дублювання резисторів, кожен з яких має опір R. Схема допускає зміну опору резисторної комірки на величину R.Допустима ймовірність відмови однієї резервованої комірки присторів Q(tі) = 6* 10-6 1/год протягом часу t = 80 год. Визначити, якою повинна бути інтенсивність відмов одного резистора l0, якщо при відмові одного резистора інтенсивність другого, внаслідок підвищення навантаження, змінюється на третину і дорівнює l1=4/3l0. Розв'язування Електрична схема з'єднання резисторів показана на рисунку
Логічна схема для розрахунку надійності, яка відповідає наведеному електричному з'єднанню, показана на рисунку
У даному випадку скористаємося виразом (4.21), в якому m = 2. Отримаємо
Ураховуючи, що
Отримаємо
Оскільки
Розділ 1. ОСНОВНІ ПОНЯТТЯ ТА ВИЗНАЧЕННЯ Теорія надійності як наука оперує такими основними поняттями та визначеннями. Надійність — це властивість виробу (деталі, приладу, системи) виконувати задані функції, зберігаючи свої експлуатаційні показники в заданих межах, при певних режимах і умовах експлуатації, протягом необхідного часу чи необхідного об'єму виконаної виробом роботи. Об'єм роботи виробу (кілометри, гектари, кубометри) чи тривалість функціонування виробу (години, цикли) характеризують таке поняття в теорії надійності як наробка. Працездатність — властивість виробу виконувати задані функції з параметрами і характеристиками, які відповідають технічній документації. Властивість виробу зберігати працездатність (тобто не мати відмов) протягом заданого часу і при визначених умовах експлуатації називається безвідмовністю. Відмова — подія, після якої виріб перестає виконувати (цілком або частково) свої функції, або, інакше кажучи, — це подія, яка спричиняє перехід виробу з працездатного стану в непрацездатний. Відмови можна класифікувати за цілим рядом ознак (табл. 1). Пояснимо, що розуміють під тим чи іншим видом відмови, Повні (катастрофічні) відмови — це такі відмови, при яких прилад втрачає працездатність (короткі замикання в електричних колах, поломки, заїдання і деформації механічних деталей, згорання чи розплавлений деталей конструкції і компонентів схем). Часткові (параметричні) відмови — це погіршення якості функціонування виробу. Якщо погіршення якості функціонування виробу не призводить до відмови, то такі несправності називають дефектами, і їх розгляд виходить за межі теорії надійності.
Класифікація відмов Tаблиця 1
Класифікація відмов на раптові і поступові до деякої міри умовна, тому що появі раптової відмови, здебільшого, передують скриті зміни властивостей елементів, які не вдається проконтролювати. Такі типи відмов, як залежна і незалежна, або стійка і тимчасова, не потребують додаткового пояснення, тому що суть відмови повністю виражена в її назві. У теорії надійності розрізняють два класи виробів:невідновлювані (не ремонтовані), тобто такі, які не підлягають ремонту у випадку відмови, і відновлювані, тобто ремонтопридатні. До перших належать переважно елементи складних виробів — деталі радіоелектронної апаратури, машин і приладів. Деякі пристрої можна розглядати як невідновлювані за одних умов і відновлювані за інших (наприклад, бортові пристрої ракет або штучних систем в космосі невідновлювані в польоті і відновлювані при підготовці до стартів). Зауважимо, що надійність невідновлюваного виробу насамперед визначається його безвідмовністю. Довговічність виробу — це здатність до довготривалої експлуатації при необхідному технічному обслуговуванні, до якого можуть входити різні види ремонтів. Ремонтопридатність — це пристосовуваність виробу до попередження, знаходження і ліквідації відмови. Ресурс — наробкадо критичного стану, який регламентується технічною документацією. Цей показник властивий виробам з особливо відповідальними функціями (літальні пристрої, системи;атомної енергетики тощо). Елемент розрахунку надійності — це пристрій (деталь, елемент, прилад, лінія або канал зв'язку, система або комплекс' систем), який входить до розрахунку надійності окремою! самостійною частиною, що має свій загальний кількісний показник надійності. Виріб — це будь-який предмет, чи сукупність предметів виробництва, які виробляються підприємством. Виробами можуть бути деталі, збірні модулі, комплекси і комплекти. Система — це виріб, який складається з комплектуючих частин, що об'єднані або не об'єднані збірними операціями, і призначений для виконання певних функцій. Система може представляти собою не тільки сукупність комплектуючих технічних засобів, але й мати в своєму складі і нетехнічні засоби, наприклад, програмне забезпечення, людину-оператора та інше. Об'єкт — це предмет цільового призначення, який розглядається в період проектування, виробництва, експлуатації, вивчення, дослідження чи випробування на надійність. Об'єктами можуть бути як системи, так і їх елементи. В теорії надійності розглядають три найбільш вживані показники надійності: — ймовірність безвідмовної роботи протягом заданого часу; — середній час напрацювання до відмови; — коефіцієнт готовності виробу. Знаходження цих показників для різних теоретичних розподілів випадкових величин, що характеризують надійність виробів, буде розглянуто в наступних розділах. Неремонтовані вироби працюють до першої відмови. Цілий ряд показників надійності неремонтованих об'єктів є характеристиками випадкової величини — часу наробки виробу до відмови. Під часом наробки до відмови розуміють тривалість роботи виробу. Для великої кількості виробів, які випробуються, цей показник є різним і носить випадковий характер, а його середньоквадратичне відхилення називається дисперсією.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.024 с.) |

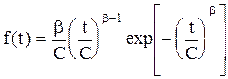 (2.51)
(2.51)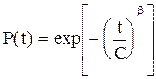 (2.52)
(2.52)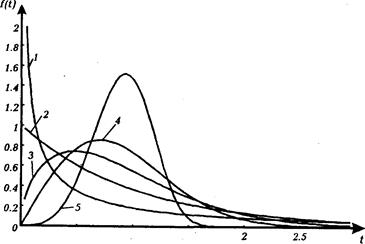
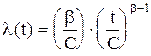 (2.53)
(2.53)
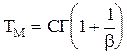 (2.54)
(2.54) - гама-функція, яку знаходять за таблицями в додатку 1.
- гама-функція, яку знаходять за таблицями в додатку 1.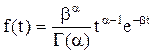 , a,b >0, t>0 (2.55)
, a,b >0, t>0 (2.55) (2.56)
(2.56)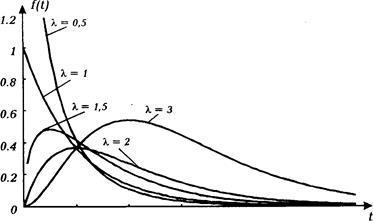
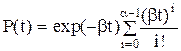 (2.57)
(2.57) (2.58)
(2.58)
 (2.60)
(2.60) (2.61)
(2.61)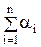

 - густина нормального розподілу;
- густина нормального розподілу; , звідки
, звідки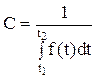 (2.66)
(2.66)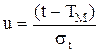 ,
, (2.67)
(2.67) — нормальна функція Лапласа.
— нормальна функція Лапласа.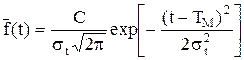 (2.66)
(2.66)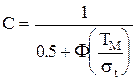
 (2.69)
(2.69) (2.70)
(2.70)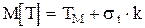 (2.71)
(2.71)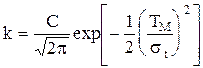
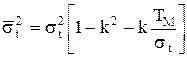 (2.72)
(2.72)
 і
і 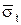 означає, що ці характеристики належать до зрізаного розподілу).
означає, що ці характеристики належать до зрізаного розподілу).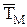 /
/ 
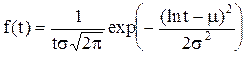 (2.73)
(2.73)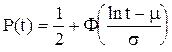 (2.74)
(2.74)
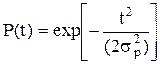 (2.76)
(2.76)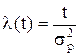 (2.77)
(2.77) (2.78)
(2.78)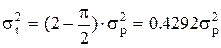 (2.79)
(2.79)
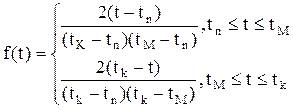 (2.82)
(2.82)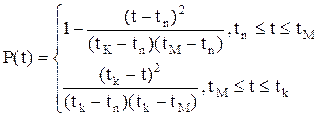 (2.83)
(2.83)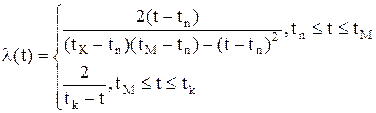 (2.84)
(2.84) pn+npn-1q+n(n-1)pn-2q2/2!+n(n-1)(n-2)pn-3q3/3!+...+qn=1 (2.85)
pn+npn-1q+n(n-1)pn-2q2/2!+n(n-1)(n-2)pn-3q3/3!+...+qn=1 (2.85) — ймовірність появи у вибірці двох несправних виробів тощо, останній член qn визначає ймовірність появи у вибірці n несправних елементів.
— ймовірність появи у вибірці двох несправних виробів тощо, останній член qn визначає ймовірність появи у вибірці n несправних елементів.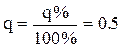 ; q =1-0.05 = 0.95. При цьому (p+q)4= 1.
; q =1-0.05 = 0.95. При цьому (p+q)4= 1. (2.86)
(2.86)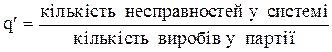
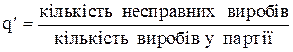
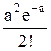 -ймовірність появи 2 несправностей на вибір, або двох несправних виробів у вибірці;
-ймовірність появи 2 несправностей на вибір, або двох несправних виробів у вибірці;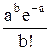 - ймовірність появи Ь несправностей на виріб, або b несправних виробів у вибірці.
- ймовірність появи Ь несправностей на виріб, або b несправних виробів у вибірці.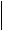






 t t
t t
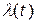

 t1 t2 t
t1 t2 t

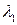

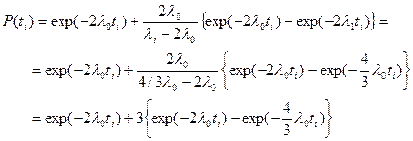
 , при наступних перетвореннях отриманого виразу доцільно скористатися розкладанням в ряд показникової функції, обмежившись трьома його першими членами:
, при наступних перетвореннях отриманого виразу доцільно скористатися розкладанням в ряд показникової функції, обмежившись трьома його першими членами: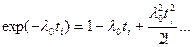

 , то інтенсивність відмов одного резистора не повинна перевищувати
, то інтенсивність відмов одного резистора не повинна перевищувати



