
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логічне з'єднання зіркою і трикутникомСодержание книги Поиск на нашем сайте Логіко-ймовірнісний метод дає змогу розрахувати ймовірність безвідмовної роботи практично для будь-якої логічної схеми з'єднань елементів. Слід тільки відзначити, що при цьому може бути отриманий дуже громіздкий вираз логічної функції працездатності, з якою не дуже зручно працювати. Основною перешкодою до зведення будь-якої логічної схеми до логічного послідовного і паралельного з'єднання є логічні з'єднання «зірка» і «трикутник» («дельта»). Через наявність таких з'єднань і доводиться користуватися логіко-ймовірнісним методом. Розглянемо можливість еквівалентної заміни «зірки» на «трикугник» і навпаки. Завдяки такій заміні з'являється можливість приведення логічних схем до логічного послідовного і паралельного з'єднання. Розглянемо «зірку» і «трикутник», які показані на рис.3.5.
Рис.3.5. Логічне з'єднання «трикутник» і «зірка». Позначимо елементи «трикутника» АВ, ВС, АС, а елементи «зірки» А, В, С, причому вершини «трикутника» і «зірки» V1, V2, V3 залишаються без змін. Еквівалентність заміни означає, що ймовірність безвідмовної роботи системи з логічним з'єднанням «трикутник» є такою самою, як і системи з логічним з'єднанням «зірка». Розглянемо три випадки: а) входом системи є вершина V1, а виходом V3 ; б) входом системи є вершина V2 а виходом V3; в) входом системи є вершина V1, а виходом V2. Ймовірність безвідмовної роботи для випадку а) при з'єднанні «зіркою» визначимо як PА(t)РС(t). Для з'єднання «трикутником» ймовірність безвідмовної роботи розраховується як PAC(t)+PAB(t)PBC(t)-PAC(t)PAB(t)PBC(t) (див.вираз (3.9). Оскільки ймовірність безвідмовної роботи в обох випадках повинна бути однаковою, то запишемо PA(t)PC(T)=PAC(t)+PAB(t)PBC(t)-PAB(t)PBC(t)PCA(t) (3.14) Аналогічним чином запишемо рівняння і для випадку б) і в) PB(t) PC(t)= PBC(t)+ PAB(t) PAC(t)- PAB(t)PBC(t) PCA(t) (3.15) PA(t) PB(t)= PAB(t)+ PCA(t) PBC(t)- PAB(t) PBC(t) PCA(t) (3.16) Введемо такі позначення: PBC(t)=x1; PAC(t)= x2; PAB(t)= x3; PA(t)=a; PB(t)=b; PC(t)=c Тоді рівняння (3.14)—(3.16) перепишемо так: bc = Е1 = х1 + x2 • x3 -x1 • x2 • x3; ас = E2 = x2 + x1 • x3 -x1 • x2 • x3; (3.17) ab = E3 = x3 + x2 • x2 - x1 • x2 • x3 В результаті перемноження одержимо abc= Розділивши рівняння (3.18) по черзі на кожне з рівнянь, системи (3.17), запишемо формули еквівалентних перетворень у вигляді: а=Е4/Е1, (3.19) b=E4/E2, (3.20) с=Е4/Е3. (3.21) Приклад 3.3 Нехай ймовірності безвідмовної роботи елементів, з'єднаниз в «трикутник», становлять: х1= 0,7; х.2= 0,8; х3 = 0,9. Визначита параметри надійності еквівалентної «зірки». Розв'язування Визначимо Е1, Е2, Е3, Е4 відповідності з виразами (3.17) і (3.18) Е1= х1 + х.2х3 - х1х.2х3 = 0,7 + 0,8 • 0,9 + 0,7 • 0,8 • 0,9 = 0,916, E2 = х.2+ х1х3- х1х.2х3 = 0,8 + 0,7 • 0,9 + 0,7 • 0,8 • 0,9 = 0,926, E3= х3 + х1х2- х1х.2х3= 0,9 + 0,7 • 0,8 + 0,7 • 0,8 0,9 = 0,956.
Використовуючи вираз (3.19) — (3.21), знайдемо ймовірність безвідмовної роботи еквівалентної зірки. a = РА(t) = Е4/Е1 =0,900497 / 0,916 = 0,983075, b = PB(t) = Е4/Е2 =0,900497 / 0,926 = 0,972458, c = PC (t) = E4/E3 =0,900497 / 0,956 = 0,941942. Для здійснення зворотного переходу від «зірки» до «трикутника» знову ж таки слід скористатися системою рівнянь (3.17), в якій відомі величини a, b, c, a невідомі х1, х2, х3. Це означає, що слід розв'язати систему рівнянь (3.17) відносно х1, х2, х3. Як свідчать виконані дослідження, аналітичний вираз х1, х2, х3 практично отримати неможливо. Тому таку систему рівнянь слід розв'язувати числовими ітераційними методами. Для цього визначимо х1 з першого рівняння виразу (3.17), х2 — з другого, а х3 — з третього рівняння цієї системи
Нульове наближення х2(0) і х3(0) служить для визначення першого наближення х1(1) у відповідності з (3.22), яке використовується разом з х3(0) для знаходження x2(1) згідно з виразом (3.23), а х1(1) і х2(1) дають змогу розрахувати x3(1) за формулою (3.24). Ітераційний процес триває, поки х1, х2, х3 не вийдуть на усталені значення. Продемонструємо цей процес для попереднього прикладу (3.3), тільки при відомих а = 0,983075; b = 0,972458; с = 0,94194, a потрібно визначити х1, х2, х3. Результати розрахунків для торьох різних нульових наближень (х2(0) = х3(0) =0,6), (х2(0) = х3(0)=0,1), (х2(0) =0,8; х3(0) =0,9) наведені в таблиці 3.1. Таблиця 3.1
Ітерації 0 1 2 3 4 5 6 7 8 9 10 Невідомі x1 — 0,8687 0,7147 0,6886 0,6957 0,6957 0.6979 0,6990 0,6995 0,6998 0,6999 x2 0,6 0,8454 0.8166 0,8074 0,8074 0,8017 0,8008 0,8004 0,8002 0,8001 0,8000 х3 0,6 0.8343 0,8943 0,9009 0,9009 0,90050,9003 0,9001 0,900) 0,9000 0,9000 х1 — 0.9152 0,7493 0.6780 0,6823 0,6905 0.6953 0,6977 0,6989 0,6995 0,6997 х2 0.6 0,9185 0,8383 0,8160 0,8078 0,8038 0,8019 0,8009 0,8004 0.8002 0,8001 x3 0,6 0,7240 0,8817 0,9015 0,9020 0,90110.9006 0.90030,9001 0,9001 0,9000 х1 — 0,700 х2 0,8 0.800 x3 0,9 0,8343 Як видно з табл. 3.1, нульові наближення х2(0) і х3(0) впливають на обсяг і час обчислень. Чим вони ближчі до істинних значень, потрібна менша кількість ітерацій. У більшості випадків у складних логічних схемах елементи з'єднання «трикутника» і «зірки» поєднуються, тобто якщо є «трикутник», то можна виділити й «зірку». У зв'язку з тим, що еквівалентна заміна «трикутника» на «зірку» зведена до відомм аналітичних залежностей, рекомендується при розрахунку надійності системи проводити саме таку заміну.
Розділ 4. РОЗРАХУНОК НАДІЙНОСТІ РЕЗЕРВОВАНИХ СИСТЕМ БЕЗ ВІДНОВЛЕННЯ
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 (3.18)
(3.18)
 (3.22)
(3.22) (3.23)
(3.23)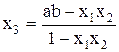 (3.24)
(3.24)


