
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логічне послідовне і паралельне з'єднанняСодержание книги Поиск на нашем сайте
У другому розділі в основному розглядалися теоретичні характеристики надійності окремих елементів, з яких формують системи. Тепер розглянемо розрахунок багатокомпонентних ситем — систем, елементи яких перебувають між собою в різноманітних логічних зв'язках. Одним з найбільш поширених таких логічних зв'язків нерезервованих систем є логічне послідовне з'єднання. Логічне послідовне з'єднання — це таке з'єднання, коли відмова хоча б одного елемента системи призводить до відмови системи в цілому. У цьому випадку час безвідмовної роботи системи дорівнює мінімальному значенню часу наробки до відмови елементів, з яких складається система. Логічна схема такого з'єднання показана на рис. 3.1.
рис.3.1.Логічна послідовна схема з¢єднання n елементів Якщо позначити ймовірність безвідмовної роботи і-го елемента системи 0 < Рі(t)< 1, то ймовірність P(t) безвідмовної роботи декількох логічно послідовно з'єднаних елементів згідно з теоремою множення дорівнює добутку ймовірностей безвідмовної роботи кожного елемента:
Очевидно, що чим більша кількість елементів, з'єднаних логічно послідовно, тим ймовірність безвідмовної роботи системи буде меншою. Наприклад, система з десяти послідовно з'єднаних однакових елементів, для яких Pj(tj) = 0,99 має ймовірність безвідмовної роботи Pc(tj) ==0,9, а для системи з двадцятьох таких елементів ймовірність безвідмовної роботи буде вже тільки 0,82. Приклад 3.1. Яку ймовірність безвідмовної роботи повинні мати елементи в певний момент часу, щоб ймовірність безвідмовної роботи системи, яка складається з шести таких компонентів, в той самий момент часу була не менше ніж 0,95. Розв'язування Pс(tj)>0,95. Оскільки Рc (tj) = Pj (tj)6, то Pj(tj) З урахуванням того, що
для ймовірності безвідмовної роботи при логічному послідовному з'єднанні отримаємо:
З виразу (3.4) напрошується такий висновок: Інтенсивність відмов декількох логічно послідовно з'єднання елементів L(t) дорівнює сумі інтенсивностей відмов всіх елементів.
Іншою логічною схемою з'єднань є логічно паралельне з'єднання. Логічне паралельне з'єднання — це таке логічне з'єднай елементів, при якому відмова будь.якого елемента не призводить до відмови всієї системи; система вийде з ладу тільки після відмови всіх елементів. Середній час наробки до відмови системи Тмс в цьому випадку дорівнює максимальному середньому часові наробки відмови Тi max елементів системи.
Рис.3.2. Логічна паралельна схема з'єднання п елементів. Ймовірність безвідмовної роботи при логічному паралельному з'єднанні будемо визначати виходячи з ймовірностей відмови одного елемента Qi(t)=1-Pi(t) (3.6) де Pi(t) — ймовірність безвідмов роботи одного елемента. Тоді ймовірність відмов кількох логічно паралельно з'єднаих елементів Q(t} дорівнює добутку ймовірностей відмов кожнoгo елемента Q(t)=Q1(t)×Q2(t)×...Qn(t)= З урахуванням (3.6) і (3.7) запишемо ймовірність безвідмовної роботи системи
Схема логічного Паралельного з'єднання показана на рис.3.2. Для n = 2 ймовірність безвідмовної роботи системи визначають як ймовірність того, що або перший, або другий елемент працездатний. Цій логічній функції згідно з (3.8) відповідає такий вираз: P(t)=1-[1-P1(t)][1-P2(t)]= P1(t)+ P2(t)- P1(t)P2(t) (3.9) Для n=3 ймовірність безвідмовної роботи системи знаходять як ймовірність того, що або перший, або другий, або третій елемент працездатний. Цій логічній функції відповідає такий вираз: P(t)=1-[1-P1(t)][1-P2(t)][1-P3(t)]= P1(t)+ P2(t)+ P3(t)- P1(t)P2(t)-P2(t)P3(t)- P1(t)P3(t)- -P1(t)P2(t) P3(t) (3.10) Аналогічним чином можна записати і для n = 4. P(t)=l-[l-P1(t)][l-P2(t)][l-P3(t)][l-P3(t)]= P1(t)+ P2(t)+ P3(t)+ P4(t)- P1(t)P2(t)- P2(t)P3(t)- - P3(t)P4(t)- P1(t)P3(t)- P2(t)P4(t)- P1(t)P4(t)+ P1(t)P2(t) P3(t)+ P1(t)P2(t) P4(t)+ + P1(t)P3(t) P4(t)+P2(t)P3(t) P4(t)- P1(t)P2(t) P3(t) P4(t) (3.11) 1-й працездатний
3-й працездатний
Рис.3.3. Діаграма для трьох паралельно з'єднаних елементів. З виразів (3.9)-(3.11) можна побачити закономірність, яка дає змогу записати P(t) для n алельно з'єднаних елементів. Надійність роботи системи при логічному паралельному з'єднанні елементів наочно ілюструє діаграма (рис.3.3).
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.13 (0.007 с.) |


 (3.1)
(3.1) Рc (tj)1/6=0.951/6=0.9915
Рc (tj)1/6=0.951/6=0.9915 (3.2)
(3.2)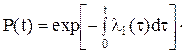
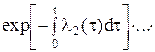
 (3.3)
(3.3) (3.4)
(3.4)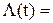 l1(t)+l2(t)+...+ln(t)=
l1(t)+l2(t)+...+ln(t)=  (3.5) З виразу (3.5) випливає, що l-характеристика системи, яка складається з послідовно з'єднаних елементів, визначається як сума ординат lі(t) характеристик всіх елементів.
(3.5) З виразу (3.5) випливає, що l-характеристика системи, яка складається з послідовно з'єднаних елементів, визначається як сума ординат lі(t) характеристик всіх елементів.
 (3.7)
(3.7)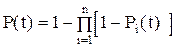 (3.8)
(3.8) 2-й працездатний
2-й працездатний


