
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Емпіричні залежності для оцінки надійностіСодержание книги Поиск на нашем сайте
Для кількісної оцінки надійності чи ненадійності роботи будь-якого виробу необхідно мати інформацію про поведінку цілої групи таких виробів, тобто простежити, як відмовляють елементи в часі. У цьому випадку можливі дві ситуації, які можна проілюструвати графіками (рис.2.1а і 2.16). Ці графіки представляють собою залежності кількості працездатних елементів в часі, тобто n(t) у вигляді гістограми (а) та її лінійної апроксимації (б), коли графік проходить через значення n(ti) на початку часового інтервалу.
Рис.2.1 Дискретна (гістограма) і неперервна (апроксимована) функції п(t).
З графіків 2.1 насамперед можна визначити функцію працездатності (надійності) P*(t)=n(t)/No. (2.1) де N„ — початкова кількість елементів. Очевидно, що Р*(0) = 1, а Р*(¥) = 0. Знайдемо кількість елементів, які вийшли з ладу (відмовили) за час D Dn = n(ti)-n(ti+Dt). (2.2) Тоді швидкість виходу з ладу визначимо як відношення Dn/Dt. Для отримання нормалізованої форми цієї швидкості (густини відмов) перейдемо до співвідношення
Зрозуміло, що така функція залежить від того, в якомумісціна осі часу розглядається інтервал Dt, і тому не може бути параметром надійності елемента. Цього можнo уникнути, якщо швидкість виходу з ладу елементів розділити на n(ti)
Характеристику, яку ми одержали, назвемо емпіричною інтенсивністю відмов, або емпіричною функцією азарту. Крім емпіричної функції надійності P*(t), широко використовується емпірична функція ненадійності (відмов) Q*(t)
Залежності (2.1)—(2.5) записані для випадку, коли n(t) зображено графіком на рис.2.1,а, до того ж D t = const на всьому часовому інтервалі. У випадку, коли n(t) зображено графіком на рис.2.1,6, емпіричну функцію надійності в будь-який момент часу розраховуємо за формулою
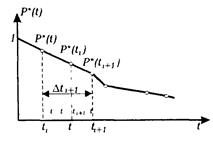
Графічний вираз (2.6) наведено на рис2.2., а функції f*(t) i l*(t) в цьому випадку набувають вигляду
Рис.2.2. Залежність емпіричної функції надійності від часу.
Величину n(t) розраховуємо за даними спостереження в моменти часу t ± ti+1 , між якими знаходиться час t, таким чином:
Ми розглянули випадки, коли Dt=const, або є змінним. У той же час можна Dt змінювати не довільно, а фіксувати інтервали часу, протягом якого відмовляє один елемент, тобто
У цьому випадку отримаємо:
2.2. Ймовірнісні характеристики надійності Для кількісної оцінки надійності функціонування неремонто-ваних виробів широко використовують характеристики та поняття, трактування яких запозичене з теорії ймовірності. Це пояснюється тим, що відмови мають випадковий характер, а тому описуються ймовірнісними залежностями. Отже, можна говорити про двояке трактування характеристик надійності: емпіричні, на основі статистичних досліджень, і теоретичні, які визначаються на основі постулатів теорії ймовірності. Останні дали змогу викристалізуватися теорії надійності в науку зі своїм специфічним апаратом досліджень. Як вже згадувалося, одним з основних показників надійності є ймовірність безвідмовної роботи виробу протягом заданого часу, інакше кажучи — це ймовірність того, що час Г безвідмовної роботи елемента чи системи буде більшим від заданого часу t, тобто P(t)=P{T>t}. (2.12) Аналогом цієї характеристики є функція працездатності P*(t), вираз (2.1) якої записаний в розділі 2.1. Ймовірність відмов Q(t) — це ймовірність того, що час Г безвідмовної роботи елемента чи системи буде меншим від заданого часу t, тобто Q(t)=P{T<t}. (2.13) Аналогом цієї характеристики є функція ненадійності Q*(t), яку описує вираз (2.5). Оскільки події «відмова» і «невідмова» утворюють повну групу подій, то P(t)+Q(t)=l. (2.14) Одним з недоліків показників P(t) і Q(t) є їхня залежність від часу. Тому ці характеристики здебільшого використовують для порівняльного аналізу надійності декількох виробів в один і той самий час, визначаючи коефіцієнт збільшення ймовірності безвідмовної роботи Sp=P1(ti)/P2(ti) (2.15) або коефіцієнт зменшення ймовірності відмов Sq=Q1(ti)/Q2(tI). (2.16) Для оцінки тенденції зміни функції Q(t)служить густина розподілу часу наробки до відмови f(t) (аналог — густина відмов f*(t)}. Традиційно густину функції відмов визначають f(t) == dQ(t)/dt, (2.17) причім
Ймовірність відмов в інтервалі часу t,...t, можна виразити через f(t) таким чином
або, якщо t1=0,a t2=t
Очевидно, що Q(0)=0,Q(¥)=1 (2.21) З виразу (2.21) на основі (2.14) випливає, що P(0) = 1, Р(¥) = 0. (2.22) Наступною характеристикою є функція, яку називають функцією азарту, або інтенсивністю відмов. Ми будемо користуватися останньою назвою. Інтенсивність відмов визначають як кількість відмов перемонтованого виробу з партії виробів в одиницю часу після даного моменту часу, за умови, що до цього моменту відмова не виникла. Розглянемо два інтервали часу на часовій осі. Перший (0,t) і другий (t, t+Dt).
____________ç_____Dt______ç_______________ 0 t t+Dt Час Для того, щоб якийсь елемент міг відмовити в інтервалі часу (t, t+Dt), він мусить безвідмовно попрацювати в інтервалі (0,t). Тому ймовірність відмови q(t, t+Dt) за час Dt згідно з правилом множення ймовірності q(t, t+Dt) =f(t)×dt=P(t)×Z(t) (2.23) де P(t) — ймовірність безвідмовної роботи елемента протягом інтервалу часу (0,t); Z(t) — умовна ймовірність відмови елемента за час (t, t+Dt), знайдена з урахуванням того, що елемент безвідмовно працював протягом часу (0,t). Нехай цю умовну ймовірність виражає формула Z(t)=l(t)dt, де l(t)-інтенсивність відмов. Враховуючи, що
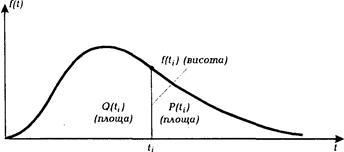
Проілюструємо взаємозв'язок між P(t), Q(t), f(t), l(t) на графіку (рис.2.3) залежності f(t)
Рис.2.3. Графічне зображення співвідношення між характеристиками (крива розподілу часу наробки до відмови). Інтенсивність відмов l(t) у відповідності з графіком рис.2.3 визначається як частка від ділення функції f(t) (висота) на площу, яка є праворуч від висоти. Графік f(t) називають кривою розподілу часу наробки до відмови. Якщо відома будь-яка функція з чотирьох f(t), Q(t), P(t) чи l(t), то три інші можна визначити. Доведемо це. Випадок 1. Відомо f(t). Знайдемо інші три функції:
Випадок. 2. Відомо Q(t). Знайдемо інші три функції: f(t) = dQ(t)/dt. (2.27) P(t)= l-Q(t). (2.28) l(t)==(dQ(t)/dt) ¤ l-Q(t). (2.29)
Випадок. 3.. Відомо P(t). Знайдемо інші три функції: Q(t) = l-P(t). (2.30) f(t)=-dP(t)/dt. (2.31)
Випадок 4. Відомо l(t}. Знайдемо інші три функції. Перейшовши до іншої змінної t, домножимо праву і ліву частини виразу (2.32.) на dt -l(t)×dt=dP(t)/P(t) (2.33) Проінтегруємо вираз (2.33) з межами інтегрування 0 ® t.
Враховуючи, що Р(0) = 1, запишемо InP(t)=- L(t) — сумарна (кумулятивна) функція інтенсивності відмов. Таким чином отримаємо:
Оскільки f(t) = l(t) P(f), то запишемо
Нарешті, ймовірність відмов може бути знайдена так:
Вирази (2.35), (2.36), (2.37) дають змогу знайти три функції через відому функцію інтенсивності відмов l(t). Доволі часто використовують таку характеристику, як середній час наробки до відмови Tм , який є математичним сподіванням часу наробки до відмови. У відповідності з визначенням математичного сподівання неперервної невід'ємної випадкової величини запишемо
Інтегруючи по частинах, отримаємо Tм=- Оскільки: - то
Таким чином, середній час наробки до відмови чисельно дорівнює площі під кривою P(t). У випадку, якщо l(t)=const, то з виразу (2.39) отримаємо
Підставивши в (2.35) значення t=Tм= 1/l, знайдемо, що середній час наробки до відмови можна розуміти як наробку t=Tм, протягом якої виріб залишається працездатним з ймовірністю P(Tм) = exp(-l) = 0,37. Для простих перемонтованих виробів, наприклад, елементів електронних схем, середня наробка до першої відмови є поняттям умовним, тому що переважно вони не експлуатуються так довго і старіють значно швидше, ніж встигають напрацювати Тм. Середній час наробки до відмови може бути визначений за статистичними даними як середньоарифметичне значення часу наробки до відмови виробів даної партиї (оцінка Тм по вибірці)
Незручність цієї формули полягає в тому, що необхідно знати часи виходу з ладу кожного з усіх виробів партії. За іншим способом визначають час tn, протягом якого виходять з ладу всі вироби даної партії, а також значення інтервалу часу Dt і кількість елементів Dm, які відмовили в цьому інтервалі. Тоді
де k=tn/Dt, tcepi=(t-i+1+ ti)/2 Для ремонтованих систем (систем з відновленням відповідними критеріями надійності [14] є: — ймовірність наробки між відмовами Р(Тз) більше заданого часу Тз; — параметр потоку відмов системи w(t); — наробка на відмову t н. Під наробкою на відмову розуміється середня тривалість, чи об'єм роботи системи між відмовами, які виникають послідовно. Величина Р(Тз) — це є ймовірність того, що наробка між відмовами tн буде більшою заданого часу Tз: P(Tз)=P{tн>Tз} (2.43) Цей показник є одним з найважливіших стосовно ремонтованих систем. Процес функціонування пристроїв складається з послідовності відмов, які відбуваються одна за одною у випадкові моменти часу за умови негайного відновлення. Важливим показником потоку відмов є параметр потоку, який визначається ймовірністю появи хоча б однієї відмови в одиницю часу після моменту t. Потік відмов елементів розглядається в таких системах, де ці елементи послідовно відмовляють. Мова йде про те, що елемент, який спочатку функціонував у системі, відмовив; його замінюють новим, який пізніше також відмовить, і т.д. Статистичне параметр потоку можна розрахувати як відношення середньої кількості відмов в одиницю часу m'(Dt)/Dt до загальної кількості позицій системи N', де ці елементи встановлені w*(t)= Потоки відмов елементів переважно є одинарними, тобто такими, в яких ймовірність появи в якийсь момент часу більше однієї відмови дуже мала і нею можна знехтувати. Потік відмов ремонтованої системи утворюється сукупністю одинарних потоків відмов елементів, що в неї входять, які розміщені на відповідних позиціях. Параметр потоку відмов такої ремонтованої системи W*(t) дорівнює сумі параметрів потоків w*(t) складових елементів, які розміщені на m* позиціях
Важливо відзначити, що в загальному випадку параметр потоку відмовw*(t) в тій позиції системи, де встановлено елемент, не дорівнює інтенсивності відмов l(t) цього елемента. Порівнюючи вираз для статистичного визначення інтенсивності відмовl*(t) і w*(t), видно, що ці характеристики є різними і збігаються тільки при l(t) = const. Зокрема, це слід мати на увазі при визначенні показників надійності за статистичними даними, які отримані в експлуатаційних умовах. Характер таких даних і способи їх обробки часто є такими, що фактично оцінюють параметри потоку відмов. Використання цих величин в ролі величин інтенсивностей відмов може призвести до значних похибок при розрахунку надійності. Потік відмов називається стаціонарним, якщо ймовірність появи якоїсь кількості відмов в інтервалі часу t... (t+Dt) залежить тільки від Dt і не залежить від t. Параметр стаціонарного потоку є постійною величиною. Для елемента, який встановлений в i—тій позиції системи, він дорівнює величині, оберненій значенню середнього часу Тim наробки до відмови елемента:
Важливою властивістю потоку відмов є його наслідки. Відсутність наслідків означає, що відмови є випадковими і незалежними однієї події від іншої. Потік відмов, якому одночасно властива одинарність, стаціонарність і відсутність наслідків, називається простим (або пуассонівським) потоком. Поширеним показником надійності ремонтованих систем є наробка до відмови Tн. Якщо відома густина ймовірності часу між відмовами j(tн) то Tн може бути визначено так:
В усталеному режимі роботи системи, коли W*(t)
Ремонтовані системи характеризуються також показниками ремонтопридатності. Показником ремонтопридатності є ймовірність P(t зв) відновлення системи за заданий час tв і середній час відновлення Тв. Якщо густина ймовірності відновлення системи визначається функцією f(tв), то ймовірність відновлення за час tв дорівнюватиме
а середній час відновлення буде
Середній час відновлення показує середні затрати часу на виявлення і ліквідацію відмови при деяких заданих умовах роботи. Крім розглянутих показників надійності ремонтованих систем, існують ще й інші, а саме: функція готовності і простою, коефіцієнти готовності і простою. Ці показники більш детально розглядаються в § 5.2. Очевидно, що показники надійності як перемонтованих, так і ремонтованих пристроїв і систем є різноманітними, але між ними існують певні зв'язки. Тому при аналізі надійності слід використовувати не всі показники, а вибирати ті, які найповніше характеризують надійність, і до кожного випадку підходити індивідуально.
Закони розподілу У розділі 2.2 введено поняття «крива розподілу часу наробки до відмови», тобто залежність f(t). Ця залежність може служити математичною моделлю надійності виробу, необхідною для теоретичної оцінки надійності окремого елемента чи системи в цілому. Зрозуміло, що спектр різновидів функцій f(t) буде дуже широким, оскільки вони відбивають особливості фізичних процесів, властивих саме тому чи іншому виробові. Маючи криву розподілу наробки до відмови, визначають всі інші характеристики надійності. З урахуванням (2.18) можна стверджувати, що кривою розподілу може бути будь-яка лінія, площа під якою дорівнює одиниці. Як свідчать численні дослідження, надійність більшості виробів може бути змодельована певною сукупністю функцій, які ми розглянемо далі. Вони дають змогу описати величину f(t) з максимальним наближенням до тих залежностей f'(t), які відбивають реальну природу виробів. Це є розподіли Вейбула, гама-розподіл та їх окремі випадки, якими дуже часто користуються, нормальний розподіл, логарифмічно-нормальний, альфа-розподіл, розподіл Релея, трикутний розподіл тощо. Коротке пояснення аналітичних виразів законів розподілів і області їх застосування в теорії надійності почнемо з розподілу Вейбула [З]. У цьому випадку
де С — параметр масштабу, який «стискає», чи «розтягує» криву; b — параметр форми розподілу, який стискає його асиметрію і ексцес. Графіки функції розподілу Вейбула показані на рис.2.4. Запишемо ймовірність безвідмовної роботи для даного випадку
Рис.2.4. Графіки розподілу Вейбула при С=1 у випадках b = 0,5 (крива 1), b = 1 (крива 2), b = 1.5 (крива 3), b = 2 (крива 4), b = 4 (крива 5). Своєю чергою інтенсивність відмов матиме вигляд:
Вирази (2.52) і (2.53) графічно зображені на рис.2.5.
Рис.2.5. Криві інтенсивності відмов та ймовірності безвідмовної роботи при розподілі Вейбула. Середній час наробки до відмови Тм розраховують таким чином:
де Розподіл Вейбула використовують для отримання математичної моделі надійності деякого механічного обладнання, зокрема, підшипників, які застосовують в електричних двигунах, а також для окремих типів електронних ламп (р= 1,4¸1,7). Перевагою розподілу Вейбула є велика кількість форм кривих, які можна отримати. Це дає змогу використовувати даний закон розподілу для більш широкого класу електрооб- ладнання, ніж вказано вище, в початковий період експлуатації (період приробки). Наступною моделлю густини розподілу часу наробки до відмови є гама-розподіл. У цьому випадку згадана густина розподілу має вигляд:
Такий розподіл також задається двома параметрами: b — параметр масштабу; a — параметр форми розподілу. Графічне зображення f(t) для гама-розподілу показано на рис.2.11. Середній час наробки до відмов у цьому випадку визначають як TM =a/b. У теорії надійності гама-розподіл використовується при цілих значеннях a. Тоді гама-розподіл називається розподілом Ерланга [4]. Для розподілу Ерланга запишемо
Ймовірність безвідмовної роботи та інтенсивність відмов матиме вигляд
Рис. 2.6. Гама-розподіл при різних параметрах a.
Графіки залежностей f(t),P(t),l(t) для розподилу Ерланга показані нав рис.2.7
Рис.2.7. Графіки функцій при розподілі Ерланга (l>1). Розподіл Ерланга другого порядку (b = 1, l = 2/Тв) широко використовують для моделювання розподілу часу відновлення систем електроприводів. Це пояснюється тим, що час відновлення tв складається з двох частин: tВ=to+tp (2.59) де to — час, затрачений на пошук несправностей; tp — час, затрачений на ремонт. Якщо припустити, що випадкові величини to і tp розподілені за експоненційним законом ((2.62) — (2.64)) з однаковими середніми значеннями ТB/2, то густина ймовірності величини tB, яка є комбінацією to і tp відповідності з відомими положеннями теорії ймовірності:
Залежність f(tB), побудована у відповідності з (2.60), відповідає графіку на рис.2.12 при l > 1, тобто має вигляд густини розподілу Ерланга. Критерій ремонтопридатності — ймовірність відновлення системи за tзв буде у відповідності з (2.49) дорівнювати:
Гама-розподіл також має великий спектр кривих. Особливістю такого розподілу є те, що сума n незалежних випадкових величин, кожна з яких підпорядковується гамарозподілу з параметрами a і b,також має гама-розподіл з параметрами b і Розглянемо окремий випадок розподілу Вейбула (при a = 1) та гама-розподілу Ерланга (при b =1) — експоненційний розподіл. Цей розподіл часу наробки до відмови характеризується виразами f(t), P(t), l(t). l(t) = l = const, (2.62) f(t)=l exp(-lt), (2.63) P(t)=exp(-lt). (2.64) Такий закон розподілу ще називають показниковим. Графіки функцій f(t), l(t) і P(t) при експоненційному законі розподілу показані на рис.2.8. .
Рис2.8. Графіки екпоненціального закону росподілу. Наведений закон розподілу використовують доволі часто, оскільки він придатний для опису характеристик надійності склад них електромеханічних систем, навіть якщо елементи цих систем мають різноманітні закони розподілу. Це пояснюється тим, що більшість виробів проходить «тренування» безпосередньо після виготовлення в заводських умовах і до споживача вони надходять при стабільно низьких значеннях інтенсивностей відмов. Завдяки цьому споживач працює з виробами, які мають більш-менш постійні величини l. Експоненційний розподіл також набув широкого поширення через простоту формул для розрахунку характе ристик надійності. При недостатній кількості статистичних дант складно виявити відхилення від виразу l = const, навіть якщо такі відхилення і відбувається. У цьому випадку постійне значення інтенсивності відмов можна прийняти як перше наближення при розрахунках. У той же час, якщо вироби не пройшли «тренування»на виробництві в початковий період експлуатації, розподіл часу наробки до відмови потребує іншої математичної моделі. Такою моделлю може бути нормальний закон розполілу. Цей розподіл ще називають розподілом Гаусса. Оскільки час наробки до відмови набуває тільки додатних значень, то в теорії надійності йдеться про зрізаний нормальний розподіл. Зрізаний нормальний розподіл отримують з нормального, обмежуючи інтервал значень випадкової величини часу наробки до відмови t1 ¸ t2. Тоді запишемо густину зрізаного нормального розподілу f(t)=C· f(t), (2.65) де С — нормуючий множник, який забезпечує нормування кривої розподілу, тобто
Підставимо в (2.66) вираз для f(t) і, застосувавши позначення
де TM- середній час наробки до відмови; s— середнє квадратичне відхилення часу наробки до відмови для незрізаного розподілу, після перетворень отримаємо:
де Таблиця значень цієї функції наведена в додатку 2. У випадку 0 < t < ¥ (а саме цій умові відповідає зрізаний нормальний розподіл) отримаємо такі вирази для функцій: а) де б) в) г) де
На рис. 2.9 наведені залежності відношення числових характеристик зрізаного і незрізаного нормального розподілу і значені нормуючого множника С від співвідношення Тм /s.
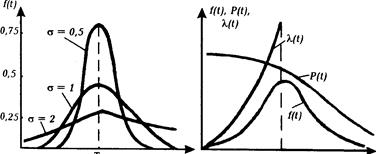
Рис.2.9. Залежність відношення числових характеристик зрізаного і незрізаного нормального розподілу (риска над Як видно з рис.2.9. при Графічне зображення f(t), l(t), P(t) для зрізаного розподілу показано на рис.2.10.
Рис.2.10. Функціональні залежності при нормальному законі розподілу. Необхідно відзначити, що умовою нормального розподіл наробки до відмови є малий розкид значень швидкостей зношування елементів, тому що саме поява відмов за рахунок зношування елементів найкраще моделюється нормальним законом розподілу. Бувають випадки явно несиметричних розподілів часу наробки до відмови. Тоді за модель f(t) беруть логарифмічний нормальний закон розподілу. Логарифмічний нормальний (логнормальний) розподіл задається густиною розподіл
де m — середнє значення випадкової величини t; s — середньоквадратичне відхилення величини ln t. Ймовірність безвідмовної роботи розраховують за такої формулою [14].
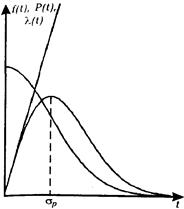
Рис.2.11. Криві густини при логарифмічному нормальному законі розподілу. Криві густини логнормальног розподілу наведені на рис.2.11. Дослідження, виконані в роботі [14] показують, що логнормальний закон розподілу часу відновлення (ремонту) характерний для випадків, коли системі керування електроприводами ремонтують, замінюючи несправні елементи, безпосередньо на міці де працює електропривод. Якщо у час відновлення входить такоз час пошуку несправностей і безпосередньо ремонт, то кращою математичною моделлю є окремий випадок — розподіл Ерланга другого порядку. Розглянемо ще декілька законів розподілу, які можуть використовуватись для побудови математичних моделей надійності. Розполіл Релея описують виразами [4];
Рис.2.12. Графічні залежності розподілу Релея.
f(t)=t/s2exp[-t2/(2sp2)] (2.75)
де sр — параметр розподілу Релея, який є модою розподілу (значення t, яке відповідає екстремуму функції) і його не слід плутати зі середньоквадратичним відхиленням. Для розподілу Релея математичне сподівання (середній час наробки до відмови)
а дисперсія
Графіки функцій розподілу Релея показані на рис.2.12. Трикутний розподіл характеризує випадкові величини, які мають обмежену область можливих значень (tn, tk) Цей розподіл (рис.2.13) описують такі три параметри: tn, tk — межі допустимих значень, tm — мода. Якщо позначити f(tm)= h то з визначення площі трикутника отримаємо: 0.5h(tn- tk)=1 (2.80) З виразу (2.80) отримаємо h=2/(tn- tk) (2.81)
Puc.2.13. Графічні залежності при трикутному розподілі. Тоді запишемо густину розподілу f(t) з урахуванням (2.81) Ймовірність безвідмовної роботи матиме вигляд:
Інтенсивність відмов для трикутного розподілу буде такою:
Біноміальний розподіл. Цей дискретний розподіл описує появу подій, які мають два значення, що взаємно виключають одне одного. Якщо, наприклад, в партії із 100 виробів 90 справних, а 10 бракованих, то ймовірність появи цих виробів становить 0,9 справних і 0,1 — бракованих. Очевидно, що коли в певну сукупність однакових виробів входять справні вироби, відносна частка яких становить р і браковані, відносна частка яких становить q, то p+q=l. Якщо з великої партії однакових виробів з q % несправних, береться вибірка в кількості n, то ймовірності появи різної кількості несправних виробів в цих вибірках визначаються коефіцієнтами розкладання членів біноміального ряду (Р + q)n =1 або
де q=q%/100% — частка одиниці несправних виробів в партії, а р — частка справних. У рівнянні (2.85) рn показує ймовірність відсутності несправних виробів у вибірці об'ємом n зразків, другий член npn-1q дає ймовірність появи у вибірці одного несправного виробу, третій член Приклад 2.1. З великої партії сельсинів типу НС-404, в якій є q % =5% несправних зразків, береться для використання в системі вибірка з чотирьох машин (n=4). Визначити ймовірність появи у вибірках О, 1, 2, 3 чи 4 несправних сельсини. Розв'язування.
Тоді ймовірність появи у вибірці 0 несправних сельсинів: p4=(0.95)4=0.8145. Ймовірність появи у вибірці 1 несправного сельсина: 4pзq=4×(0,95)3×0,05=0,1715. Ймовірність появи у вибірці 2 несправних сельсинів: 6p2q2=6×(0.95)2×(0.05)2=0.0136. Ймовірність появи у вибірці 3 несправних сельсинів: 4pqз=4×(0,95)×(0,05)3=0,0004. Ймовірність появи у вибірці 4 несправних сельсинів: q4=(0,05)4=0,0000. Повна ймовірність дорівнює 1,000. Розподіл Пуассона. У випадку дискретного розподілу Пуассона розглядають події, ізольовані в часі чи просторі. Так, кількість відмов у роботі якоїсь системи протягом деякого проміжку часу характеризує появу ізольованих в часі подій. Розподіл Пуассона, як і біноміальний, також складається з ряду членів, кожен з яких відповідно визначає ймовірність появи О, 1, 2, 3 чи більшої кількості подій на одиницю вимірювання. При цьому сума цих ймовірностей дорівнює одиниці. Розподіл Пуассона записують таким чином
де а- середня кількість несправних виробів, або несправностей на вибір при вибірці об¢ємом n. Величина а визначається як добуток об¢єму вибірки n на середнє значення частки кількості несправностей на вибір,або частки несправних виробів у цілій партії q¢,тобто ф=nq¢ при цьому
або
У виразі (2.86) кожен член лівої частини означає: e-a - ймовірність появи 0 несправностей на виріб, або несправних виробів у вибірці; ae-a - ймовірність появи 1 несправності на вибір, або несправного виpобу у вибірці;
Розподіл Пуассона зручно використовувати, наприклад, при контролі якості виробів. Він визначає основу для складання плану вибіркового прийому виробів у відділах технічного контролю підприємства. Розподіл Пуассона при Ь = 0 і a =lt перетворюється в експоненційний закон розподілу. Отже, експоненційний закон розподілу є окремим випадком закону розподілу Пуассона. Лямбда-характеристика У розділі 2.3 розглянуто різноманітні математичні моделі надійності. Завданням дослідника є підбір такого закону розподілу, який би забезпечував адекватність моделі процесам відмови виробу. У той же час можливі ситуації, коли експериментальні залежності f(t),l(t) не підпадають ні під один відомий закон розподілу протягом часу функціонування системи чи окремого елемента. Тоді користуються експериментальними кривими, зокрема, залежністю інтенсивності відмов від часу, для оперативного прийняття рішень з підвищення надійності. Така залежність називається лямбда-характеристикою (l-характеристика). Лямбда-характеристика дає змогу виявити деякі особливості і недоліки експлуатації технічних пристроїв, тобто вона вказує на необхідність проведення тих чи інших заходів щодо забезпечення потрібного рівня надійності. Типова l-характеристика показана на рис.2.14. Можна відзначити три характерні її ділянки: І — період припрацьовування з високим рівнем інтенсивності відмов, коли очевидно ненадійні елементи (або елементи з прихованими дефектами) швидко відмовляють; II — період нормальної роботи, коли на інтенсивність відмов впливають різноманітні випадкові чинники, але сама інтенсивність відмов залишається постійною і мінімальною; III — період старіння, під час якого лавиноподібне зростає інтенсивність відмов, і зумовлений цей процес зношуванням та старінням елементів.
Рис.2.14. Типова l-характеристика. За аналогією з життям людини напрошуються такі визначення періодів l-характеристики: І — «дитинство», II — «зрілість», і — «старість». З точки зору забезпечення надійної роботи вироб необхідно його експлуатувати в період «зрілості». Для забезпечеі ня тривалішого цього періоду необхідно скоротити період «дитинства». Цього досягають шляхом припрацювання і тренуванн пристроїв на заводі в умовах, близьких до експлуатаційних. Швидкість переходу з періоду І в період II може служти опосередкованим показником культури виробництва. Чим вища якість виготовлення і перевірки елементів, тим більш однорідною є продукція, і тим швидше падає інтенсивність відмов, зумовлені виробничими причинами (поганий монтаж, неякісне лютування тощо). При погіршенні якості виготовлення пристрою період «дитинства» збільшується і перехід до періоду II стає дуже плавним. При цьому «тренування» часто стає нераціональним. Необхідно відзначити, що l-характеристики систем не завжди мають такий вигляд, як на рис.2.14. Вони можуть відрізнятися від наведеної кривої тому, що складові систем мають різну механічі і електричну міцність та різні l-характеристики. Цим зумовлена поява локальних екстремумів (максимумів) на характеристиці наприклад, як це пок
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.78.12 (0.017 с.) |


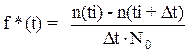 . (2.3)
. (2.3) . (2.4)
. (2.4) . (2.5)
. (2.5)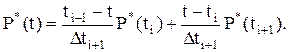 (2.6)
(2.6)
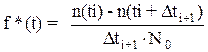 . (2.7)
. (2.7) . (2.8)
. (2.8)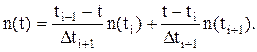 (2.9)
(2.9) . (2.10)
. (2.10)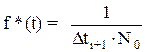 ti<t<ti+1
ti<t<ti+1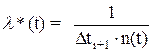 ti<t<ti+1. (2.11)
ti<t<ti+1. (2.11)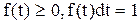 (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20)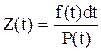 ,знайдемо
,знайдемо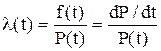 .
.
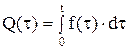 . (2.24)
. (2.24) . (2.25)
. (2.25)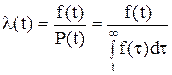 . (2.26)
. (2.26)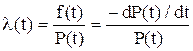 . (2.32)
. (2.32) . (2.34)
. (2.34) .
.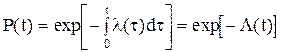 (2.35)
(2.35)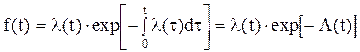 (2.36)
(2.36) (2.37)
(2.37)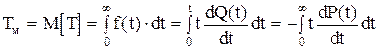 . (2.38)
. (2.38)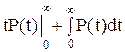 .
.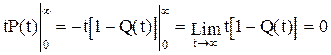 ,
,  . (2.39)
. (2.39)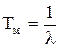 (2.40)
(2.40)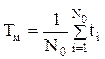 . (2.41)
. (2.41) . (2.42)
. (2.42)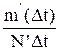 . (2.44)
. (2.44) . (2.45)
. (2.45) . (2.46)
. (2.46)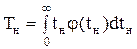 (2.47)
(2.47) . (2.48)
. (2.48)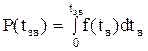 (2.49)
(2.49)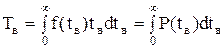 (2.50)
(2.50)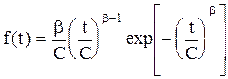 (2.51)
(2.51)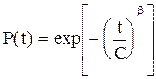 (2.52)
(2.52)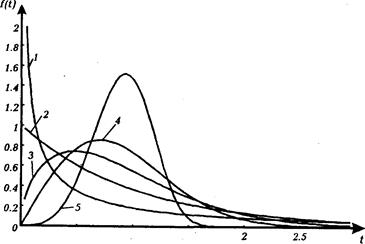
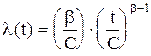 (2.53)
(2.53)
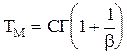 (2.54)
(2.54) - гама-функція, яку знаходять за таблицями в додатку 1.
- гама-функція, яку знаходять за таблицями в додатку 1.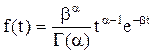 , a,b >0, t>0 (2.55)
, a,b >0, t>0 (2.55) (2.56)
(2.56)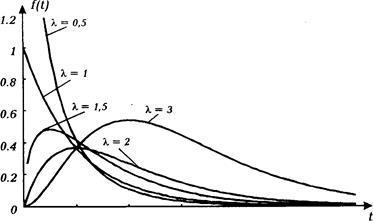
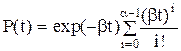 (2.57)
(2.57) (2.58)
(2.58)
 (2.60)
(2.60) (2.61)
(2.61)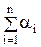

 - густина нормального розподілу;
- густина нормального розподілу; , звідки
, звідки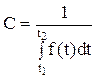 (2.66)
(2.66)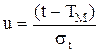 ,
, (2.67)
(2.67) — нормальна функція Лапласа.
— нормальна функція Лапласа.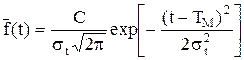 (2.66)
(2.66)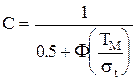
 (2.69)
(2.69) (2.70)
(2.70)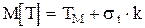 (2.71)
(2.71)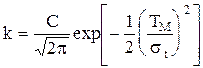
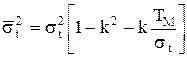 (2.72)
(2.72)
 і
і 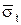 означає, що ці характеристики належать до зрізаного розподілу).
означає, що ці характеристики належать до зрізаного розподілу).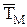 /
/ 
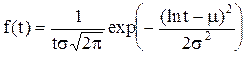 (2.73)
(2.73)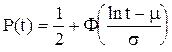 (2.74)
(2.74)
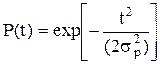 (2.76)
(2.76)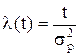 (2.77)
(2.77) (2.78)
(2.78)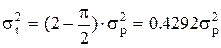 (2.79)
(2.79)
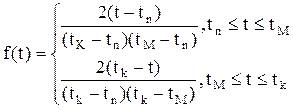 (2.82)
(2.82)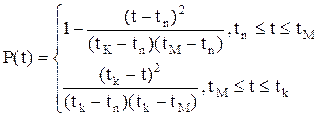 (2.83)
(2.83)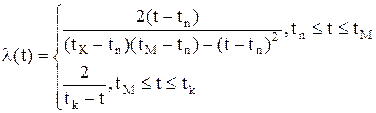 (2.84)
(2.84) — ймовірність появи у вибірці двох несправних виробів тощо, останній член qn визначає ймовірність появи у вибірці n несправних елементів.
— ймовірність появи у вибірці двох несправних виробів тощо, останній член qn визначає ймовірність появи у вибірці n несправних елементів.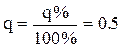 ; q =1-0.05 = 0.95. При цьому (p+q)4= 1.
; q =1-0.05 = 0.95. При цьому (p+q)4= 1. (2.86)
(2.86)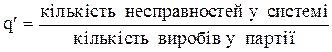
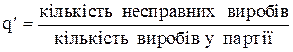
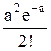 -ймовірність появи 2 несправностей на вибір, або двох несправних виробів у вибірці;
-ймовірність появи 2 несправностей на вибір, або двох несправних виробів у вибірці;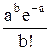 - ймовірність появи Ь несправностей на виріб, або b несправних виробів у вибірці.
- ймовірність появи Ь несправностей на виріб, або b несправних виробів у вибірці.






 t t
t t


