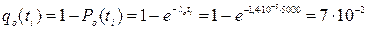Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пасивне резервування з дробовою кратністюСодержание книги Поиск на нашем сайте
Схема резервування з дробовою кратністю показана на рис.4.2,д, е, ж, з. Такого вигляду схеми використовують в основному при пасивному резервуванні. Нехай функціональний вузол системи складається з l логічно паралельно з'єднаних блоків. Для нормальної роботи системи необхідно, щоб справними були не менш ніж h блоків. Тоді ймовірність безвідмовної роботи визначається виразом, який отриманий на основі логіко-ймовірнісного методу
де Враховуючи, що інтенсивність відмов блока L*, можемо записати
Для аналізу ефективності резервування розглянемо випадок коли r = 1/2. Нехай l = 3; h = 2. З виразу (4.27) отримаємо
Побудуємо залежність Р =f(L*t) (рис.4.4).
Рис.4.4. Залежність Р(L* t) при r=0 i r=1/2 Для порівняння там же показана залежність для r = О (пункті на лінія). З графіка видно, що дробова кратність дає збільшення надійності тільки до певного з чення L*t<ln2 (4.30) для випадку r = 1/2. Із збільшенням кратності резервування область значеньL*t, при яких доцільно використовувати такі схеми збільшується. Отже, резервування з дробовою кратністю доцільно використовувати в системах з короткочасним режимом роботи. 4.2.5. Резервування елементів з двома типами відмов Більшість елементів різноманітних систем, зокрема, ектромеханічних, мають відмови двох типів. Це відмови, зумовлені обривом, або коротким замиканням в елементі. Такі відмови властиві конденсаторам, вентилям, резисторам, контактним елементам тощо. Для механічного обладнання — це відмови, спричинені проковзуванням чи заклинюванням. Позначивши ймовірність відмов, які зумовлені обривом через q0(t), а ймовірність від викликаних коротким замиканням, qs(t) отримаємо P(t)+q0(t)+qs(t)=l (4.31) де P(t) — ймовірність безвідмовної роботи елемента. Вираз (4.31) випливає з того, що події працездатності і відмов утворюють повну групу подій. Повна ймовірність відмов елемента Qе(t) дорівнює
Досить часто значення q0(t) і qs(t) виражають через Qе(t) за допомогою вагових коефіцієнтів a і b. Тобто q0(t)=a Qе(t) (4.33) qs(t)=b Qе(t) (4.34) Очевидно, що a+b= 1 (4.35) Підвищити надійність роботи елемента можна зменшуючи ймовірності відмов обох типів. Покажемо це, вважаючи спочатку що елемент може відмовити тільки внаслідок обриву. Тоді для підвищення надійності слід під'єднати паралельно йому ще такий самий елемент. Ймовірність відмов такої схеми
Розглянемо другий випадок, коли елемент може мати тільки коротке замикання. Тоді для підвищення його надійності послідовно з ним під'єднати ще один елемент. Ймовірність відмов
Отже, якщо елемент має тільки обрив, чи тільки коротке замикання, то підвищення надійності досягається резервуванням, яке полягає в паралельному під'єднанні резервних елементів, чї послідовному з'єднанні з основним. Проаналізуємо зміну ймовірності відмови елементів при паралельному і послідовному з'єднанні елементів, якщо для них властиві відмови двох типів. При паралельному з'єднанні, зумовленому резервуванням обриву, поява короткого замикання підпорядковується логічній послідовній схемі з'єднання. Тому отримаємо
Повну ймовірність відмов запишемо
З урахуванням (4.33) і (4.34) з виразу (4.39) отримаємо
Доцільність резервування визначається нерівністю
На рис.4.5 показані залежності
Рис.4.5. Залежність ймовірності відмови системи від Як видно з наведених графіків, надійність такої резервованої системи підвищиться тільки при a > 0,5, тобто коли
Розглянемо тепер випадок послідовного з'єднання елементів для здійснення резервування за коротким замиканням. При такому резервуванні ймовірність відмов, зумовлених обривом, визначається за правилом логічного послідовного з'єднання.
Повна ймовірність при послідовному з'єднанні елементів
Після здійснення побудови Qпос (t) = f [Qe (t)] на рис.4.6можна зробити висновок, що таке резервування має сенс тільки при a<0,5[q0(t)<qs(t)].
Рис.4.6. Залежність Qпос (t) = f [Qe (t)] для двох послідовно з'єднаних елементів. Проведені дослідження резервованих схем з кількістюрезервних елементів 2,3 і більше показали, що результат мало відрізняється від отриманих значень для одного резервного елемента (крім крайніх випадків a = 0 і a = 1, але це означає, що елемент має тільки один тип відмов). Розглянемо випадок, коли q0(t) і qs(t) мало відрізняю тобто a» 0,5. Саме тоді під'єднання або послідовно, або паралельно резервного елемента не дає відчутного ефекту. В цьому випадку використовується для резервування і послідовне, і паралельне з'єднання, які показані на рис.4.7. Таке з'єднання називається елементарною резервова ланкою. Для таких схем ймовірність Qс(t) визначається двома складовими:
де Qoc (t) — ймовірність відмов системи, зумовлена тільки обривами; Qsc(t)— ймовірність відмов системи зумовлена тільки короткими замиканнями.
а), б). Рис.4.7. Схеми резервування елемента з двома типами відмов. Для схеми на рис.4.7,а отримаємо
Остаточно отримаємо
У випадку qs = q0 отримаємо
Розглянемо тепер розрахунок надійності для схеми на рис.4.7,6.
Отже,
У випадку qs == q0 отримаємо
Вирази (4.48) і (4.52) доказують, що при qs = q0 обидві схеми йа рис.4.7,а і рис.4.7,6 рівнонадійні.
В електричній схемі релейні контактні пари так, як показано на рисунку
. Розв'язування
Оскільки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 (4.27)
(4.27) і
і  відповідні поєднання чисел;P0(t)— ймовірність безвідмовної роботи блока.
відповідні поєднання чисел;P0(t)— ймовірність безвідмовної роботи блока. (4.28)
(4.28)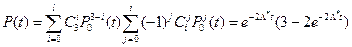
 (4.29)
(4.29)
 . Це означає, що таке резервування має сенс тільки тоді коли L*t менше якогось критичного значення Виконані досліди показали [14], що це критичне значення визначається нерівністю
. Це означає, що таке резервування має сенс тільки тоді коли L*t менше якогось критичного значення Виконані досліди показали [14], що це критичне значення визначається нерівністю (4.32)
(4.32) (t) буде:
(t) буде: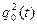 (4.36)
(4.36) такої схеми матиме вигляд:
такої схеми матиме вигляд: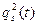 (4.37)
(4.37)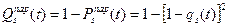 (4.38)
(4.38) (4.39)
(4.39) (4.40)
(4.40) (4.41)
(4.41) від
від  .
.

 (4.42)
(4.42) (4.43)
(4.43)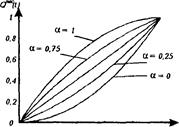
 (4.44)
(4.44)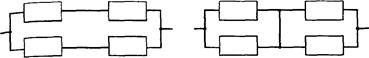
 (4.45)
(4.45) (4.46)
(4.46) (4.47)
(4.47) (4.48)
(4.48) (4.49)
(4.49)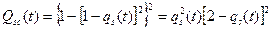 (4.50)
(4.50) (4.51)
(4.51) (4.52)
(4.52)